以下为个人学习笔记整理，源项目 github 链接。

# SoloMesh

SoloMesh 的构建过程可以分为如下几步：

「Step 1」Initialize build config
「Step 2」Rasterize input polygon soup
「Step 3」Filter walkables surfaces
「Step 4」Partition walkable surface to simple regions
「Step 5」Trace and simplify region contours
「Step 6」Build polygons mesh from contours
「Step 7」Create detail mesh which allows to access approximate height on each polygon
「Step 8」Create Detour data from Recast poly mesh

# Initialize build config

可以设置的参数介绍：相关参数介绍

# Rasterization

用于设置体素化 AABB 的粒度

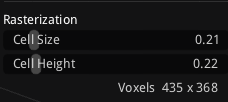
# CellSize

Cell 的长宽（xz-plane）

# CellHeight

Cell 的高（y）

# Voxels

根据「CellSize」能够把地图切分成的 width x height 数量。

# Agent

用于限制某块区域的可行走状态

# Height

行走对象的高度

# Radius

行走对象的步长半径

# MaxClimb

行走对象的最大爬坡高度

# MaxSlop

行走对象的最大爬坡角度

# Region

控制组成单个行走区域的范围大小

# MinRegionSize

「Region」的最小尺寸，小于该值则不会算作一个「Region」

# MergedRegionSize

「Region」的最小合并尺寸，小于该值会被合并。

# Partioning

控制「Region」生存所用算法

三种分区算法

Watershed：分水岭算法
Monotone：单调分割算法
Layers：分层算法

# Filtering

一些可选的剔除 or 过滤项

Low Hanging Obstacles：考虑是否计算可以攀爬的「Span」。
Ledge Spans：「Ledge」被解释为墙壁或者垂直的障碍物，开启该功能后会在「Ledge」周围扩展一定范围作为不可行走区域。
Walkable Low Height Spans：开启后会剔除接近「行走对象高度」的「Spans」区域。

# Polygonization

控制「Region」转到「Poly」时的切分规则

# MaxEdgeLength

多边形面片的最大边长，超过则会进行拆分。

# MaxEdgeError

面片和几何物体的距离，可以理解为面片和几何的贴合程度，越小贴合越紧密，面片越多。

# VertsPerPoly

多边形的最大顶点数。

# Detail Mesh

控制「Poly」内部的细分规则

# SampleDistance

网格采样距离，用于对「Poly」进行进一步的细分，越小切分的网格越多，该参数受到「MaxSampleError」影响。

# MaxSampleError

网格和几何物体的距离，越小网格越贴合物体表面。

# ConvexVolumeTool 相关配置

标识需要包含和排除的地形类型

# AreaType

# Rasterize input polygon soup

场景体素化，把顶点坐标等模型数据转化为单位立方体（体素）。

「Step.1」：标记满足爬坡角度 MaxClimb 的三角形，用于过滤不可行走区域

	// rcMarkWalkableTriangles
	for (int i = 0; i < nt; ++i) //nt 三角形数量
	{
	const int* tri = &tris[i*3]; //tris 三个为一组，记录三角形顶点编号
	calcTriNormal(&verts[tri[0]3], &verts[tri[1]3], &verts[tri[2]*3], norm);
	// Check if the face is walkable.
	if (norm[1] > walkableThr)
	areas[i] = RC_WALKABLE_AREA; // RC_WALKABLE_AREA = 0x3f
	}

# RasterizeTriangles

「Step.2」体素化三角形

计算所有三角形各自的「AABB」包围盒，用于过滤越界的三角形

	float tmin[3], tmax[3];
	// Calculate the bounding box of the triangle.
	rcVcopy(tmin, v0);
	rcVcopy(tmax, v0);
	rcVmin(tmin, v1);
	rcVmin(tmin, v2);
	rcVmax(tmax, v1);
	rcVmax(tmax, v2);

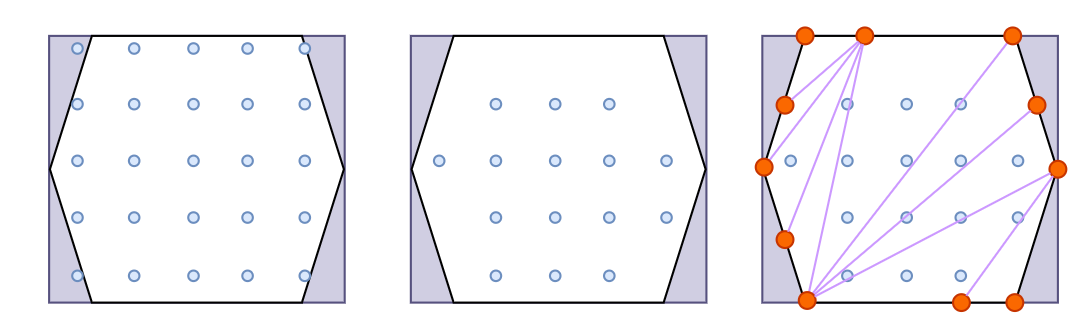
对三角形进行切割 ——DividePoly

# DividePoly

「Step.2.1」：以 xz-plane 按照「CellSize」生成网格，并按照先 x 后 z 进行切割

	// divides a convex polygons into two convex polygons on both sides of a line
	static void dividePoly(const float* in, int nin,
	float* out1, int* nout1,
	float* out2, int* nout2,
	float x, int axis)

in：输入三角形顶点。
out1、out2：输出切割后轴两边的顶点，并作为下一次输入

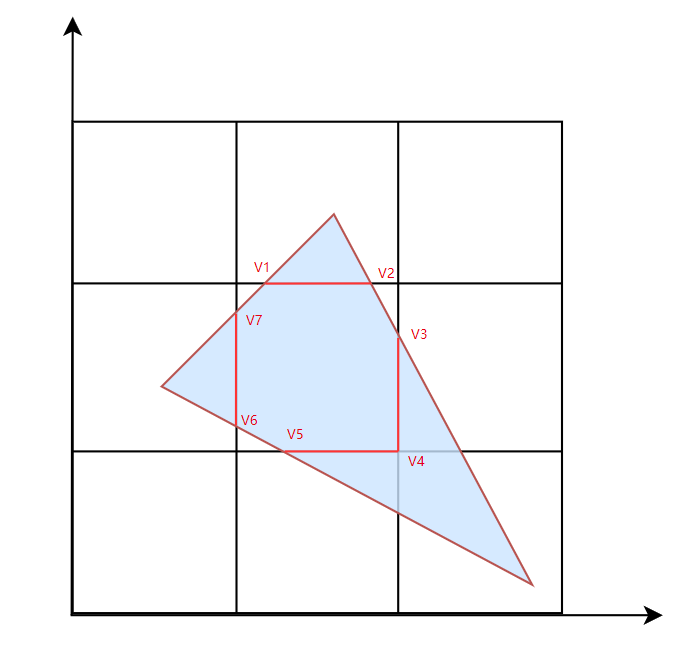
	// Clip the triangle into all grid cells it touches.
	// \|_______\|_______\|_______\|_______\| 7 x 3 x 4
	// in inrow p1 p2
	// 运行过程中，这几个指针会不停的交换指向，来变更三角形输入和输出位置，看着相当之头大
	float buf[734];
	float in = buf, inrow = buf+73, p1 = inrow+73, p2 = p1+7*3;

存储切割结果的数据结构 7 x 3 x 4。
7：对三角形进行切割的时候，最多会产生 7 个顶点的多边形。

3：顶点坐标 x,y,z 。
4：输出项有四个，竖着切会输出左右三角形顶点数据，横着切会输出上下三角形顶点数据。

「Step.2.2」：生成体素格子「Span」
- 记录 x ， z 坐标对应的的编号 idx = x + z * Heightfield.width
- 更新 y 最低和最高值 Span.smin、 Span.smax
- 更新行走状态 Span.area （0：不可行走，63：可行走）
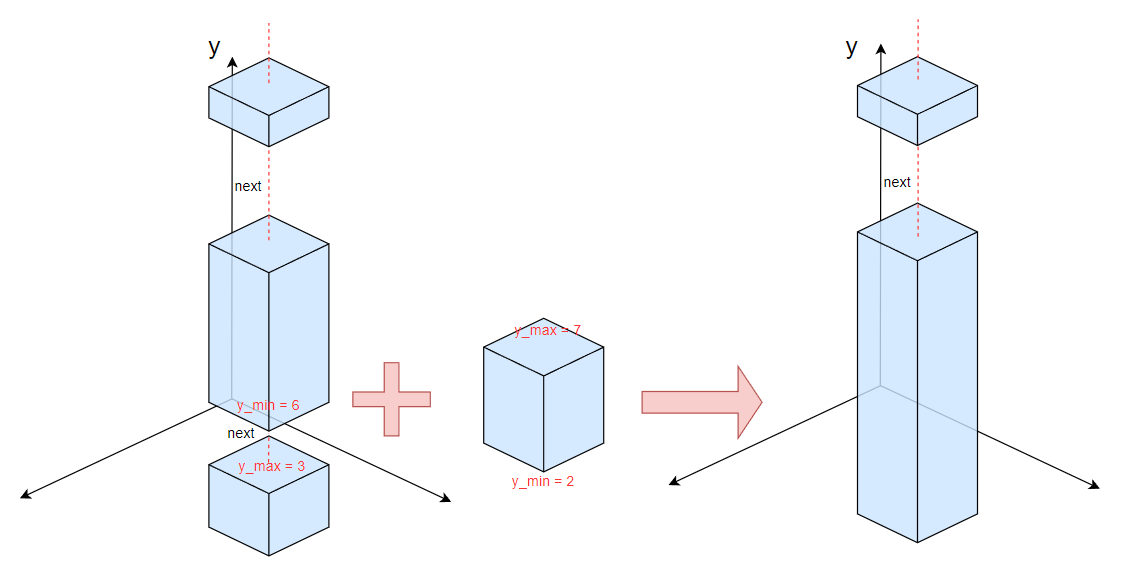
「Step.2.3」：「Span」合批
- 如果两个「Span」的 idx 相同，且 y 轴覆盖范围有重叠，且合并后「Span」的 Span.smin 和 Span.smax 的高度差不超过「MaxClimb」，则进行合并，并更新 Span.area、Span.smax、Span.smin

# Filter walkables surfaces

处理配置内的三个过滤项：

Low Hanging Obstacles：计算可以攀爬区域。
Ledge Spans：缩小突起区域的外轮廓。
Walkable Low Height Spans：剔除不可站立区域。

# Low Hanging Obstacles

如果「Span」本身不可达，但可通过其他「Span」攀爬到达，其也将视为可达区域，受配置项「MaxClimb」影响

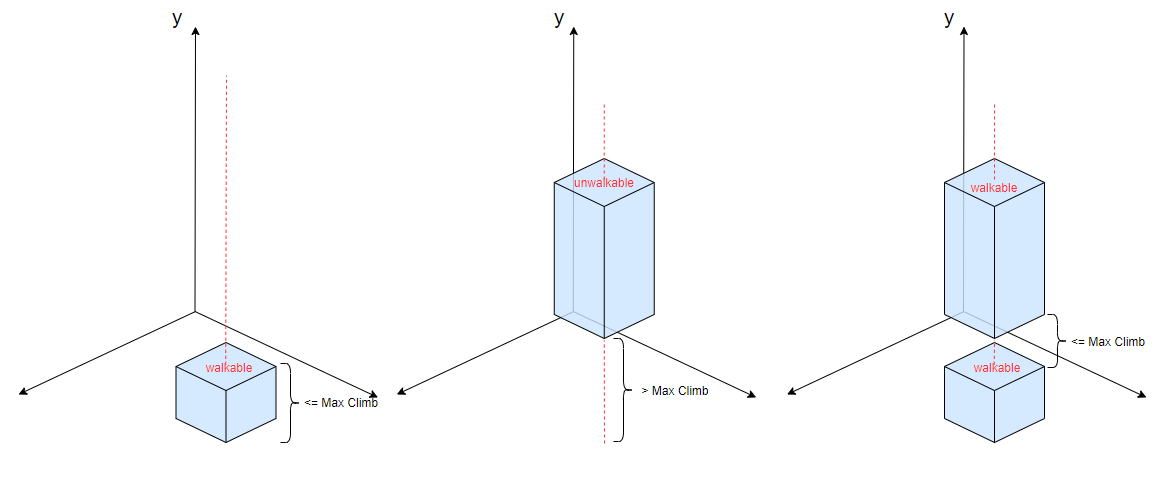
# Ledge Spans

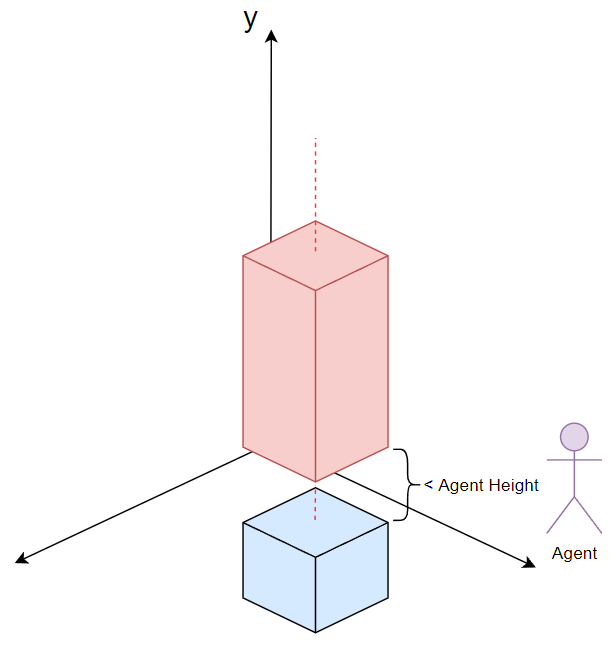
如果「Span」可站立（距离上表面高度大于「Agent Height」）且高于周围「Span」「MaxClimb」，那么视作不可达

表现上来说可以缩减突起部分的不可达区域

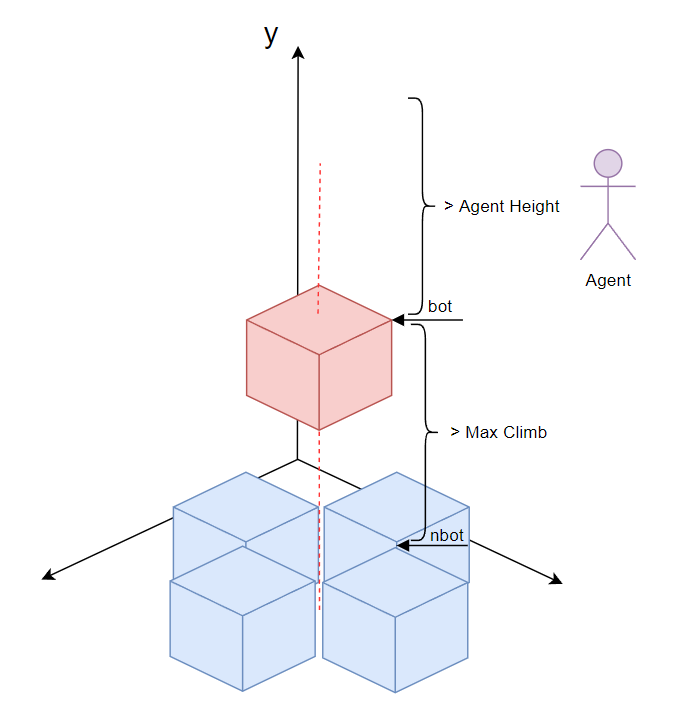
开启前：

开启后：

# Walkable Low Height Spans

剔除不可站立区域，受到配置项「Agent Height」影响。

如果同一列的「Span」间隙小于「Agent Height」，那么移动对象不能在其中站立，因此也表现为不可达

# Partition walkable surface to simple regions

找出所有的可达区域，并合并为「Region」

# BuildCompactHeightfield

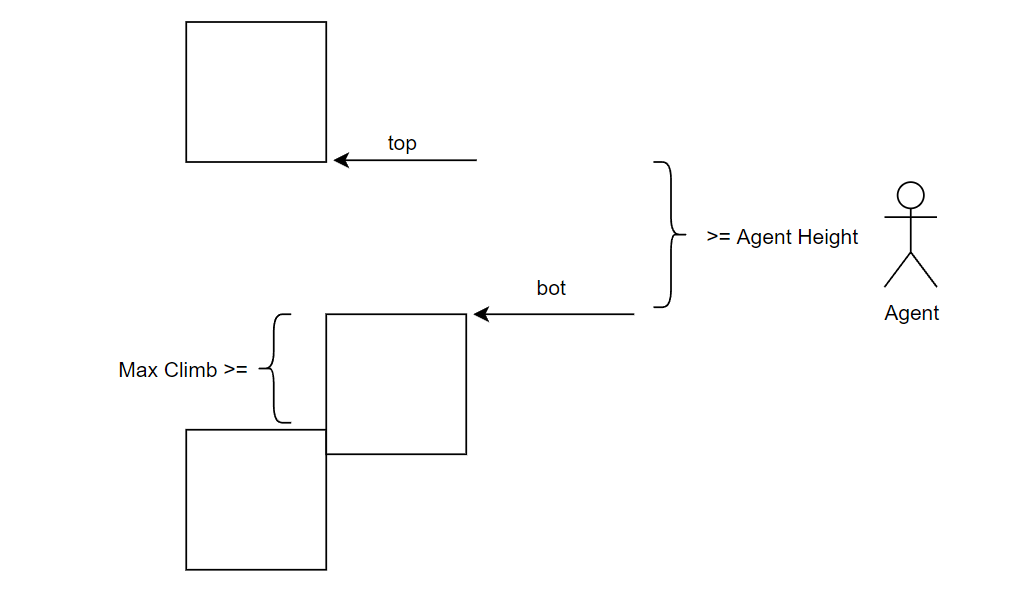
「Step.1」在可达区域构建「CompactSpan」，并记录连通情况

连通判定：和周围「CompactSpan」高度差不超过「MaxClimb」，两者最小高度差大于「Agent Height」

	// Check that the gap between the spans is walkable,
	// and that the climb height between the gaps is not too high.
	if ((top - bot) >= walkableHeight && rcAbs((int)ns.y - (int)s.y) <= walkableClimb)
	{
	// Mark direction as walkable.
	const int lidx = k - (int)nc.index;
	rcSetCon(s, dir, lidx);
	break;
	}

# ErodeWalkableArea

辐射遍历，计算场距

「Step.2」：根据「Agent Radius」辐射计算出可行走范围

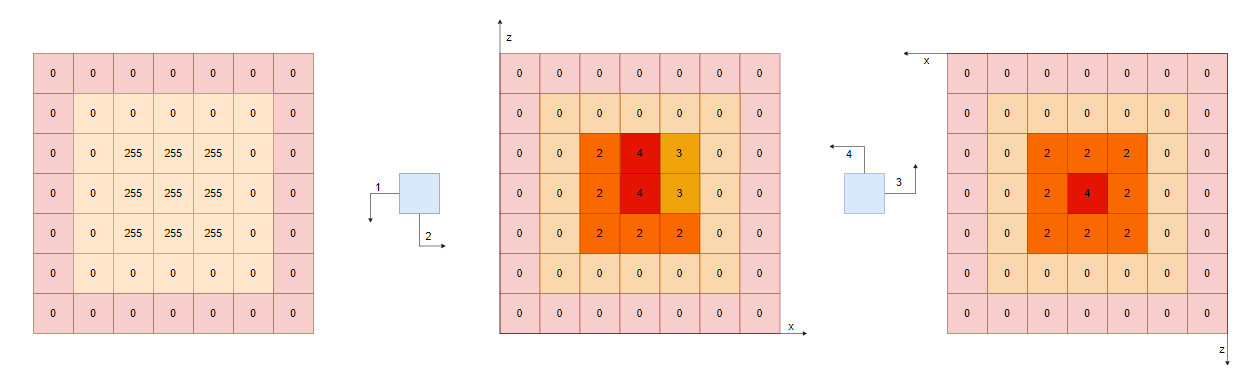
初始化场距：把边界处（邻居小于 4 ）的「CompactSpan」的「Distance」标记为 0 其他标记为 0ff

两轮 pass 用于更新场距，记录每个「CompactSpan」到边界的距离：

「Pass.1」：每个「CompactSpan」按照「左、左下」和「下、右下」的顺序遍历邻居，距离计算：

	//dist [i] 当前「span」的「distance」
	//dist [ai] 相邻「span」的「distance」
	// 横纵坐标距离 + 2.
	// 斜向坐标距离 + 3.
	nd = (unsigned char)rcMin((int)dist[ai]+2, 0xff);
	if (nd < dist[i])
	dist[i] = nd;

「Pass.2」：每个「CompactSpan」按照「右、右上」和「上、左上」的顺序遍历邻居

将「Distance」小于 2 *「Agent Radius」的「CompactSpan」标记为不可达。

# MarkConvexPolyArea

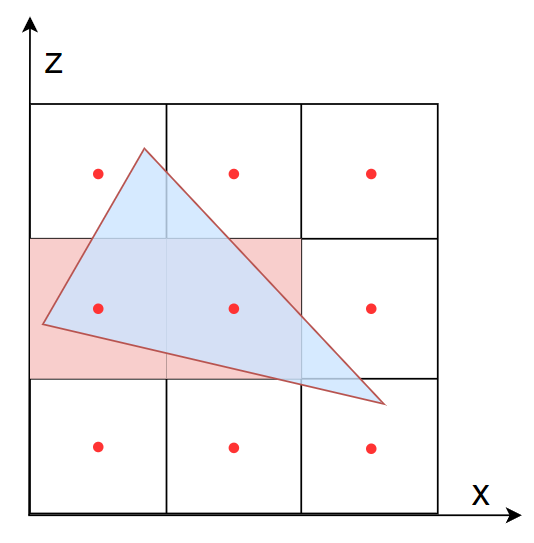
「Step.3」：标记「CompactSpan」的三角形归属及地形类型

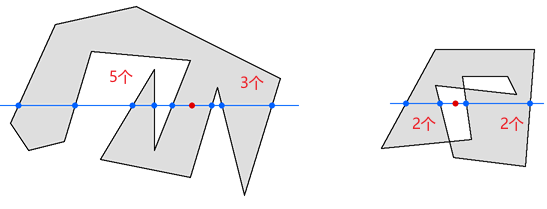
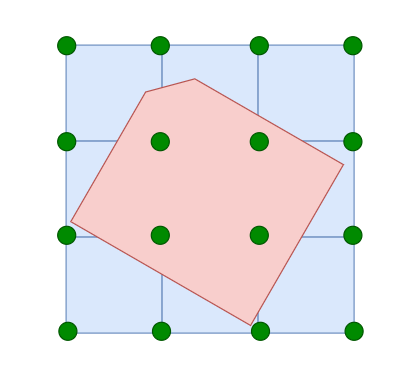
判定依据：「CompactSpan」xz-plane 平面的中点是否在三角形内
中点是否在多边形内的算法代码 —— 文章链接

	// 过「中点 p」沿着多边形的 x 轴切一刀，和多边形存在左右数个交点
	// 必须满足左右交点数量都是奇数的情况下，才表示「中点 p」在多边形内
	static int pointInPoly(int nvert, const float* verts, const float* p)
	{
	int i, j, c = 0;
	for (i = 0, j = nvert-1; i < nvert; j = i++)
	{
	const float* vi = &verts[i*3];
	const float* vj = &verts[j*3];
	if (((vi[2] > p[2]) != (vj[2] > p[2])) &&
	(p[0] < (vj[0]-vi[0]) * (p[2]-vi[2]) / (vj[2]-vi[2]) + vi[0]) )
	c = !c;
	}
	return c;
	}

标记「CompactSpan」的地形类型「AreaType」：
- SAMPLE_POLYAREA_GROUND：地面
- SAMPLE_POLYAREA_WATER：水
- SAMPLE_POLYAREA_ROAD：公路
- SAMPLE_POLYAREA_DOOR：门
- SAMPLE_POLYAREA_GRASS：草地（默认）
- SAMPLE_POLYAREA_JUMP：跳跃点

# Partition the heightfield⭐️

划分高度场。目前支持的三种高度场划分算法：

分层算法
单调分割算法
分水岭算法

# 分层算法

受到配置项「MinRegionSize」影响

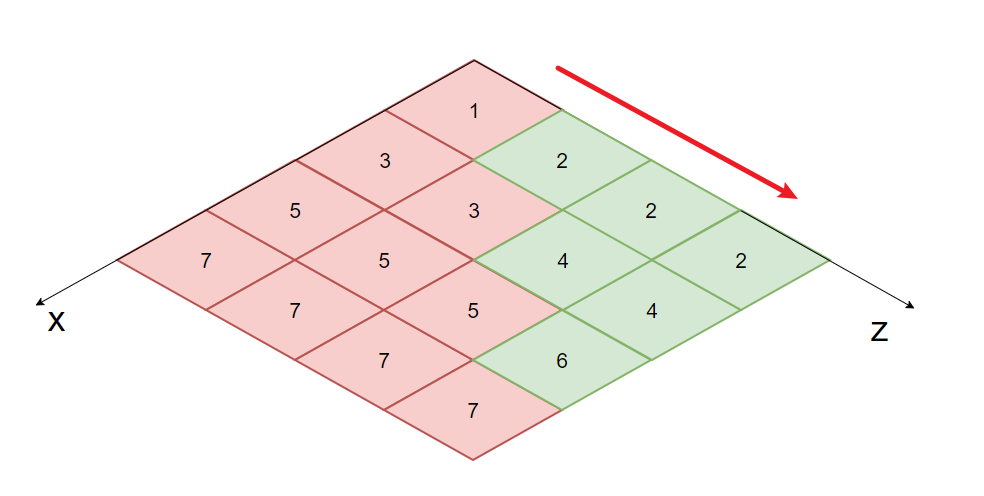
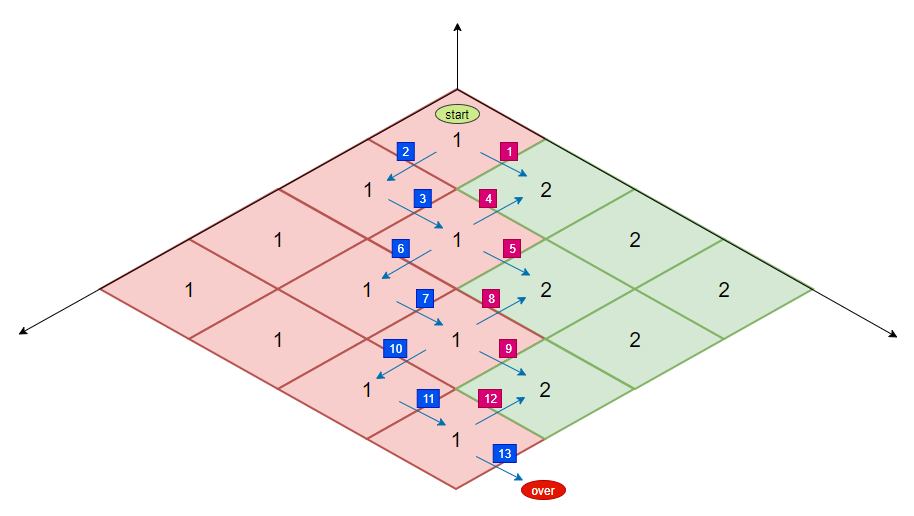
「Step.1」：标记所有「CompactSpan」的 region_id
- 先沿着 z 轴方向标记 region_id ，「AreaType」相同，下个「CompactSpan」继承上个 region_id
- 同 region_id 的「CompactSpan」视作同一「SweepSpan」
- 红绿分别表示不同「AreaType」
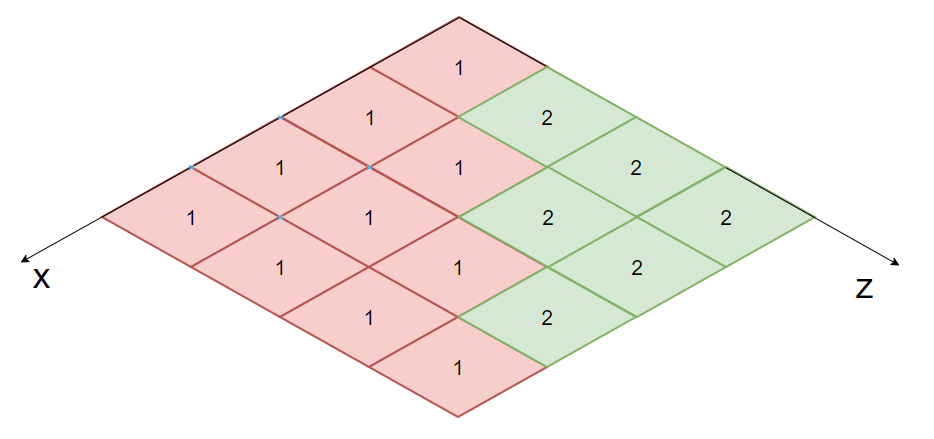
- 再先沿着 x 轴方向标记 region_id ，「AreaType」相同，下个「SweepSpan」继承上个 region_id

# MergeAndFilterLayerRegions

「Step.2」：更新「Region」之间的连接关系

更新 xz-plane 每个「CompactSpan」的四个方向的 connect ，并加入到「Region」

	// Update neighbours
	for (int dir = 0; dir < 4; ++dir)
	{
	if (rcGetCon(s, dir) != RC_NOT_CONNECTED)
	{
	const int ax = x + rcGetDirOffsetX(dir);
	const int ay = y + rcGetDirOffsetY(dir);
	const int ai = (int)chf.cells[ax+ay*w].index + rcGetCon(s, dir);
	const unsigned short rai = srcReg[ai];
	if (rai > 0 && rai < nreg && rai != ri)
	addUniqueConnection(reg, rai); // link
	if (rai & RC_BORDER_REG)
	reg.connectsToBorder = true;
	}
	}

再对同 y 轴上的「CompactSpan」两两更新 floor ，并加入到「Region」

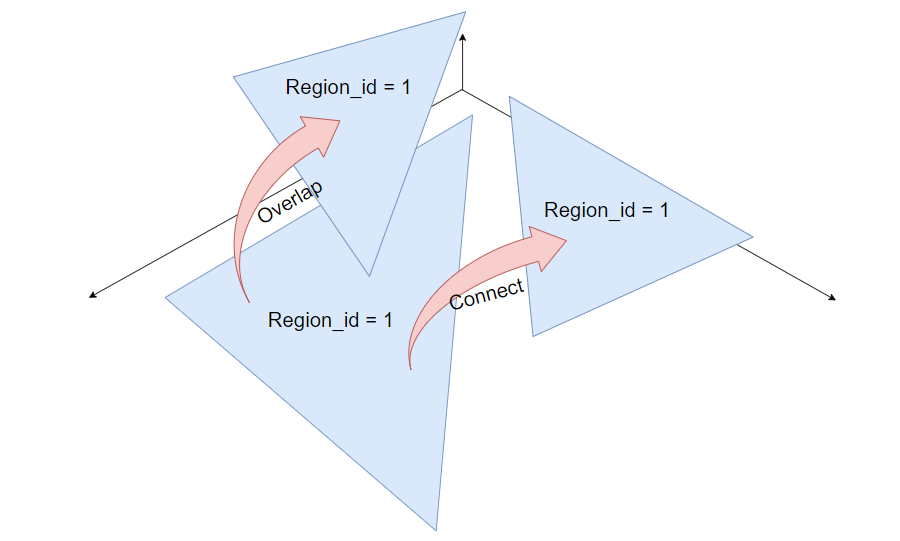
「Step.3」：DFS 遍历「Region」两两之间 connect 且无 overlap 的情况下，更新两边的 floor 集合
「Step.4」：计算通过 connect 合并后 spanCount 数量依旧不满足「MinRegionSize」的「Region」

	// Remove small regions
	for (int i = 0; i < nreg; ++i)
	{
	if (regions[i].spanCount > 0 && regions[i].spanCount < minRegionArea && !regions[i].connectsToBorder)
	{
	unsigned short reg = regions[i].id;
	for (int j = 0; j < nreg; ++j)
	if (regions[j].id == reg)
	regions[j].id = 0;
	}
	}

# 单调分割算法

受到配置项「MinRegionSize」和「MergedRegionSize」影响

「Step.1」和「分层算法的 Step.1」完全一致，用于划分「Region」

# MergeAndFilterRegions

「Step.2」：按照 y 轴从下往上更新「Region」之间两两的 floor 关系
「Step.3」：更新「Region」之间的 connect 关系 ——WalkContour

# WalkContour

坚固边缘：处在边界处或者「Region」分割线周围的「CompactSpan」，邻居数小于 4 或邻居 region_id 不同

边界区域查询：遍历位于「坚固边缘」的「CompactSpan」
- 如果邻居 region_id 不同，那么加入 Region.connections ，并顺时针旋转查询方向，继续查询
- 如果邻居非「坚固边缘」那么逆时针旋转方向，继续查询
最后对 Region.connections 去重

「Step.4」：剔除不满足条件的「Region」

剔除 spancount 小于「MinRegionSize」的「Region」
「Region」和周围 spancount 最少的「Region」合并，合并条件：
- 两者不存在 overlap 关系
- 两者都不是边界区域
- 其中一方数量 spancount 不超过「MergedRegionSize」

	static bool mergeRegions(rcRegion& rega, rcRegion& regb){
	// 1. rega.connections += regb.connections; set(rega.connections)
	// 2. rega.floors += regb.floors; set(rega.floors)
	// 3. rega.spanCount += regb.spanCount; regb.spanCount = 0;
	}

合并后，更新关联了「regb」引用为「rega」

# 分水岭算法

受到配置项「MinRegionSize」和「MergedRegionSize」影响

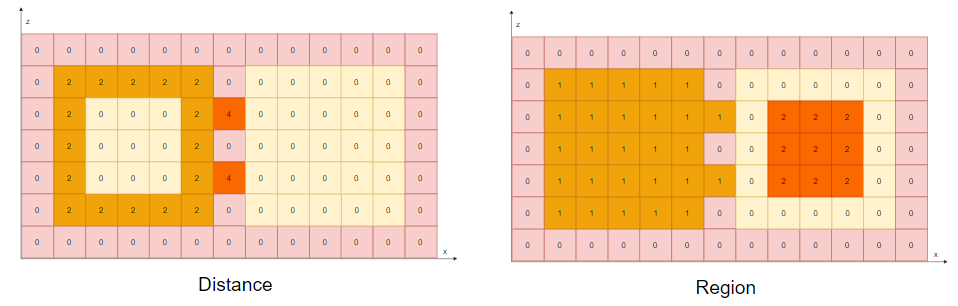
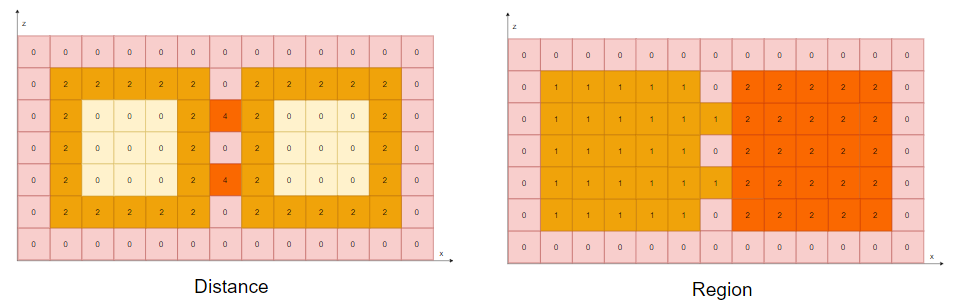
# CalculateDistanceField

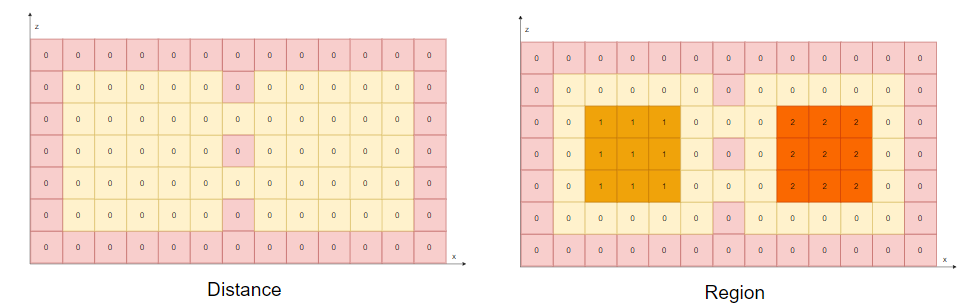
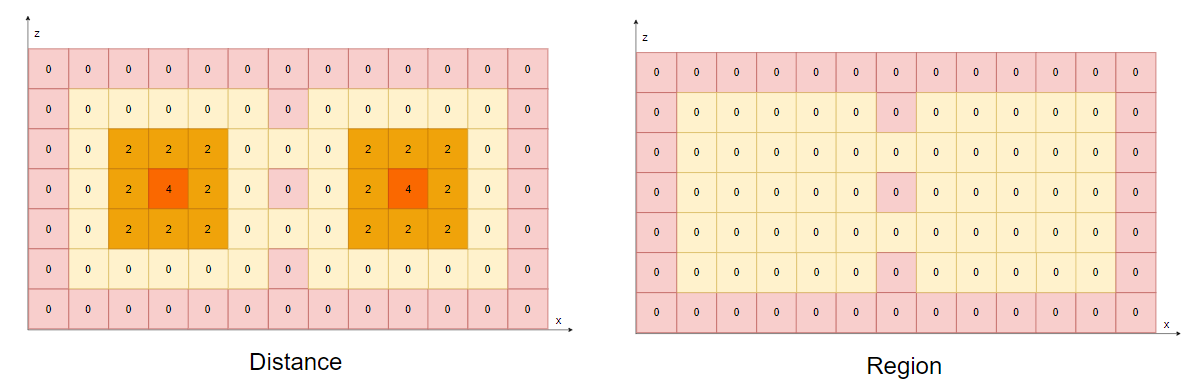
「Step.1」：计算场距，效果等价于 ErodeWalkableArea ，得到如下的距离场图：
- 左边记录了每个「CompactSpan」的场距
- 右边则是每个「CompactSpan」的 region_id
- 红色方框表示不可达区域

DistanceField

# BoxBlur

「Step.2」：对九宫格做一个模糊操作，使得场距过渡更加的圆滑

	// 伪代码
	// (sum (九宫格) + 5) / 9
	boxBlur(){
	span.distance = (short)sum(8个neighbor.distance) + 5 / 9;
	}

# BuildRegions

「Step.3」：根据分水岭算法划分「Region」
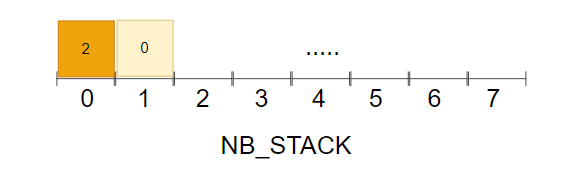
- 数据结构介绍：
  - nbstack ：长度为 8 ，元素是 256 个 LevelStackEntry 的栈
  - LevelStackEntry ：记录了每个「CompactSpan」的位置信息 [x,y,z]
- 从最大场距开始，这里假设是 4 ，向下做「漫灌」操作 sortCellsByLevel
  - 距离场每相差 2 个单位归为一层。每层数据被记录在 nbstack 的一个栈元素中
  - 这里对内存做了一定优化，每次先处理 8 层的「CompactSpan」
  - 以上图 DistanceField 为例，把场距是 2 和 0 的「CompactSpan」全部入栈
- 遍历 nbstack 的 8 个栈元素
  - 对每个栈做 expandRegions 来扩张「Region」
  - 遍历其中一个栈的全部「CompactSpan」
  - 如果「CompactSpan」已经有 region_id 则跳过
  - 如果「CompactSpan」没有 region_id ，其 region_id 同周围 4 个邻居中场距最小的
  - 重复执行 8 次（困惑中🤔）或中途所有的「CompactSpan」都标记了 region_id 则结束
    // 伪代码
    for neighbor_span in neighbor{
    if negihbor_span.distance is_min in neighbor{
    region_id = neighbor_span.region_id;
    distance = neighbor_span.distance + 2;
    }
    }
- 再对栈的每个「CompactSpan」做 floodRegion 来「淹没」更高的未被标记区域和第一次初始化区域。
  - 遍历其中一个栈的全部「CompactSpan」，并设置其 region_id 和 distance
  for span in nbstack[0~7]{
  span.region_id = regionId;
  span.distance = 0;
  }
  - DFS 周围 8 个邻居，如果邻居没有 region_id 并且大于自己的场距离（ 2 ），那么该邻居的 region_id 同自身。注：下图为遍历完 nbstack[0] 的结果。
  - 如果「CompactSpan」周围 8 个邻居有一个已经存在 region_id 了，并且和自己不同，则表示遇到了两个「Region」的边界 —— 如下图右侧 2 周围的一圈 0 。注：下图为遍历完 nbstack[1] 的结果。
  - 边界部分留到下一次处理，最终的边界会跟随「Distance」更小一方的 region_id ，最终结果：
「Step.4」：又做一遍 expandRegions （困惑中🤔）注释代码后的网格也挺正常，可能处理某些特殊情况
「Step.5」同「单调分割算法」的「mergeAndFilterRegions」

# 总结

三种分割算法的优劣描述：

分层算法：
- 「mergeAndFilterLayerRegions」先更新的 connect 再更新的 floor ，使得「Region」更加趋于扁平，对于平坦无高耸建筑等层级维度简单的地图较为友好。
- 「mergeAndFilterLayerRegions」全量遍历了「CompactSpan」，所以比起「单调分割算法」慢
单调分割算法：
- 「mergeAndFilterRegions」先更新的 floor 再更新的 connect ，使得「Region」更加趋于立体，对于复杂多层级的高耸建筑较为合适。
- 「mergeAndFilterRegions」对于「CompactSpan」遍历用了「walkContour」更加效率，所以比起「分层算法」快。
分水岭算法：
- 划分「Region」用的是「ErodeWalkableArea」，等于做了两遍「CompactSpan」遍历，但划分出来的效果相较于「单调分割算法」更加的均匀，分界线比较的适中。
- 虽然也使用了「mergeAndFilterRegions」，还是会比「分层算法」慢。

	// Partition the heightfield so that we can use simple algorithm later to triangulate the walkable areas.
	// There are 3 martitioning methods, each with some pros and cons:
	// 1) Watershed partitioning
	// - the classic Recast partitioning
	// - creates the nicest tessellation
	// - usually slowest
	// - partitions the heightfield into nice regions without holes or overlaps
	// - the are some corner cases where this method creates produces holes and overlaps
	// - holes may appear when a small obstacles is close to large open area (triangulation can handle this)
	// - overlaps may occur if you have narrow spiral corridors (i.e stairs), this make triangulation to fail
	// * generally the best choice if you precompute the nacmesh, use this if you have large open areas
	// 2) Monotone partioning
	// - fastest
	// - partitions the heightfield into regions without holes and overlaps (guaranteed)
	// - creates long thin polygons, which sometimes causes paths with detours
	// * use this if you want fast navmesh generation
	// 3) Layer partitoining
	// - quite fast
	// - partitions the heighfield into non-overlapping regions
	// - relies on the triangulation code to cope with holes (thus slower than monotone partitioning)
	// - produces better triangles than monotone partitioning
	// - does not have the corner cases of watershed partitioning
	// - can be slow and create a bit ugly tessellation (still better than monotone)
	// if you have large open areas with small obstacles (not a problem if you use tiles)
	// * good choice to use for tiled navmesh with medium and small sized tiles

# Trace and simplify region contours

计算「Region」的轮廓「Contour」，受到配置项「MaxEdgeError」和「MaxEdgeLength」影响

# BuildContours

「Step.1」：以「CompactSpan」为单位，记录和周围「Region」关系 —— flags
- 记录结构为 4 bit，每个 bit 表示一个方向， 0 表示同 region_id ， 1 表示不同。
  if (neighbor.region_id == cur.region_id)
  res |= (1 << dir); // dir 0~4
  cur_flag = res ^ 0xf;
「Step.2」：查找「Region」之间的边界，得到边界顶点轮廓
- 查询处在边界位置的「CompactSpan」，跳过以下三种情况：
  - == 0 ：周围没有连通 —— 孤岛
  - == 0xf ：周围都是同 region_id—— 内陆
  - 自己在分割线上或者没有 region_id
  if (flags[i] == 0 || flags[i] == 0xf){
  flags[i] = 0;
  continue;
  }
  if (!reg || (reg & RC_BORDER_REG))
  continue;
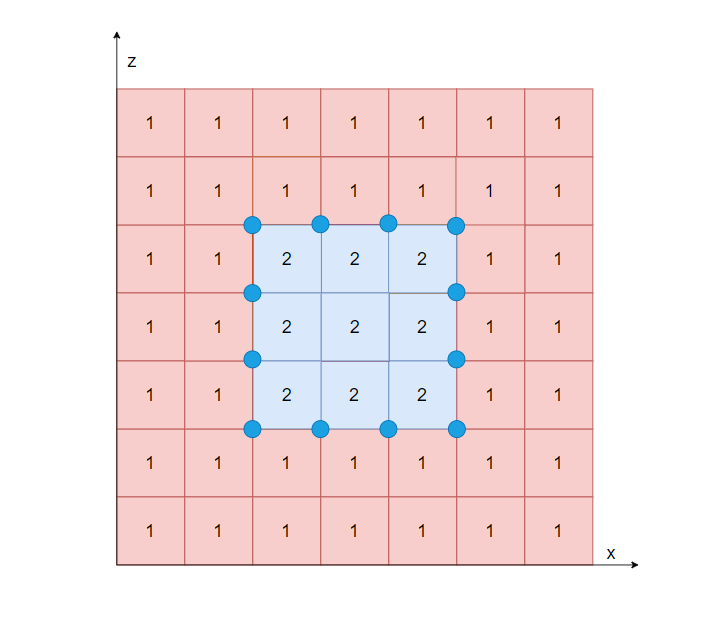
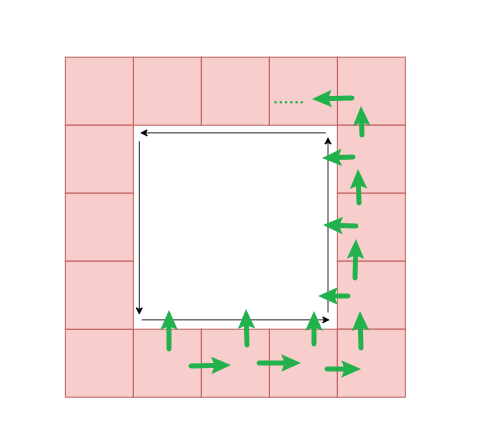
- 对当处在边界位置的「CompactSpan」执行一次 WalkContour 查询
  - 从一个边界方向开始查询，遇到边界后顺时针旋转 90° 继续查询，否则更新位置后逆时针旋转 90° 继续查询
  - 得到下图蓝色点组成的顶点轮廓
  - 注意这里获得的轮廓方向，这点很重要，轮廓的顺逆将决定多边形是凸还是凹
    - 「Region.1」的内圈轮廓是逆时针的，所以是一个凹多边形
  - 「Region.2」的外圈轮廓是顺时针的，所以是一个凸多边形

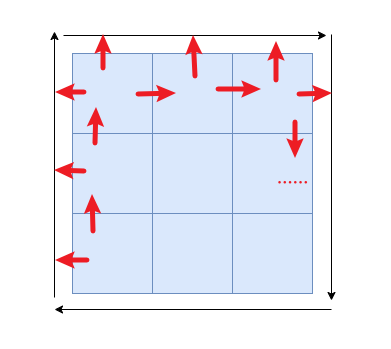
# GetCornerHeight

「Step.3」：获取区域的高度
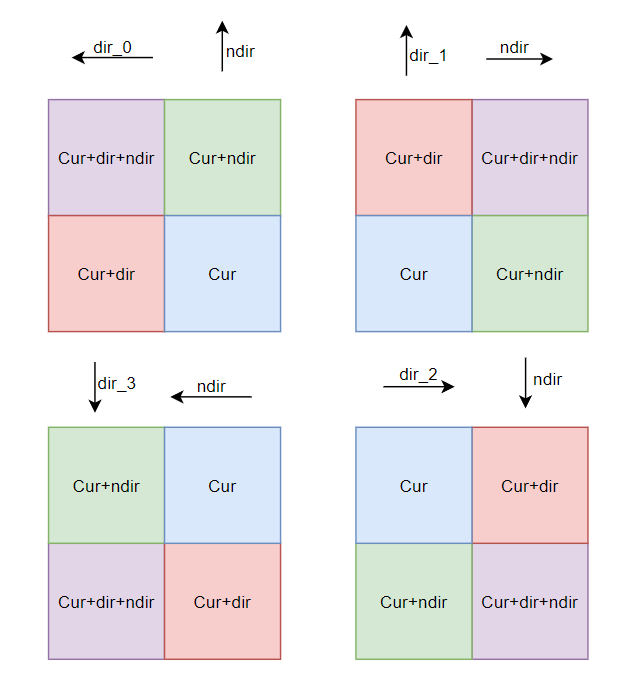
- 数据结构： 4 个 int 组成的数组， int 前 16 位表示「AreaType」后 16 位表示 region_id
  - [0] ：当前「CompactSpan」
  - [1] ：当前「CompactSpan」+ dir
  - [2] ：当前「CompactSpan」 + dir + next_dir or 当前「CompactSpan」 + next_dir + dir
  - [3] ：当前「CompactSpan」+ next_dir
- 如下是每种 dir 对应的 next_dir ：
  // dir next_dir
  // ← ↑
  // ↑ →
  // → ↓
  // ↓ ←
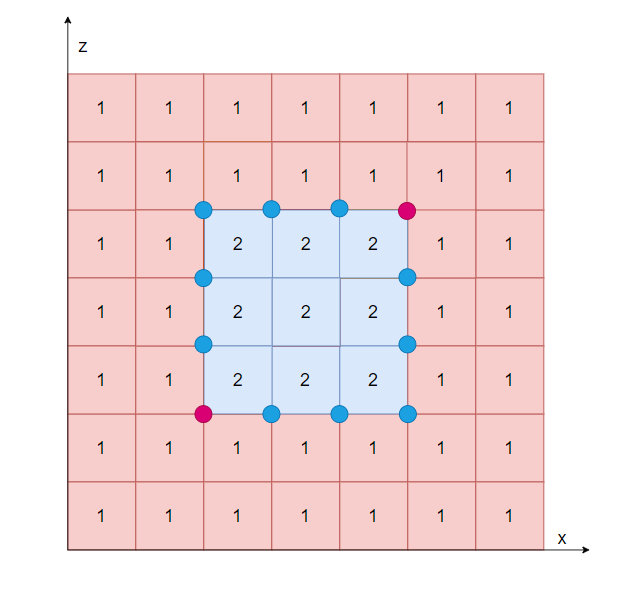
- 取四个方位 max(CompactSpan.y) 作为「区域高度」
- 遇边界跳过并打上 RC_BORDER_VERTEX 标记，边界判定规则：
  - 其中相邻两个「CompactSpan」都是边界，且 region_id 相同
  - 另外两个「CompactSpan」都不是边界
  - 另外两个「CompactSpan」的「AreaType」相同
  - 所有「CompactSpan」都有 region_id

以四个「CompactSpan」的右上方「CompactSpan」的左下角作为坐标点（四个「CompactSpan」的中心位置）并记录高度

	// rcIntArray points(256);
	switch(dir)
	{
	case 0: pz++; break;
	case 1: px++; pz++; break;
	case 2: px++; break;
	}
	points.push(px); // x
	points.push(py); // y
	points.push(pz); // z
	points.push(r); // negihbor region_id or AREA_BORDER or BORDER_VERTEX

# SimplifyContour

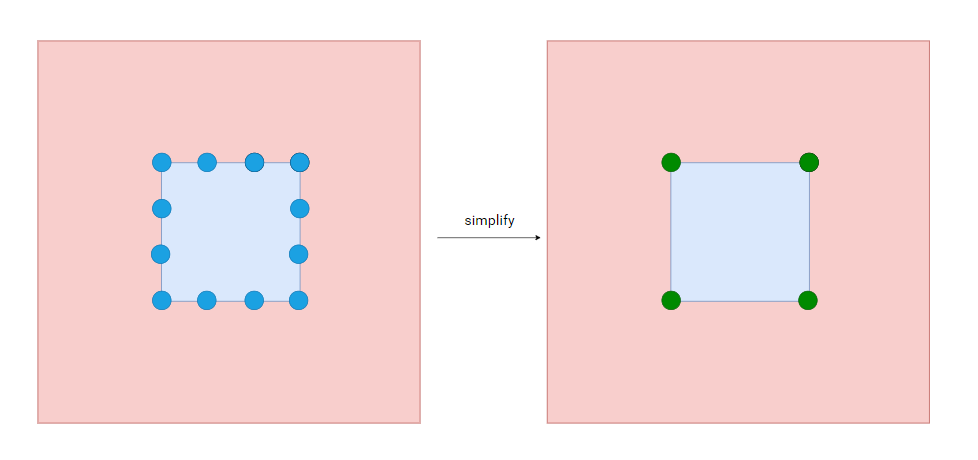
「Step.4」：对得到顶点数组做一个「simplify」。
- 简化顶点轮廓
  - 把顶点数组内左下角和右上角的点加入「simplify」
  - 每个点和后一个比较，如果两个点记录的 neighbor.region_id 或「AreaType」相同，则忽略
  - 结果如下：按理图中所有点的 neighbor.region_id 都相同，所以只记录了左下和右上点

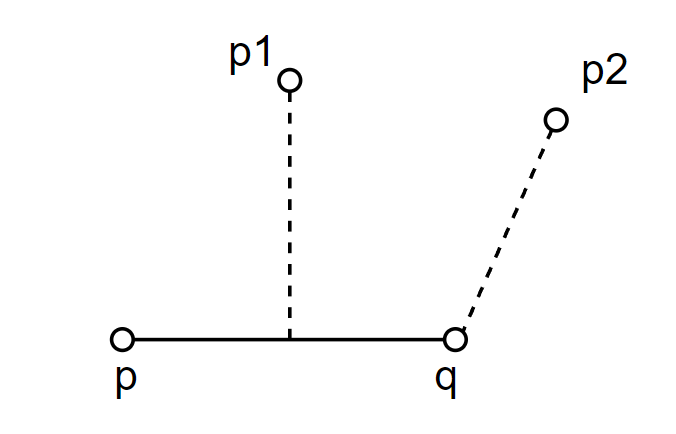
# DistancePtSeg

计算点到线段距离，如果点和线段没有垂线交点，那么按照点和线段两头的最小距离作为点到线段距离

	static float distancePtSeg(const int x, const int z,
	const int px, const int pz,
	const int qx, const int qz)
	{
	float pqx = (float)(qx - px);
	float pqz = (float)(qz - pz);
	float dx = (float)(x - px);
	float dz = (float)(z - pz);
	float d = pqxpqx + pqzpqz;
	float t = pqxdx + pqzdz;
	if (d > 0)
	t /= d;
	if (t < 0)
	t = 0;
	else if (t > 1)
	t = 1;

	dx = px + t*pqx - x;
	dz = pz + t*pqz - z;

	return dxdx + dzdz;
	}

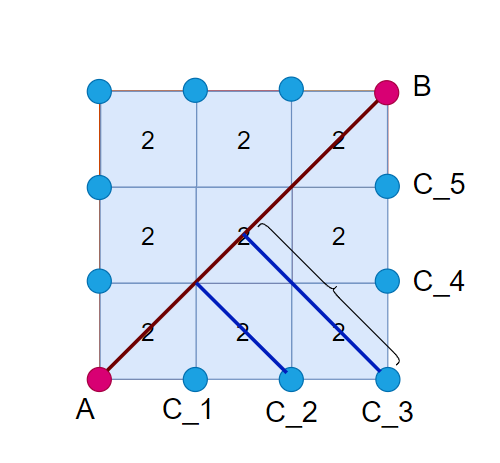
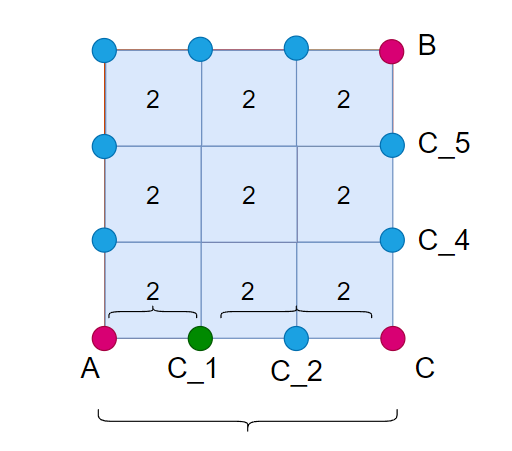
「Step.4.1」：把距离误差过大的点加回「simplify」
- 先按照顶点顺序进行排序
- 最大距离（ C_3 到 AB 线段）如果超过「MaxEdgeError」则把 C_3 也加入「simplify」数组
- 再次执行排序和计算距离，直到没有点到直线距离超过「MaxEdgeError」，则进行下一组顶点计算

「Step.4.2」：对「simplify」中两点所组成的过长边进行切分。

切分有两种，一种是切分贴墙的边，一种是切分「AreaType」的分界线，默认是切墙
相邻两个「simplify」中点的欧式距离超过「MaxEdgeLength」且中间有省略的点，则进行切分
- 切分规则直接查询两点中间编号的点作为中点，此处以 C_1 为中点切分
- 把 C_1 加入「simplify」并再次判断距离直到全部满足条件

「Step.4.3」：更新「simplify」中点的数据

继承自生的「边界标记」 BORDER_VERTEX 并继承下一个节点的「区域类型标记」 AREA_BORDER

	for (int i = 0; i < simplified.size()/4; ++i)
	{
	// The edge vertex flag is take from the current raw point,
	// and the neighbour region is take from the next raw point.
	const int ai = (simplified[i*4+3]+1) % pn;
	const int bi = simplified[i*4+3];
	simplified[i4+3] = (points[ai4+3] & (RC_CONTOUR_REG_MASK\|RC_AREA_BORDER)) \| (points[bi*4+3] & RC_BORDER_VERTEX);
	}

「Step.4.4」： removeDegenerateSegments ，剔除重叠顶点，同「Region」内 xz 坐标相同的点只保留一个
「Step.5」：记录「Region」简化后的顶点轮廓数组，最终结果如下：

Simplify

「Step.6」：通过多边形面积计算，判断凹凸，并计算凹多边形和凸多边形顶点直线距离

calcAreaOfPolygon2D 计算多边形 xz-plane 上的面积，这里用于辨别多边形是否是凸多边形，参考链接
也可以通过多边形是顺时针还是逆时针辨别，逆时针是凹多边形，顺时针是凸多边形

	static int calcAreaOfPolygon2D(const int* verts, const int nverts)
	{
	int area = 0;
	for (int i = 0, j = nverts-1; i < nverts; j=i++)
	{
	const int* vi = &verts[i*4];
	const int* vj = &verts[j*4];
	area += vi[0] * vj[2] - vj[0] * vi[2];
	}
	return (area+1) / 2; // > 0 is outlines else holes
	}

# MergeRegionHoles

「Step.7」：如果「Region」存在一个凸多边形和多个凹多边形，则进行合并 mergeRegionHoles ，参考链接
「Step.7.1」：根据左下角顶点大小对凹多边形进行排序 findLeftMostVertex

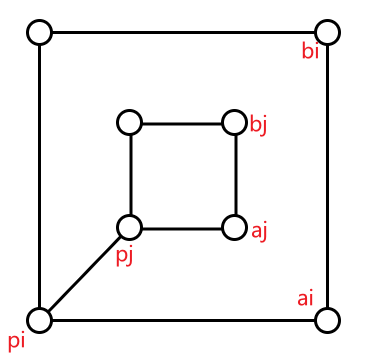
# InCone

	static bool inCone(int i, int n, const int* verts, const int* pj)
	{
	const int* pi = &verts[i * 4];
	const int* pi1 = &verts[next(i, n) * 4];
	const int* pin1 = &verts[prev(i, n) * 4];
	// If P[i] is a convex vertex [ i+1 left or on (i-1,i) ].
	if (leftOn(pin1, pi, pi1))
	return left(pi, pj, pin1) && left(pj, pi, pi1);
	// Assume (i-1,i,i+1) not collinear.
	// else P[i] is reflex.
	return !(leftOn(pi, pj, pi1) && leftOn(pj, pi, pin1));
	}

有两种满足 inCone 的情况：

【Con.1 right】： $\overrightarrow{pin1pi} \times \overrightarrow{pin1pi1} >= 0$ $p i n 1 p i \times p i n 1 p i 1 > = 0$ ： $\overrightarrow{pin1pi}$ $p i n 1 p i$ 顺时针旋转到 $\overrightarrow{pin1pi1}$ $p i n 1 p i 1$ 的夹角＞ 180°
- 点 pj 在区域①、③、④满足条件

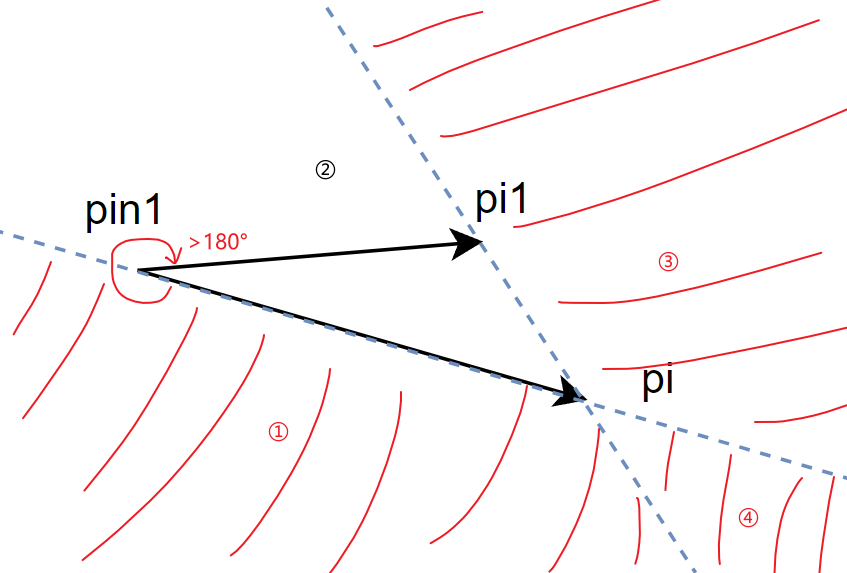
right

【Con.2 left】： $\overrightarrow{pin1pi} \times \overrightarrow{pin1pi1} <= 0$ $p i n 1 p i \times p i n 1 p i 1 < = 0$ ： $\overrightarrow{pin1pi}$ $p i n 1 p i$ 顺时针旋转到 $\overrightarrow{pin1pi1}$ $p i n 1 p i 1$ 的夹角 ≤ 180°
- 点 pj 在区域①满足条件

left

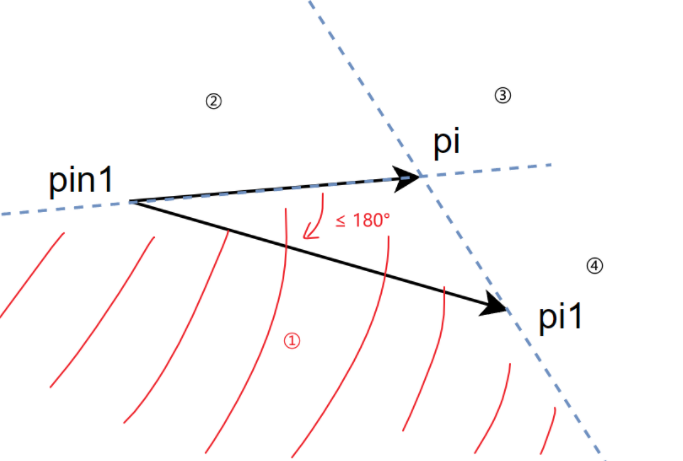
「Step.7.2」：计算凸多边形连续顶点 pi 、 pin1 、 pi1 与凹多边形的任意点 pj 「InCone」关系
- 计算满足「InCone」关系的顶点（凹多边形顶点在凸多边形内）的欧式距离 dist(pi, pj) 。
- 计算 $\overrightarrow{pipj}$ 和其他边是否相交 —— intersectSegCountour 参考链接
- 不存在相交情况则记录下该凸多边形顶点 pj ，并把该凹多边形合并到凸多边形内 MergeContours

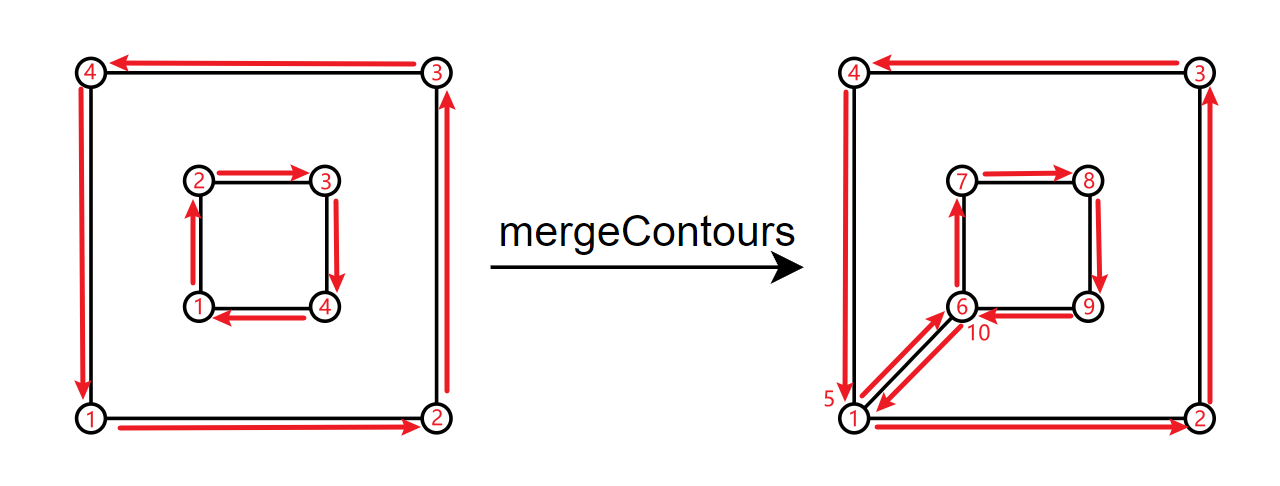
# MergeContours

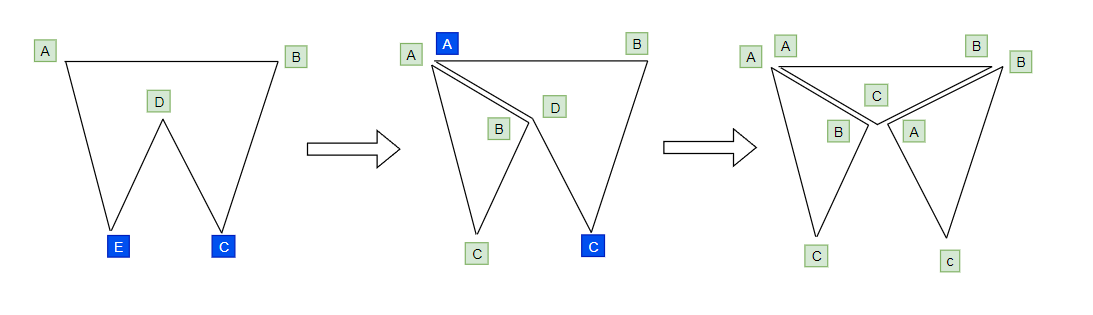
「Step.8」：合并凹多边形到凸多边形内
- 把所有凹多边形顶点拷贝到凸多边形顶点集内，顺带更新一下凸多边形顶点数量。
- new_outline_vec_count = old_hole_vec_count + old_outline_vec_count + 2

# Build polygons mesh from contours

通过「Region」的「Countour，构建「Mesh」，受到配置项「VertsPerPoly」影响

# BuildPolyMesh

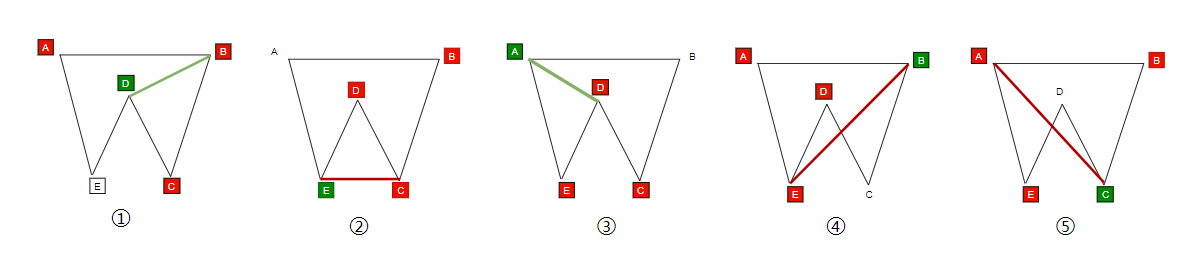
「Step.1」：遍历所有的「Countour」，找出所有的「切割点」 diagonal
- 取其中连续的四个顶点 pin1 、 pi 、 pi1 、 pj
- 如果 pin1 、 pi 、 pi1 和 pj 满足「InCone」关系，且不和自身的任意边相交
- 那么 $\overrightarrow{pipj}$ 一定是多边形内部的一个角平分线
- 下图中④、⑤都和自身边相交，②不满足「InCone」关系， $\triangle{BCD}$ 是凸多边形，E 在其外部
- 因此符合条件的只有①、③，对应的切割点是 C and E
「Step.2」：遍历所有满足条件的「切割点」，从相邻顶点距离最小的「切割点」开始切割，并对得到的两个多边形分别计算一次「切割点」 diagonal ，并继续切割，直到所有的「切割点」都被切掉
- 这里还有个小瑕疵：如果存在轮廓重叠的情况下， diagonal 将找不出重叠部分的「切割点」这时需要把重叠情况也考虑进来，用 diagonalLoose 再做一次「切割点」计算
「Step.3」：对顶点去重，并把三角形合并为多边形，合并条件如下：
- 合并后的多边形顶点数不超过「VertsPerPoly」
- 合并的两个多边形有一条公共边
- 合并后的多边形必须是凸多边形
「Step.4」：尝试移除带有边界标记 RC_BORDER_VERTEX 的顶点
- 判断移除条件 canRemoveVertex ：
  - 剔除顶点后的的多边形边长要超过 3
  - 剔除顶点关联的非共享边不超过 3
- 剔除顶点操作 removeVertex ：
  - 删除顶点数据和关联顶点的多边形
  - 重新按照边的首尾顺序拼接出新的多边形
  - 对新的多边形进行切割及合并，参考「Step.1」、「Step.2」、「Step.3」
  - 把新的多边形加入多边形集合
「Step.5」：计算多边形之间的相邻关系 buildMeshAdjacency

# Create detail mesh which allows to access approximate height on each polygon

根据采样步长和误差值把多边形细分成误差可接受范围内的三角形，受到配置项「SampleDistance」和「MaxSampleError」影响

# BuildPolyMeshDetail

「Step.1」：计算所有多边形的 xz 平面上包围盒，以及每个多边形自身的包围盒
「Step.2」：计算多边形包围盒的各个单位点的高度值 getHeightData ，高度取值用位于该点的同 region_id 的「CompactSpan」上表面坐标 CompactSpan.y
- 如果一个多边形包围盒内没有任何「CompactSpan」的 region_id 相同，说明该多边形和其他多边形存在重叠， region_id 用了其他多边形的，因此采用 seedArrayWithPolyCenter 采样法
  - 首先查询所有「CompactSpan」，计算和多边形表面最接近的「CompactSpan」，并且从该「CompactSpan」出发遍历相邻「CompactSpan」，直到靠近多边形中点的「CompactSpan」，并用该中心点的「CompactSpan」上表面作为多边形中心点高度

# BuildPolyDetail

「Step.3」：切割多边形的边
- 根据「SampleDistance」计算每条边的「切割点」，并计算「切割点」高度 getHeight
  - 获取「切割点」对应的「CompactSpan」上表面高度
  - 如果「切割点」本身没有对应的「CompactSpan」或者「CompactSpan」没有高度标记
  - 则取周围一圈 8 个「CompactSpan」误差最小的高度
  - 如果还是没有则再往外扩一圈，直到遇见一个有高度标记的「CompactSpan」作为该点高度
- 计算所有「切割点」到边的距离，如果距离超过「MaxSampleError」则可以进行切割
  - 把「切割点」加入边顶点集合，并对新的顶点再次两个为边长计算到「切割点」距离
  - 直到所有「切割点」都满足「MaxSampleError」或者切割定点数达到了 32 则终止。
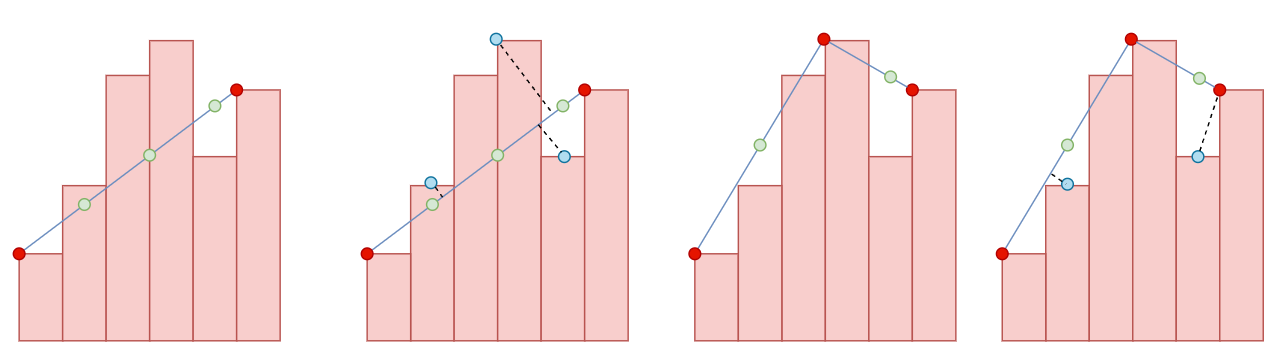
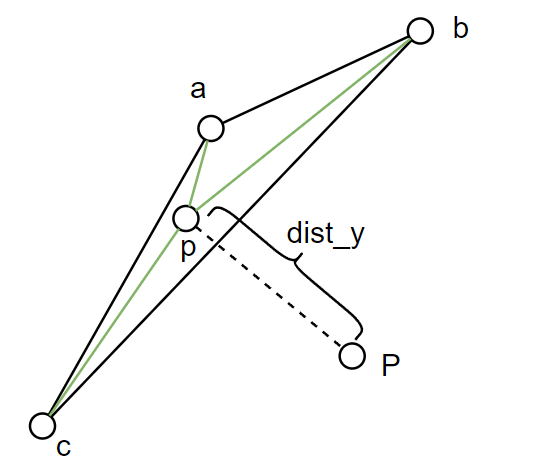
- 下图为单个边长切割流程
  - 红点：初始边长的顶点
  - 绿点：需要尝试切割的点
  - 蓝点：「切割点」的实际 y 坐标取值
  - 虚线：「切割点」到边长的距离
「Step.4」：通过获得的「切割点」，对多边形进行切割
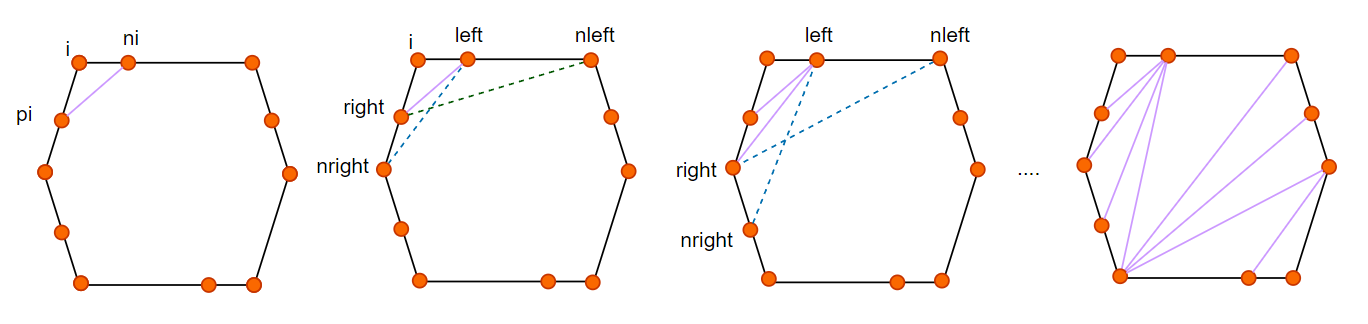
- 切割算法： triangulateHull
  - 取周长最小的三个连续顶点组成的三角形为起点开始切割
  - 对比左右两个点 nleft 、 nright 到 left 、 right 的距离
  - 其中最短的距离和作为下一个被切分出的三角形 $\triangle{p_{left}p_{nright}p_{right}}$
  - 更新 nright 为 right 继续切割，直到所有「切割点」都被切割完毕

「Step.5」：计算多边形的任意点到任意边线段的最短距离，仅计算分割前，不考虑 y 坐标，如果距离大于「SampleDistance」说明多边形较大，需要新增内部点来做进一步细化的切割

根据 xz-plane 按照「SampleDistance」为大小，网格化多边形
筛选掉靠近多边形边的网格点

对剩下的点进行 jittered 采样，随机取点周围 [-1, 1] 偏移范围内的一点作为采样点计算采样点到所有切割出的三角形的距离最大值 distToTriMesh

	inline float getJitterX(const int i)
	{
	return (((i * 0x8da6b343) & 0xffff) / 65535.0f * 2.0f) - 1.0f;
	}

	inline float getJitterY(const int i)
	{
	return (((i * 0xd8163841) & 0xffff) / 65535.0f * 2.0f) - 1.0f;
	}

计算采样点投影到三角形平面上的重心坐标 u,v ，重心坐标介绍
把中心坐标和采样点坐标的 y 轴差值作为采样点到三角形平面的距离
如果重心坐标落在三角形外，则距离为 -1
如果距离最大的点超过了「MaxSampleError」，那边把该点新增到多边形

# DelaunayHull

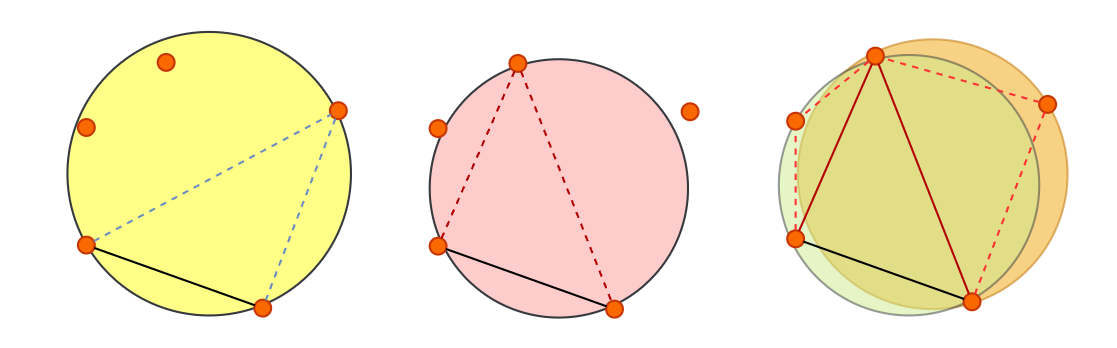
「Step.6」重新建立切分后的三角形布局
- 处理所有的顶点，根据相邻点建立连线，计算出线段和任意点组成的外接圆 CircumCircle，如果外接圆内不包含其它点，将组成该外接圆的三个点作为三角形的三个顶点，否则取连线和外接圆内的点生成更小的外接圆
- 把所有组成三角形的边记录下来，并记录边两侧的三角形编号 completeFacet

# CircumCircle

构建三角形的外接圆，以 p1 为原点，计算两条边中垂线的交点，返回圆心和半径。

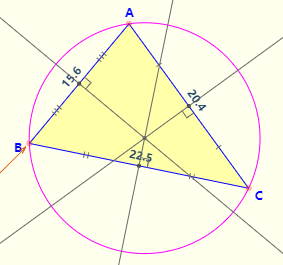
	static bool circumCircle(const float* p1, const float* p2, const float* p3,
	float* c, float& r)
	{
	static const float EPS = 1e-6f;
	// Calculate the circle relative to p1, to avoid some precision issues.
	const float v1[3] = {0,0,0};
	float v2[3], v3[3];
	rcVsub(v2, p2,p1);
	rcVsub(v3, p3,p1);

	const float cp = vcross2(v1, v2, v3);
	if (fabsf(cp) > EPS)
	{
	const float v1Sq = vdot2(v1,v1);
	const float v2Sq = vdot2(v2,v2);
	const float v3Sq = vdot2(v3,v3);
	c[0] = (v1Sq(v2[2]-v3[2]) + v2Sq(v3[2]-v1[2]) + v3Sq(v1[2]-v2[2])) / (2cp);
	c[1] = 0;
	c[2] = (v1Sq(v3[0]-v2[0]) + v2Sq(v1[0]-v3[0]) + v3Sq(v2[0]-v1[0])) / (2cp);
	r = vdist2(c, v1);
	rcVadd(c, c, p1);
	return true;
	}

	rcVcopy(c, p1);
	r = 0;
	return false;
	}

# Create Detour data from Recast poly mesh

# CreateNavMeshData

把之前得到的数据调整一下数据结构进行存储

「Step.1」Store header
「Step.2」Store vertices
「Step.3」Store polygons
「Step.4」Store detail meshes and vertices

# CreateBVTree

构建 BVTree

「Step.5」Store and create BVtree
- 按照某个坐标轴进行二分划分空间，计算两边的 AABB 和「Poly」

# InitNavMesh

「Step.6」初始化 navMesh，构建「Tile」，由于用的是「SoloMesh」方式，tile 只有 1 个，没啥操作

# InitNavQuery

「Step.7」初始化 navQuery，处理一下查询结构是否内存足够，不够的话 resize 一下，也没啥操作

	// 伪代码
	for neighbor_span in neighbor{
	if negihbor_span.distance is_min in neighbor{
	region_id = neighbor_span.region_id;
	distance = neighbor_span.distance + 2;
	}
	}

	for span in nbstack[0~7]{
	span.region_id = regionId;
	span.distance = 0;
	}

	if (neighbor.region_id == cur.region_id)
	res \|= (1 << dir); // dir 0~4
	cur_flag = res ^ 0xf;

	if (flags[i] == 0 \|\| flags[i] == 0xf){
	flags[i] = 0;
	continue;
	}

	if (!reg \|\| (reg & RC_BORDER_REG))
	continue;

	// dir next_dir
	// ← ↑
	// ↑ →
	// → ↓
	// ↓ ←