# PhysX——Transform 篇

用于描述 PhysX 系统下 Transform 操作的类，其提供了两个数据：

• PxQuat q：用于描述旋转的四元数 q
• PxVec3 p：用于描述平移的向量 p

# PxVec3

一个三维向量，用于表示一个物体从 A 点移动到 B 点所需的方向和距离

# PxQuat

四元数，用于描述三维空间下角度变化的数据结构，说到四元素，这里就不得不提到「旋转矩阵」和「欧拉角」，三者均用于表示空间层面的旋转。

• 四元数：由四个数字组成
• 旋转矩阵：由 3X3 的矩阵表示
• 欧拉角：由三个数字组成

在对四元数进行展开之前，先简单来聊聊「旋转矩阵」和「欧拉角」：

「旋转矩阵」在旋转方面的应用可以参考 Transform 文章，其中的一些证明就不再赘述，旋转矩阵的缺点就是需要用 9 个数表示，并且旋转计算效率较低，而且会产生矩阵蠕变（由于浮点数精度丢失导致的误差累积），在多次变换后使得矩阵本身不合法（非正交），需要通过正交化进行修正，但正交化性能消耗较高。不过「旋转矩阵」理解上相对较为简单，且 GPU 被设计成更适合进行矩阵运算，因此也被广泛应用在图形渲染领域。

「欧拉角」则通过 链式旋转 的方式，来实现到指定方向的旋转。这种旋转必须明确定义旋转的先后关系。例如 z>x>y。链式旋转一次操作等同于进行了三次不同坐标轴的旋转，理解上较为直观，但也引入了一个严重的问题：万向节死锁。其本质是由于链式旋转过程中基坐标变化，导致其中两个旋转轴发生重叠，丢失了其中一个维度的旋转能力。常见的解决办法：例如 Unity 下的摄像机通常通过限制旋转轴范围的方式来避免该问题。

接下来我们再来聊聊「四元数」：

「四元数」四元数的意义其实更在于数学层面，其思想来源于 罗德里格斯旋转公式 (Rodrigues’ Rotation Formula)，为了后续理解，简单介绍一下该旋转公式：

假定要把一个三维向量 $v$，围绕一个旋转轴 $u$，旋转 $\theta$ 角度。那么势必就可以把向量 $v$ 投影到轴 $u$ 及垂直于轴的平面上。

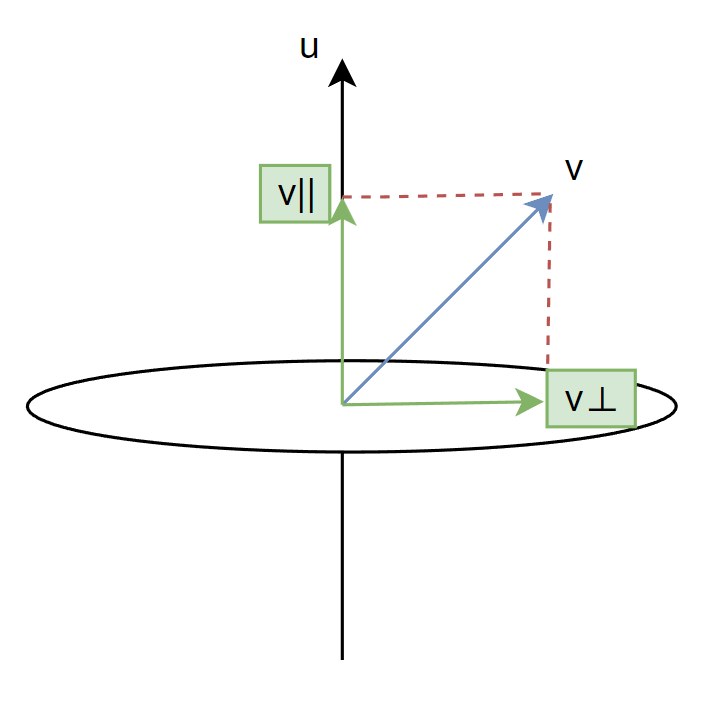
因此整个旋转也可以视为对 $v_\parallel$ 和 $v_\perp$ 绕 $v$ 轴进行旋转。然后根据三角函数和一些几何运算，就可以推导出一个普适的三维旋转公式：

介绍完旋转公式，接下来再来看看四元数的定义，四元数本身由三个虚部 + 一个实部组成：${\displaystyle a+b\ \mathbf {i} +c\ \mathbf {j} +d\ \mathbf {k} }$

这里再引入一个四元数的计算「Graßmann 积」，假定对两个四元数进行求积：

这里再对照虚部的计算规则 $i^2 = j^2 = k^2 = ijk = -1$，对 $q_1q_2$ 进行化简：

假设 $v=[b,c,d]^T, \quad u=[f,g,h]^T$，就可以推导出「Graßmann 积」的如下性质：

$$v \cdot u = bf + cg + dh \\ v \times u = [ch -dg,df - bh,bg - cf] \\ \text{再带入上面的q1q2公式:}\\ q_1q_2 = [ae - v \cdot u, au + ev + v \times u] \\ \text{对于 a，e 都为 0 的纯四元数又可以进一步简化：} \\ q_1q_2 = [-v \cdot u, v \times u]$$

再把上面推导出的「罗德里格斯旋转公式」进行套用：

到此，四元数旋转就推导完成了。除此以外，四元数还具备两个特殊的性质：「旋转叠加」和「旋转插值」。

# 旋转叠加

本质上就是对两次旋转进行合并，得到一个新的旋转结果，例如进行一个 $p_1$ 旋转后再进行 $p_2$ 旋转，四元数的表示： $p_2p_1vp_1^*p_2^*$

上述公式可以进一步化简：$p_2p_1v(p_2p_1)^*$，因此只需要计算一次 $p_2p_1$ 的结果即可，四元数乘法上面也已经介绍 $p_1p_2 = [ae - v \cdot u, au + ev + v \times u]$

# 旋转插值

假设旋转 p 是围绕某个轴旋转 1°，那根据「旋转叠加」，旋转 360° 可以写作 $p^{360} v {p^*}^{360}$。这里再根据上面的指数公式：

$$p = [cos(\frac{\theta}{2}), sin(\frac{\theta}{2})u] \text{，令：}q = p^2, \quad q = [cos(\theta), sin(\theta)u]$$

进行一般化和幂运算的求证（不在此证明），可以得到一个指数和 θ 角的关系：

$$p^n = [cos(n\frac{\theta}{2}), sin(n\frac{\theta}{2})u]$$

回过头来再看看的旋转，如果需要在 0~360° 之间进行插值，实际上就对于 p 中的 θ，在 0~360 进行插值。

把该规则一般化，变成可以在任意两个旋转 $p_0,p_1$ 内做插值，并且插值范围统一在 [0~1] 区间。

这里假设从 $p_0$ 旋转到 $p_1$ 的旋转为 $p\prime$ 那么就需要一个有关 ${p\prime}^t$ 的公式，在 ${p\prime}^0$ 的时候是 $p_0$，在 ${p\prime}^1$ 的时候是 $p_1$：

$${p\prime}^tp_0 = p_1 \text{，当前 t = 0 时结果为 p0，当 t = 1 时结果为 p1} \\ \text{因此：}p\prime p_0 = p_1 \\ p\prime = p_1p_0^* \\$$

计算求得插值的一般形式 $slerp(p_0, p_1, t) = {(p_1p_0^*)}^tp_0, t∈[0,1]$

# PxQuat 相关接口说明

前面简要介绍了有关四元数的计算过程，这里针对以上内容，结合实际代码来探讨一下 PhysX 内有关四元数的实现：

# 四元数的构造

根据之前的定义，四元数可以用来描述围绕某个单位轴旋转 θ 角旋转的操作 p：$[cos(\frac{θ}{2}), sin(\frac{θ}{2})i, sin(\frac{θ}{2})j, sin(\frac{θ}{2})k]$

对应到代码上来说 w 表示实部，x、y、z 表示 i、j、k：

PX_CUDA_CALLABLE PX_INLINE PxQuat(float angleRadians, const PxVec3& unitAxis)

{

    PX_ASSERT(PxAbs(1.0f - unitAxis.magnitude()) < 1e-3f);

    const float a = angleRadians * 0.5f;

    const float s = PxSin(a);

    w = PxCos(a); 		// cos(θ/2)

    x = unitAxis.x * s;	// sin{θ/2)i

    y = unitAxis.y * s;	// sin(θ/2)j

    z = unitAxis.z * s;	// sin(θ/2)k

}

# 四元数的加减法

这个比较简单，就是对应的实部和实部相加减，虚部和虚部相加减：

PX_CUDA_CALLABLE PX_FORCE_INLINE PxQuat& operator+=(const PxQuat& q)

{

    x += q.x;

    y += q.y;

    z += q.z;

    w += q.w;

    return *this;

}

PX_CUDA_CALLABLE PX_FORCE_INLINE PxQuat& operator-=(const PxQuat& q)

{

    x -= q.x;

    y -= q.y;

    z -= q.z;

    w -= q.w;

    return *this;

}

# 四元数的乘法

这个之前也介绍过了：

PX_CUDA_CALLABLE PX_INLINE PxQuat operator*(const PxQuat& q) const

{

    return PxQuat(w * q.x + q.w * x + y * q.z - q.y * z,  // w1x2 + w2x1 + y1z2 - z1y2

                  w * q.y + q.w * y + z * q.x - q.z * x,  // w1y2 + y1w2 + z1x2 - z2x1

                  w * q.z + q.w * z + x * q.y - q.x * y,  // w1z2 + w2z1 + x1y2 - x2y1

                  w * q.w - x * q.x - y * q.y - z * q.z); // w1w2 - x1x2 -y1y2 - z1z2

}

# 四元数的点乘

四元数的点乘意义在于假设四元数是四维空间中的向量，点乘用于求解两个四维向量夹角，计算方式其实和三维向量类似：

PX_CUDA_CALLABLE PX_FORCE_INLINE float dot(const PxQuat& v) const

{

	return x * v.x + y * v.y + z * v.z + w * v.w;

}

# 四元数的旋转

四元数的旋转和逆旋转表示相对抽象一些，但核心思想都是通过将四元数转成旋转矩阵，在进行矩阵变化，这里再计算上面用工程思想做了一定的简化操作。

这里简单对四元数进行矩阵展开，结果如下：

/**

rotates passed vec by this (assumed unitary)

*/

PX_CUDA_CALLABLE PX_FORCE_INLINE const PxVec3 rotate(const PxVec3& v) const

{

    const float vx = 2.0f * v.x; // 2x

    const float vy = 2.0f * v.y; // 2y

    const float vz = 2.0f * v.z; // 2z

    const float w2 = w * w - 0.5f; // a^2 - 0.5

    const float dot2 = (x * vx + y * vy + z * vz); // 2bx + 2cy + 2dz

    return PxVec3((vx * w2 + (y * vz - z * vy) * w + x * dot2),  // 2x(a^2 - 0.5) + (2cz - 2dy)a + b(2bx + 2cy + 2dz)

                  (vy * w2 + (z * vx - x * vz) * w + y * dot2),  // 2y(a^2 - 0.5) + (2dx - 2bz)a + c(2bx + 2cy + 2dz)

                  (vz * w2 + (x * vy - y * vx) * w + z * dot2)); //	2z(a^2 - 0.5) + (2by - 2cx)a + d(2bx + 2cy + 2dz)

}

/**

inverse rotates passed vec by this (assumed unitary)

*/

PX_CUDA_CALLABLE PX_FORCE_INLINE const PxVec3 rotateInv(const PxVec3& v) const

{

    const float vx = 2.0f * v.x;

    const float vy = 2.0f * v.y;

    const float vz = 2.0f * v.z;

    const float w2 = w * w - 0.5f;

    const float dot2 = (x * vx + y * vy + z * vz);

    return PxVec3((vx * w2 - (y * vz - z * vy) * w + x * dot2),

                  (vy * w2 - (z * vx - x * vz) * w + y * dot2),

                  (vz * w2 - (x * vy - y * vx) * w + z * dot2));

}

另外矩阵逆旋转 rotateInv ，表示旋转操作的反向，实际上可以视作旋转矩阵的虚部取反，即：$p = [a, -bi, -cj, -dk]$ 再带入旋转矩阵公式的结果；如果你对此足够有兴趣，不妨自己试试，应该和上面给出的实现相吻合。

# 四元素的叉乘

三维向量叉乘的意义在于，计算垂直于两个三维向量组成的平面的三维向量，一般用于已知两个互相垂直的坐标轴，求另一个坐标轴，来建立坐标系。

但对于四维空间这个计算实际上没有任何意义。即使需要构建四维坐标系，也需要已知三个互相垂直的四维向量，求另一个。因此，两个四元数的叉乘未被定义。

# PxTransform 接口说明

部分对子成员接口的封装这里就不再赘述，主要介绍几个比较重要的接口：

# Transform——vec3

坐标的旋转和平移实际上是两个变换，在 transform 接口中，两者有一个明确的优先级：先旋转再平移。

这里也比较好理解，如果把平移视作坐标加减，旋转视作坐标乘除。

一般情况下更倾向于先做乘除再做加减，这样能更好的调整位置。如果先做加减再做乘除，那么加减的值就不得不考虑乘除带来的影响。

PX_CUDA_CALLABLE PX_FORCE_INLINE PxVec3 transform(const PxVec3& input) const

{

    PX_ASSERT(isFinite());

    return q.rotate(input) + p;

}

# Transform——Transform

两个 transform 的叠加也是一个比较有意思的问题：这里以 src 作为基变换，在此基础上叠加自身的平移和旋转变换

• 旋转：上面讲到，关于旋转的叠加，实际上就是两个四元数的乘积，因此非常简单。

• 平移：对于平移，由于会受到旋转的影响，因此这里的平移叠加还考虑了基变换的旋转，用公式解释的话类似下面这种：

$$src_{transform}(input) = src.q.rotate(input) + src.p \\ cur_{transform}(src_{transform}(input)) = q.rotate(src.q.rotate(input) + src.p) + p \\ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad= q.rotate(src.p) + p + q.rotate(src.q.rotate(input)) \\ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad= q.rotate(src.p) + p + (q * src.q).rotate(input)$$

//! Transform transform to parent (returns compound transform: first src, then *this)

PX_CUDA_CALLABLE PX_FORCE_INLINE PxTransform transform(const PxTransform& src) const

{

    PX_ASSERT(src.isSane());

    PX_ASSERT(isSane());

    // src = [srct, srcr] -> [r*srct + t, r*srcr]

    return PxTransform(q.rotate(src.p) + p, q * src.q);

}

# Transform——Plane

这个也很有意思，PxPlane 在几何上的本意是平面，之所以放在 PxTransform 里面，是因为 PxPlane 本身的表示方式比较特殊。

PxPlane 通过一个垂直于平面的法向量 n 和一个距离原点的距离 d 来表示，实际上就是一个过原点的垂直于平面长度为 d 的方向向量：

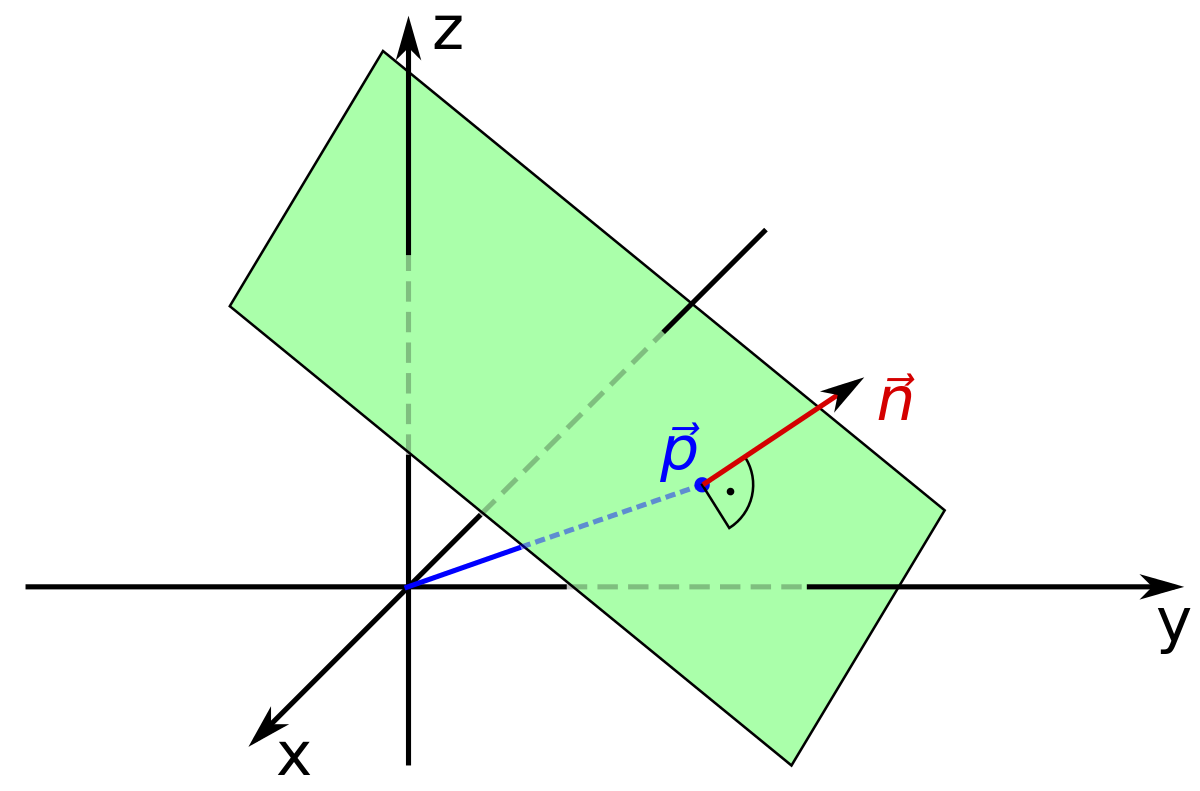
下面来看看 PxPlane 的 Transform 做了些什么：

• n：法向量不受平移影响，旋转操作直接和四元数 q 做乘法。
• d：平面到原点距离，不受旋转影响，但 Transform 的平移操作还需要结合平移方向 v 和旋转后的法向量 n 做投影来计算

$$p = d + \vec{v} \cdot \vec{n} = d + |v|cos\theta$$

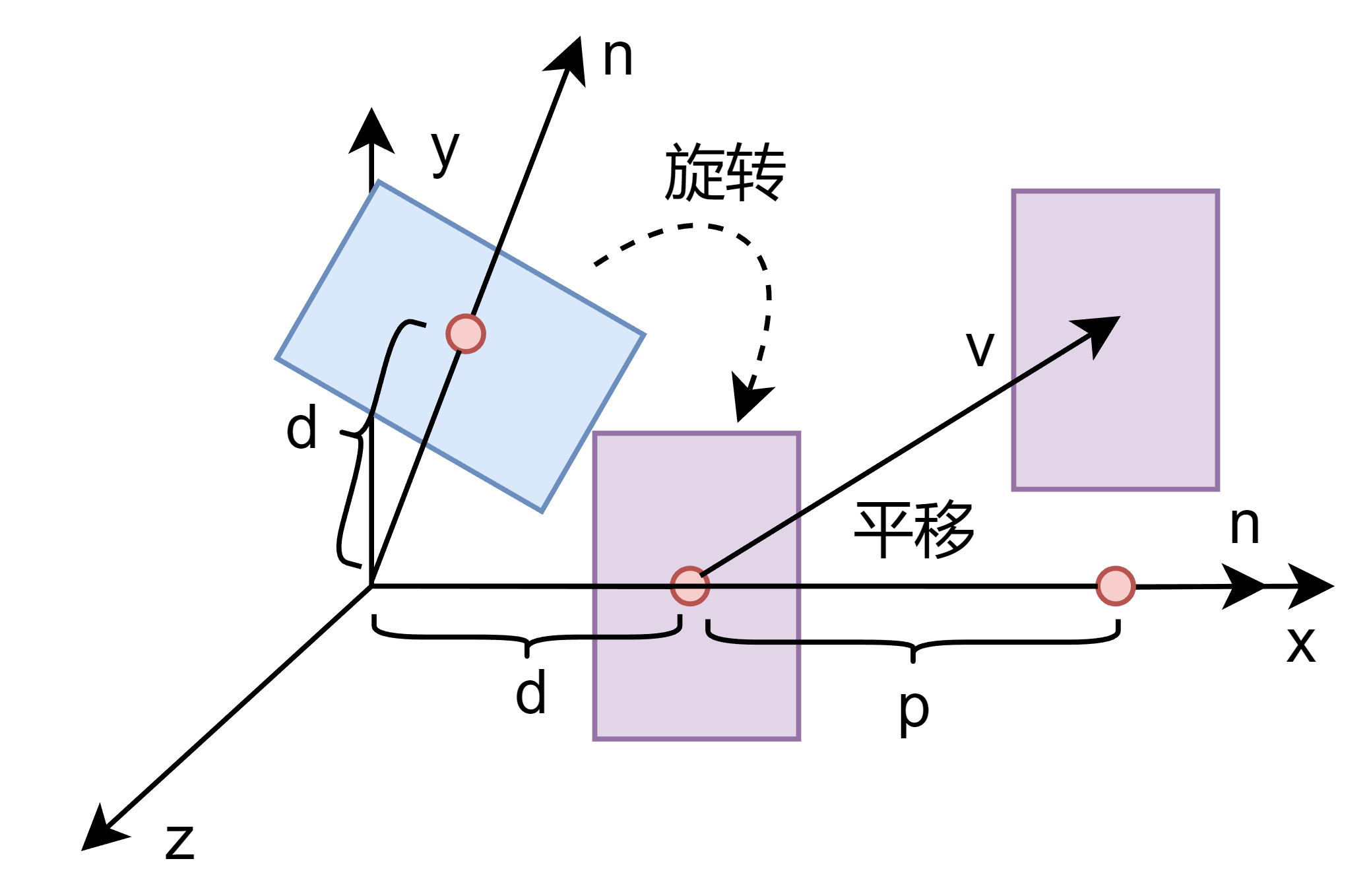
这里的结果来看，实际计算的距离是反的，因此可以推断法向量方向是从平面点指向原点。

PX_CUDA_CALLABLE PX_FORCE_INLINE PxPlane transform(const PxPlane& plane) const

{

    PxVec3 transformedNormal = rotate(plane.n);

    return PxPlane(transformedNormal, plane.d - p.dot(transformedNormal));

}

PX_CUDA_CALLABLE PX_FORCE_INLINE PxPlane inverseTransform(const PxPlane& plane) const

{

    PxVec3 transformedNormal = rotateInv(plane.n);

    return PxPlane(transformedNormal, plane.d + p.dot(plane.n));

}

# 参考链接

• Quaternion