以下为个人学习笔记整理。参考 PhysX SDK 3.4.0 文档,部分代码可能来源于更高版本。
# GJK && EPA
GJK 用来计算物体间的最短碰撞距离,而 EPA 用于计算物体发生嵌入的最短脱离距离,通过 GJK 和 EPA 可以知道物体是否嵌入,还需要运动多久发生碰撞。
# 基本概念
闵可夫斯基差(Minkowski difference)
也经常被称为「闵可夫斯基和」,简单来说就是两个集合的顶点两两做加法 (减法) 得到的新集合所组成的凸包。
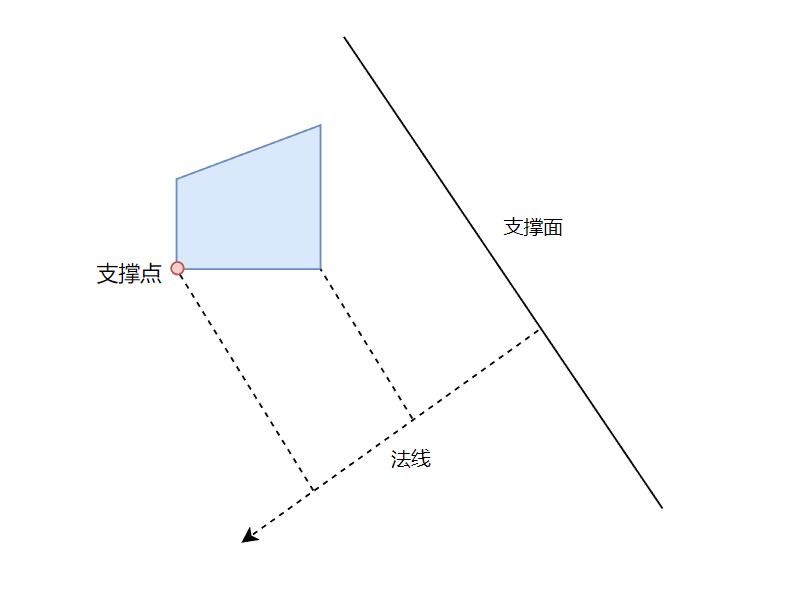
支撑面 && 支撑点
集合物体通过和支撑面的法线方向做投影所得到的最远距离点被称为支撑点。该点也可以理解为物体距离支撑面的最远点。
支撑函数
每个图形都有特定的支撑函数,该函数主要用来计算不同方向上的支撑点。
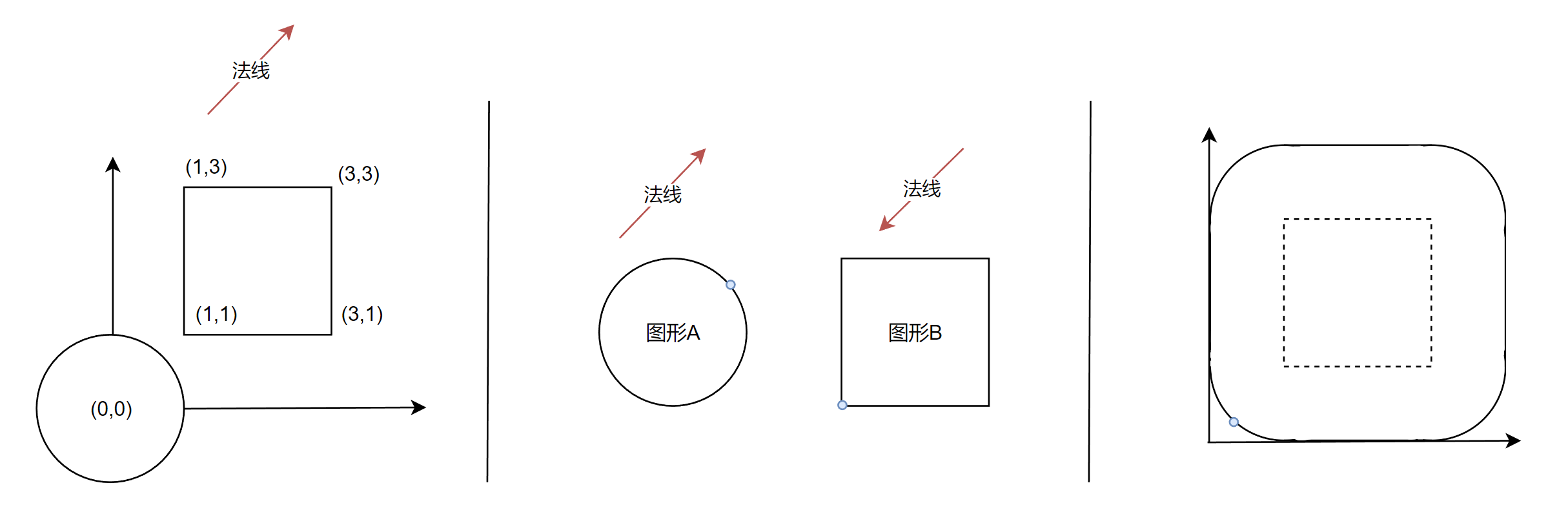
上述两个规则还可以进一步推演,计算某个指定(法线)方向的「闵可夫斯基差」的最远点(支撑点)。
两个图形分别取法线方向和法线反向计算支撑点,然后再做「闵可夫斯基差」:
# GJK(Gilbert–Johnson–Keerthi distance algorithm)
「闵可夫斯基差」可以用来描述两个物体间的距离,通过一个二维图形距离原点的距离进行表示(如果两个物体发送重叠,那么原点将会在该图形内部)。
由于「闵可夫斯基差」的特性,求解两个物体最近点可以简化为求解「闵可夫斯基差」点集组成的凸包中距离原点最近的点(前提是两个物体没有发生内嵌)
计算最短距离方法有点近似牛顿迭代法。本质上是通过多次迭代让结果趋于最优:
【step.1】取 「闵可夫斯基差」点集上的任意点,记作 ,由于该集合组成的图形是凸包,因此任意点都可以成为某个方向的支撑点。取 作为支撑面,沿着法线方向计算支撑点 。
【step.2】 和 组成的面支撑面记为 ,通过支撑面 计算新的法线(法线方向必须向着原点)这样才能距离原点更近,法线计算公式:,并得到新的支撑点 。
【step.3~4】取 和 中法线向着原点的作为新的支撑面计算新的支撑点 。
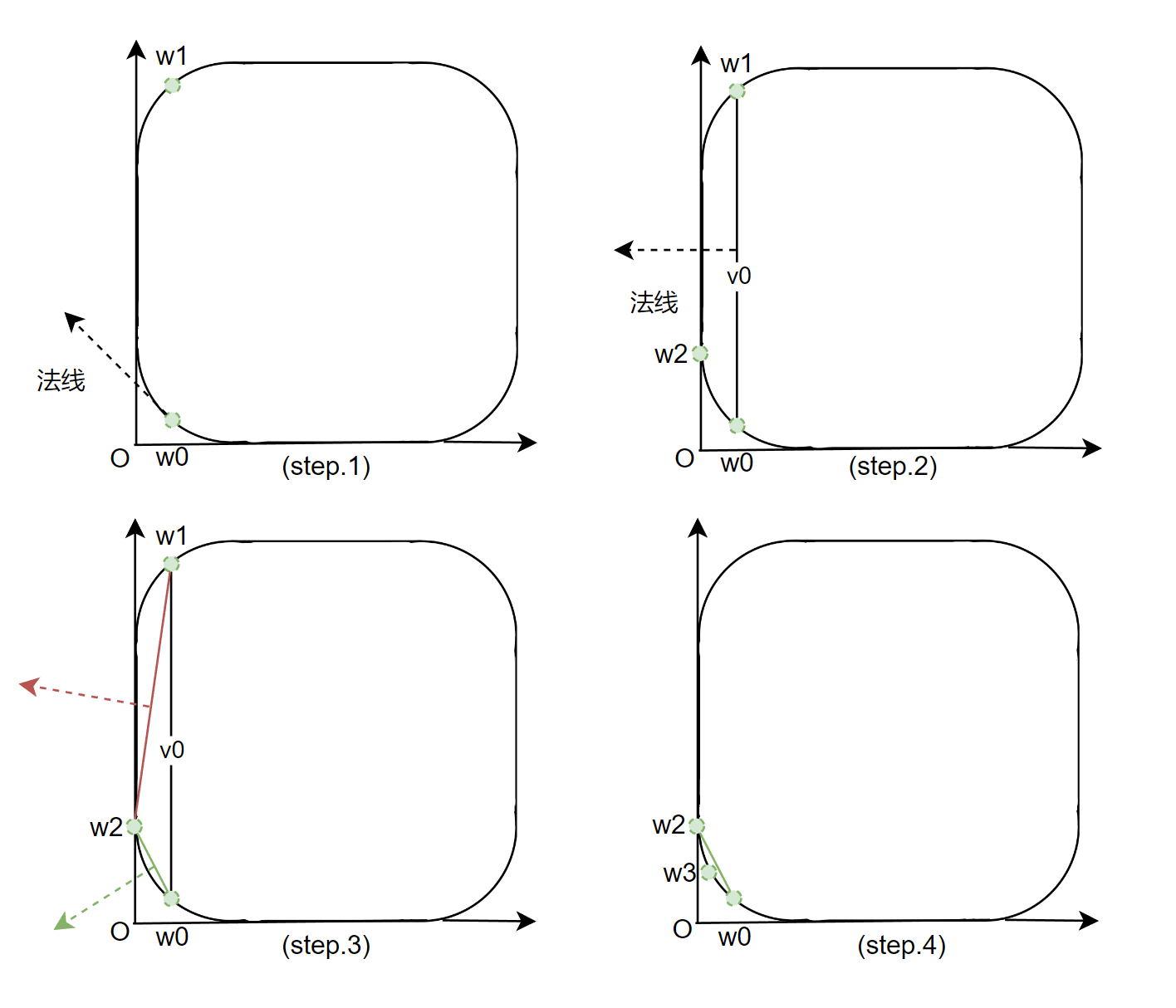
该迭代计算的退出条件有两个:
- 原点在当前三个支撑点组成的三角形内部,这种情况下说明物体发生了嵌入,GJK 计算失败,需要升级成 EPA 计算分离距离。
- 该迭代算法收敛到一定的阈值,例如 和原点距离近乎接近于 0 或者相比于上次迭代的距离变得更大,亦或者超过最大迭代次数等。
# EPA(Expanding Polytope Algorithm)
EPA 算法和 GJK 非常类似,GJK 是用于计算非重叠情况下两物体的最短距离,而 EPA 则是在此基础之上,计算重叠情况下的最小分离距离。
两着的思想也非常相似,计算最短距离依靠「闵可夫斯基差」求解各个方向上能够分离物体的最短距离,再从其中取最小值。
计算最小分离距离也是依靠「闵可夫斯基差」求解凸包集合中距离原点最近的位置,唯一的区别在于 GJK 求解中原点在凸包外部,而 EPA 求解时,原点在凸包内部。
由于 EPA 时 GJK 算法的特例,因此该算法会继承原有 GJK 算法的结果继续迭代,算法核心是构建一个 core shape,而最短脱离点则是该 core shape 中距离原点最近的点的距离:
【step.1】计算 GJK 过程中的失败情况下,会得到一个包含原点的三角形,通过把三角形三条边作为支撑面求解最短分离距离点。由于是求最短,因此分离距离大于当前距离的点集不会被纳入 core shape。
【step.2】由于新加入的点集又可以扩展出两个支撑面,重复上诉迭代步骤,没有更近的点被加入 core shape 集合时,该迭代就可以终止了。
【step.3】最后从得到的 core shape 中,找出距离原点最近的顶点即可。
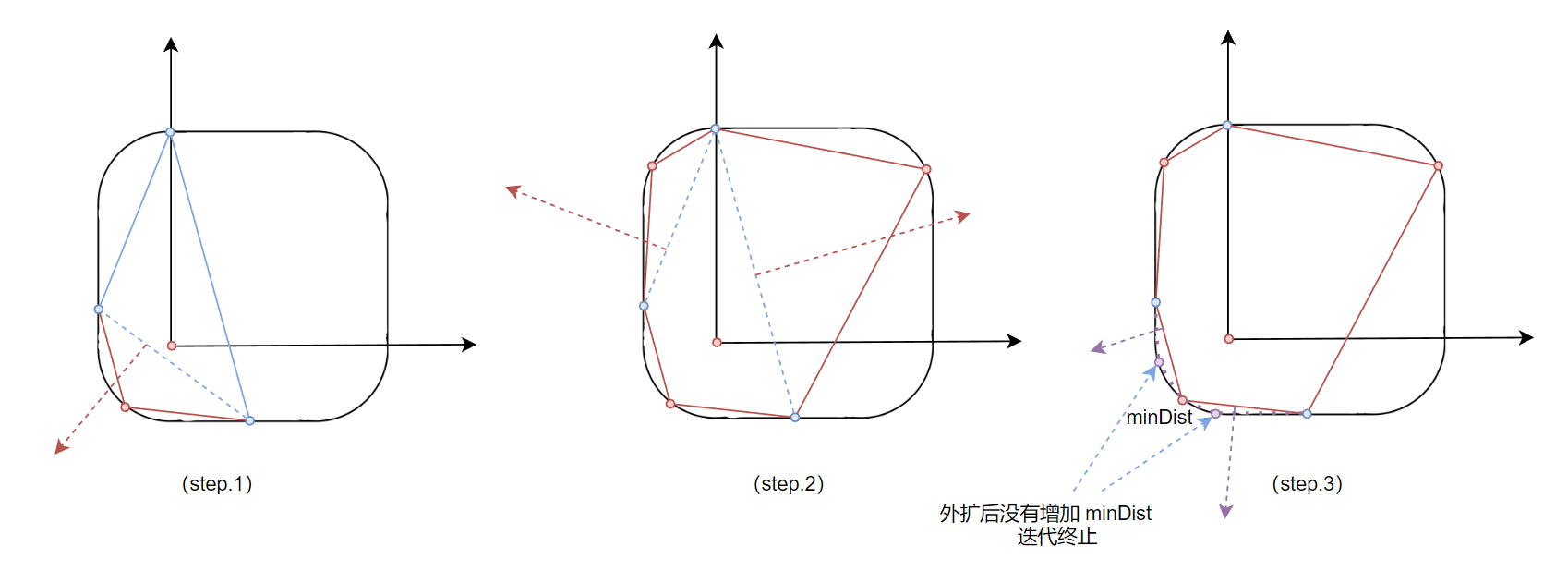
可以看到,整个算法对于点集较多的凸包 work 的不是很好,特别是圆形,算法结果收敛会变得很慢。
# Sweep 情况下如何计算碰撞点
对于静止物体我们可以直接套用 GJK && EPA 进行计算,得到最终的最短距离。那么对于运动中的对象如何获取到物体沿着某个方向运动的最长距离呢?
好消息是,一个物体对另一个物体进行 sweep 测试的过程中,「闵可夫斯基差」的形状是不会改变的,变化的只有「闵可夫斯基差」的「位置」。
利用这一特性,求解凸包的 EPA && GJK 就可以简化为求解一个拉伸「闵可夫斯基差」凸包的 EPA && GJK,看起来有点抽象,下面举个简单例子:
假设 「闵可夫斯基差」计算得到的最短方向正好和 sweep 方向是反向的,意味着 sweep 起始位置才是距离最近的,之后的运动都是远离物体的。因此 sweep 的影响可以被忽略。再延展一下,能够让 sweep 过程中两个物体靠的更近,就意味着 sweep 在「最短方向」上的水平分量是和「最短方向」同向的情况下。垂直方向自然是没有影响的,可以忽略。
这里假设 sweep 的方向为 。
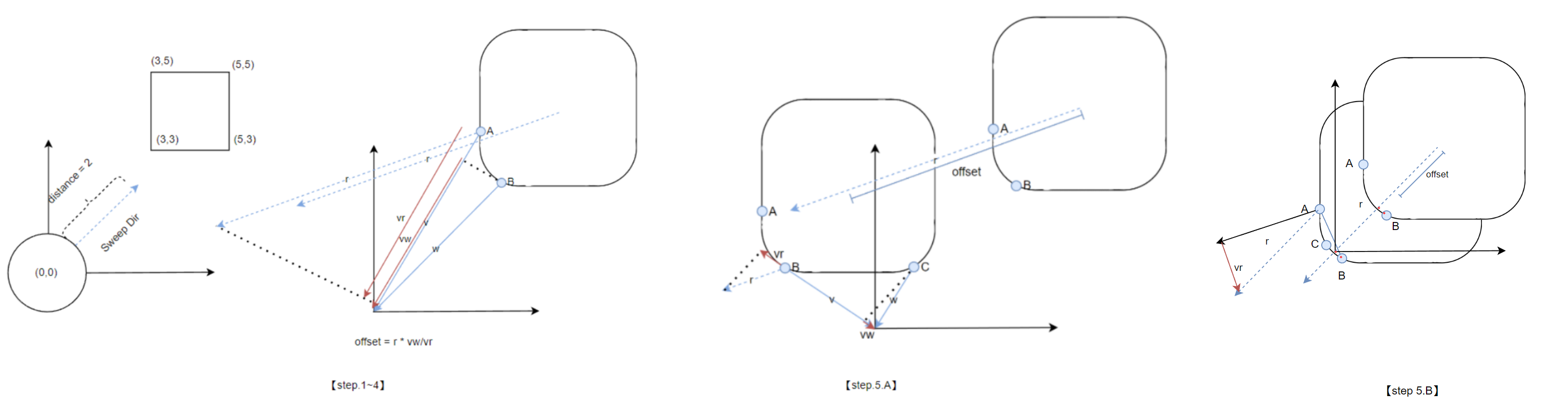
- 【step.1】找到任意一个支撑点 A,沿着 A 和原点方向作为法线寻找另一个支撑点 B。已知的是 B 肯定在 方向上离 O 点最近的支撑点。
- 【step.2】[设想一下,如果沿着 sweep 方向横扫,对于闵可夫斯基集合来说就意味着平移 。把 拆分成平行于 方向和垂直于 方向。垂直于 方向的 sweep 不会让 B 点到原点的距离变短(假设 B 在 AO 上有个投影 B’,B’ 一定是闵可夫斯基集合中沿着 AO 方向投影里,距离原点最近的点,又已知两点的距离表示集合图形的距离,那么垂直于 AO 移动 B’,肯定会让 B’ 变得更长,那么 B’O 也就更长,两个物体就会更加的远离)。
- 【step.3】那么唯一可能缩短距离的方向就还剩下平行于 方向的 sweep 分量。该 sweep 会让 B 点靠近原点。那么只需要确定,如果 B’O 的距离大于该分量,即便 sweep 到终点,也不会发生碰撞,反之则可能发生碰撞。我们可以求解这个分量(对 进行拆分,平行于 方向的记为 )。图中 是 B 点在 方向的投影,如果 小于 。则可能发生碰撞。
- 【step.4】如果可能碰撞的情况下,只需要步进一个 距离就可以还原 sweep 碰撞前的临界位置,求解出该距离对应的 sweep 方向所能够步进的最远距离
- 【step.5.A】如果不可能碰撞,只需沿着 方向对偏移后的新闵可夫斯基集差再做支持点查询,得到支撑点 C。同样计算出 。重复之前的「step1~4」 得到 sweep 对于 的投影 和 。如果 方向和 方向同向,且和 反向,那么可以预见,不论如何沿着 移动都不会缩两个图形短距离了,又已知垂直于 方向的移动也不会缩短距离,因此 sweep 方向的移动必然也不会再缩短距离,此时就视为无碰撞,计算结束。
- 【step.5.B】步进完成后,由于 垂直于 ,这里需要引入新的支撑点 C,C 的计算基于 方向法线。得到支撑点 C 后,问题退化为 EPA。由于此时已经发生重叠, 结果将为负数,sweep 的推进变为回退。回退一定距离后继续求解,直到达到临界值,便可求解得到 sweep 到达临界位置的最短距离。
# PhysX 的 GJK
PhysX 的 GJK 在查询和支撑点选取上做了一定的优化:
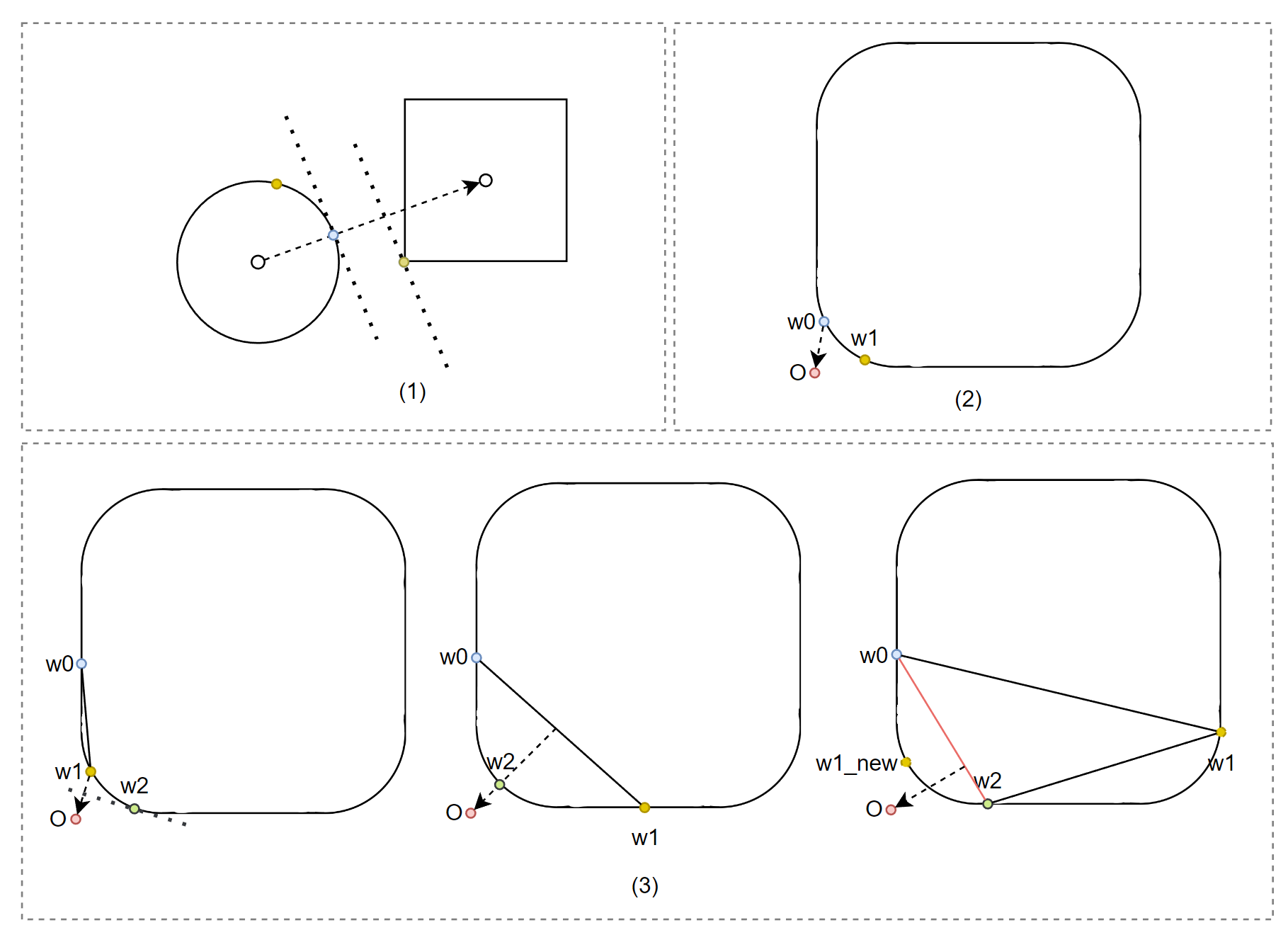
- 初始的支撑点 挑选方式是基于两个物体中心点的方向来做的。
- 第二个支撑点 是基于 方向作为法线求算得到。
- 后续支撑点的计算方向有两套规则:
- 支撑点只有两个的情况下,计算原点和两支撑点组成线段的最短距离位置。并得到该位置到原点的方向作为查询方向。
- 支撑点有三个的情况下,计算三个支撑点组成的三角形和原点的最短距离位置(最短边 )。然后用该位置到原点的方向作为查询方向得到新的支撑点用于替换 。
# 对于球体和胶囊体,如何在有限的迭代中得到最优解
计算中引入了一个「膨胀的概念」Unreal 中称为 「Thickness」,PhysX 中称为「Inflation」。这个概念对应求解球体和胶囊体非常有效,有了这个「膨胀值」球体就可以表示成一个「点」,而胶囊体就是一个线段,在计算碰撞的时候,只需要对点和线段做检查,并在结果中加入一个膨胀值即可。
# 参考链接
- A Fast and Robust GJK Implementation for Collision Detection of Convex Objects
- 可视化的 GJK 计算页面
- A Strange But Elegant Approach to a Surprisingly Hard Problem (GJK Algorithm)
- Real-time Collision Detection with Implicit Objects
- Collision Detection in Interactive 3D Environments