# 「Scene Queries」AABBTree—— 下

下篇主要介绍 AABBTree 的增量版本 ——IncrementalAABBTree。阅读本文之前建议请先了解 「Scene Queries」AABBTree—— 上，不然很可能看的迷迷糊糊 (～￣▽￣)～

IncrementalAABBTree 相比于 AABBTree 最大的区别在于支持了插入删除时能够动态更新树结构（旋转操作，并且由于动态特性，一定程度上简化了数据结构，没那么扣扣嗖嗖了～

# IncrementalAABBTree 数据组成

比较简单，只有四个结构：

Ps::Pool<AABBTreeIndices>                   mIndicesPool;

Ps::Pool<IncrementalAABBTreeNodePair>       mNodesPool;

IncrementalAABBTreeNode*                    mRoot;

NodeAllocator                               mNodeAllocator;

• mIndicesPool：AABBTree.mIndices 的池化版本，支持动态增删，至于 AABBTreeIndices，稍后再做介绍。
• mNodesPool：和 AABBTree.mRuntimePool 比较相似，都是存储最终构建的结果，不过为了支持动态增删做了一定程度的妥协，所以内存布局没那么紧凑，IncrementalAABBTreeNodePair 就是两个 IncrementalAABBTreeNode 的结构体。
• mRoot：根节点。
• mNodeAllocator：参考 AABBTree，功能用法完全一致。

# AABBTreeIndices

struct AABBTreeIndices

{

    PxU32               nbIndices;

    PoolIndex           indices[NB_OBJECTS_PER_NODE];

};

• nbIndices：记录节点内包围盒数量，有点类似 AABBTreeBuildNode.mNbPrimitives。
• indices：记录每个包围盒对应于 AABBTreeBuildParams.mAABBArray 中下标。

# IncrementalAABBTreeNode

功能上和 AABBTreeRuntimeNode 近似，表示 IncrementalAABBTree 最小单位。不过节点大小是 AABBTreeRuntimeNode 的两倍（28 vs 56）。

• mBVMax && mBVMin：节点包围盒数据。

• mParent：父节点指针。

• mChilds[2] / mIndices：union 类型。如果是非叶节点情况下，通过 mChilds[2] 指向左右子节点；如果是叶节点通过 mIndices 标识包围盒所在位置。辨别是否为叶节点可以通过 mChilds[1] 是否为 0 判定，因为两者都是指针类型，mIndices 只用到了第一个指针因此第二个是空缺的。

# IncrementalAABBTree 构建流程

IncrementalAABBTree 构建流程和 AABBTree 几乎一样，都是通过 AABBTreeBuildNode 的 _buildHierarchy 函数实现。具体细节可以参考 AABBTree—— 上，这里不再赘述。构建完成后有一个 clone 操作。

# clone

这一步主要是把 AABBTreeBuildNode 树形结构转为 IncrementalAABBTreeNode 树形结构，有点和 flatten 相同的意味。顺带还会生成一个 map 结构，用来映射 mAABBArray 下标和 IncrementalAABBTreeNode 对应叶节点指针，和 AABBTreeUpdateMap 比较相近。

# IncrementalAABBTree 结构图

最终构建完成后，mNodesPool 存储所有节点信息，叶节点还会关联到 mIndicesPool 中的 AABBTreeIndices，由于每个叶节点最多存储 4 个包围盒信息，因此 AABBTreeIndices 中又记录了每个包围盒的 bounds 下标。

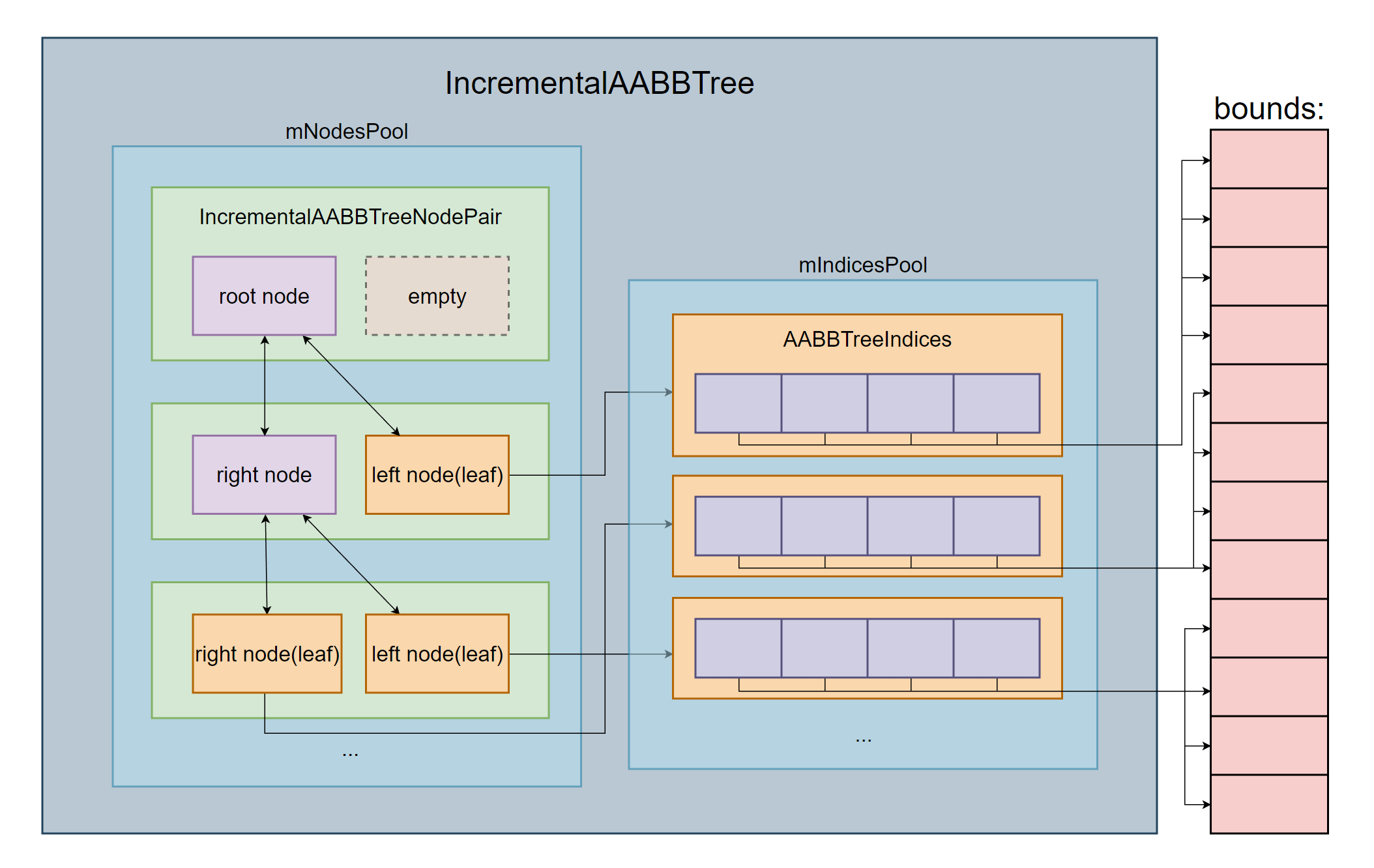
# IncrementalAABBTree 增删改

IncrementalAABBTree 的增删改操作本身并不复杂，但是为了提高二叉树的查找效率，在变更二叉树节点的同时还需要考虑树的平衡性。

因此在介绍增删改之前，先来看看 IncrementalAABBTree 如何平衡化的：

# IncrementalAABBTree 平衡性

如何衡量一棵树是否平衡？常规的二叉树通过树的左右子树层级作为指标，如果两者层级相差超过一层则进行平衡（rotate）。

不过 AABBTree 的划分标准有所不同：由于 AABBTree 的构建是基于包围盒包含关系来的，因此平衡性的标准也需要有所调整。为了尽可能保证查找时所有叶节点命中的概率尽可能相似，使得 AABBTree 在抽象层面更加扁平。而查找的命中和 AABB 节点包围盒的「体积」成正相关，因此体积大小就成了衡量 AABBTree 平衡的标准。

# 相关概念

在介绍平衡性和旋转之前，先了解一些名字术语：

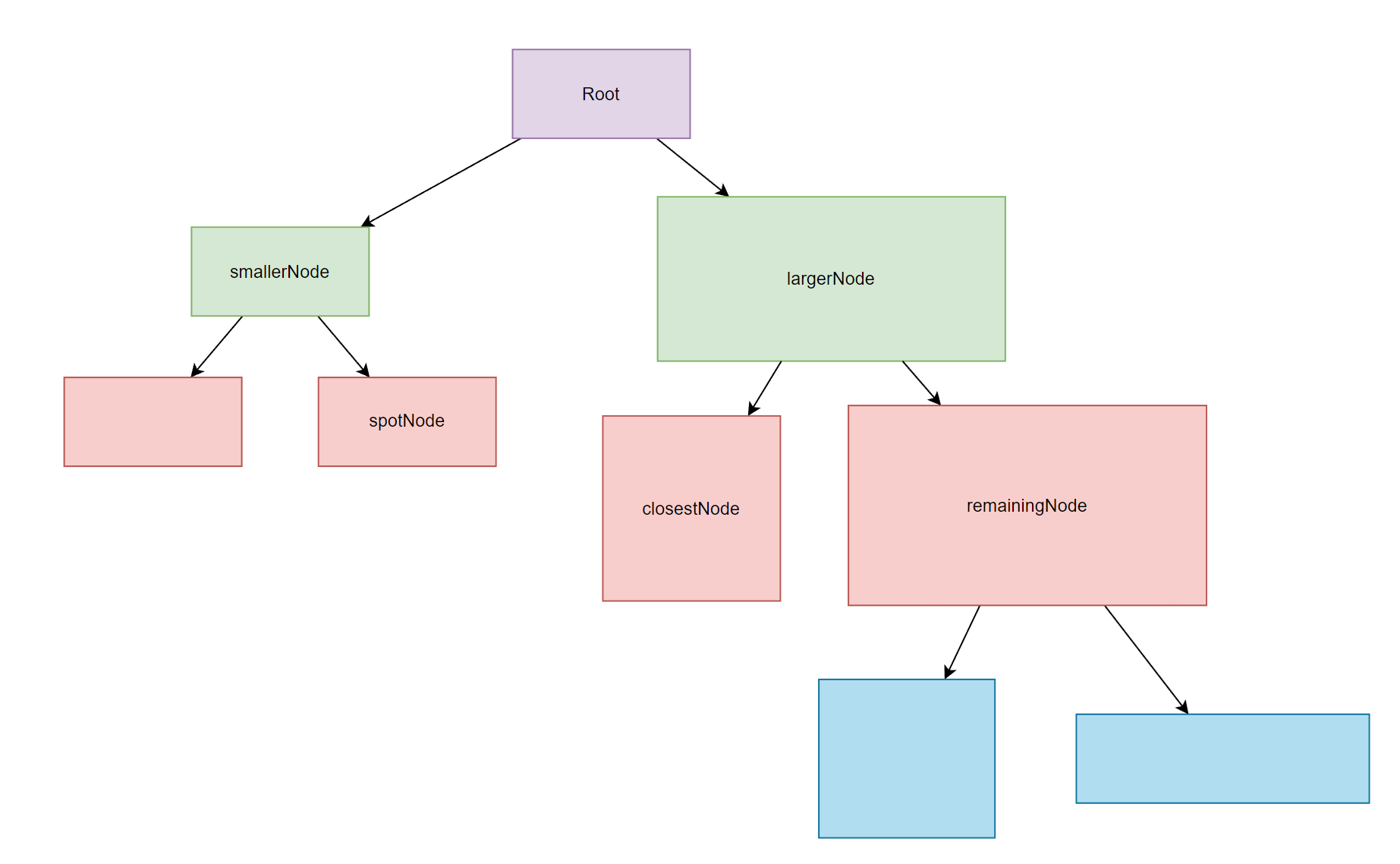
• largerNode && smallerNode：通常情况下，两个兄弟节点里其中一个的体积如果超过另一个的 3 倍，那么就把体积大的称为 largerNode，体积小的称为 smallerNode。
• closestNode && remainingNode：如果已知一个 largerNode 和 smallerNode，那么 largerNode 中最靠近 smallerNode 的叶节点被称为 closestNode ，而 closestNode 的兄弟节点则叫做 remainingNode。
• spotNode：表示 smallerNode 中最靠近 closestNode 的叶节点。

# traversalDirection && rotateTree

traversalDirection 操作用于检测两个兄弟节点是否平衡，并且计算出兄弟节点中距离测试点最近的和体积较大的。

PX_FORCE_INLINE static PxU32 traversalDirection(const IncrementalAABBTreeNode& child0, const IncrementalAABBTreeNode& child1, const Vec4V& testCenterV,

	bool testRotation, bool& rotateNode, PxU32& largesRotateNode)

{

	// traverse in the direction of a node which is closer

	// we compare the node and object centers

	const Vec4V centerCh0V = V4Add(child0.mBVMax, child0.mBVMin);

	const Vec4V centerCh1V = V4Add(child1.mBVMax, child1.mBVMin);

	const Vec4V ch0D = V4Sub(testCenterV, centerCh0V);

	const Vec4V ch1D = V4Sub(testCenterV, centerCh1V);

	if(testRotation)

	{

		// if some volume is 3x larger than we do a rotation

		const float volumeCompare = 3.0f;

		PX_ALIGN(16, PxVec4) sizeCh0;

		PX_ALIGN(16, PxVec4) sizeCh1;

		const Vec4V sizeCh0V = V4Sub(child0.mBVMax, child0.mBVMin);

		const Vec4V sizeCh1V = V4Sub(child1.mBVMax, child1.mBVMin);

		V4StoreA(sizeCh0V, &sizeCh0.x);

		V4StoreA(sizeCh1V, &sizeCh1.x);

		const float volumeCh0 = sizeCh0.x*sizeCh0.y*sizeCh0.z;

		const float volumeCh1 = sizeCh1.x*sizeCh1.y*sizeCh1.z;

		if((volumeCh0*volumeCompare < volumeCh1) || (volumeCh1*volumeCompare < volumeCh0))

		{

			largesRotateNode = (volumeCh0 > volumeCh1) ? 0u : 1u;

			rotateNode = true;

		}

	}

	const BoolV con = FIsGrtr(V4Dot3(ch0D, ch0D), V4Dot3(ch1D, ch1D));

	return (BAllEqTTTT(con) == 1) ? PxU32(1) : PxU32(0);

}

rotateTree 用来对树进行旋转。旋转的大体流程可以分为以下几个步骤：

• 【step.1】找出 largerNode 中最靠近 smallerNode 的叶节点 closestNode。
• 【step.2】找出 smallerNode 中最靠近 closestNode 的叶节点 spotNode。
• 【step.3】把 closestNode 合并到 spotNode，并调整 remainingNode 和 largerNode 的父子关系。到此第一步旋转就算完成了～
• 【step.4】由于 spotNode 合并了 closestNode 后体积发生了较大变化，因此需要对 smallerNode 整体做个扫描，判定需不需要再旋转一次。如果需要的话，重复【step.1~3】。

调整 remainingNode 和 largerNode 的父子关系可能出现两种情况：

• remainingNode 是叶节点。
• remainingNode 是非叶节点。

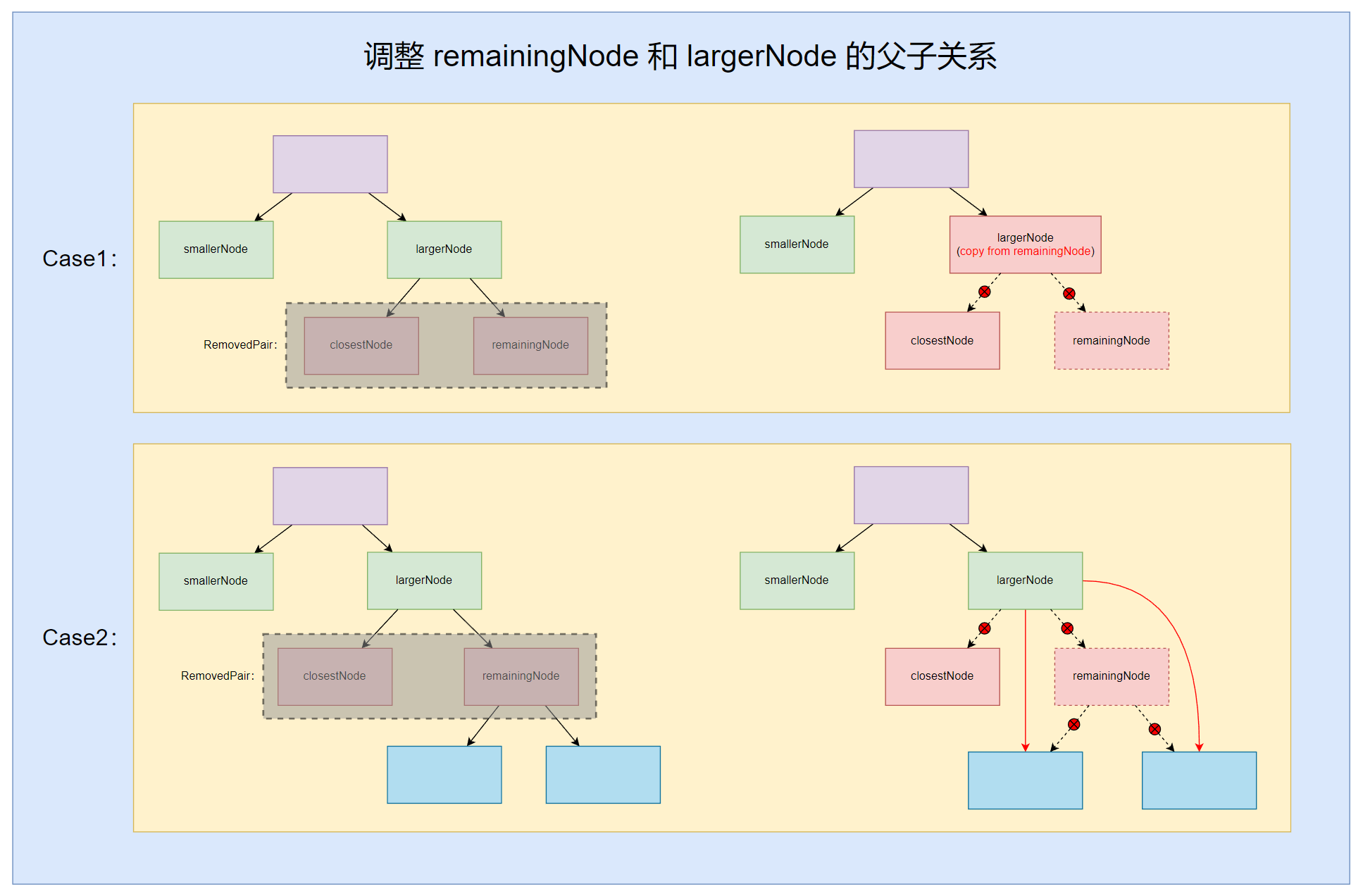
把 closestNode 合并到 spotNode 同样也存在两种情况：

• spotNode 合并了 closestNode 之后容量没超过上限。
• spotNode 合并了 closestNode 之后容量超过上限。

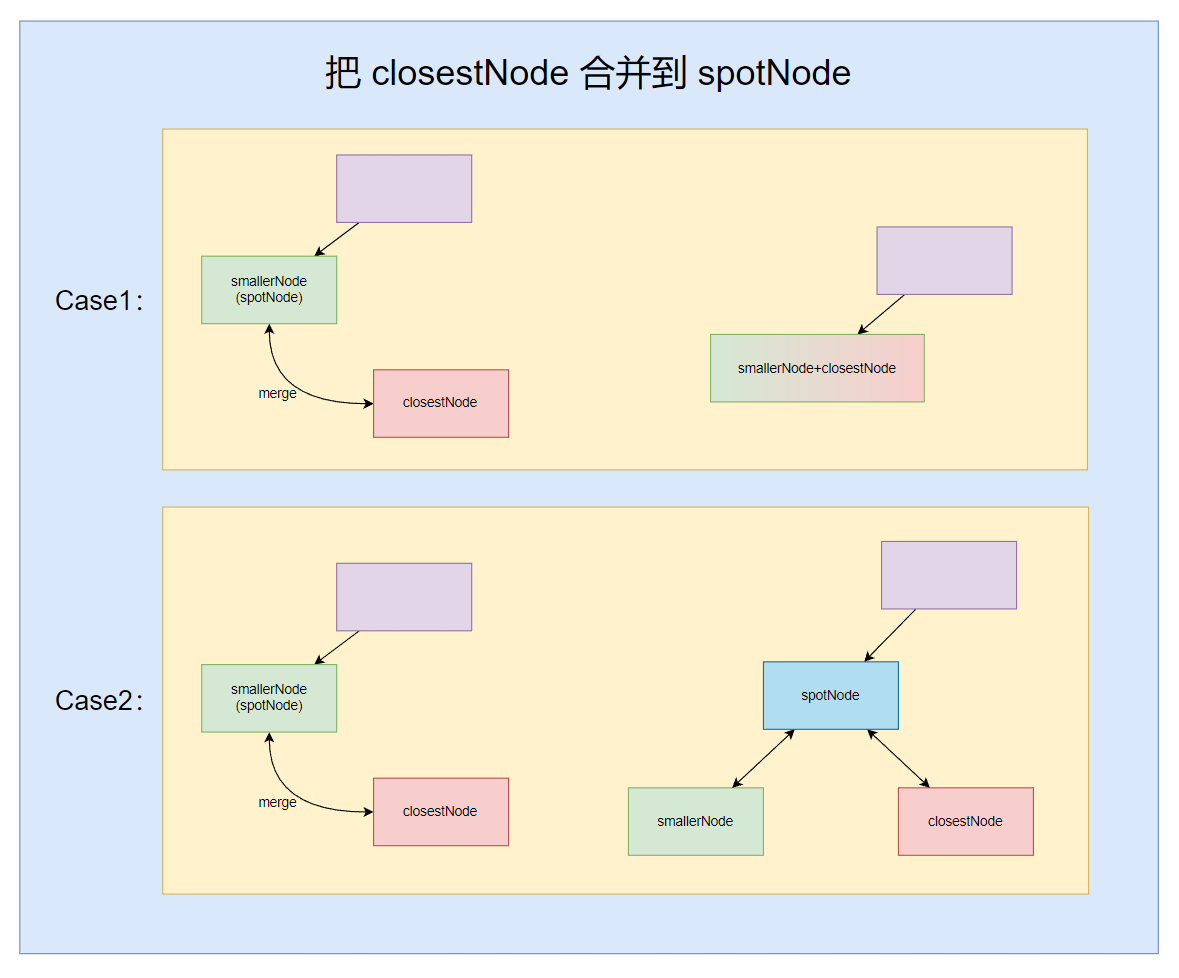
讨论完 rotateTree，整个增删改操作就变得较为简单：

• 增：查询距离插入包围盒最近叶节点进行插入，有点类似节点合并。插入完成后如果发现节点需要平衡化，还会进行一次 rotateTree。
• 删：删除其实更为简单，前面提到构建时有一个 map 映射，可以直接定位到对应叶节点进行删除，如果叶节点删除后为空，则再执行一次树结构调整，把兄弟节点替换掉父节点即可。
• 改：该操作有两种模式 update && updateFast 。更新操作本质上是「删」、「增」操作的组合。 updateFast 则是先对变更后的包围盒和原本的叶节点包围盒做一次相交性检查，如果相交的情况，则仅更新包围盒大小，不调整节点排布，应该是为了应对包围盒在小范围内移动的情况下，导致 IncrementalAABBTree 频繁增删而做的优化。

# 总结

到此，IncrementalAABBTree 也介绍完毕了。AABBTree 追求极致的内存占用，在很多方面都精打细算，像一个精致的艺术品；而 IncrementalAABBTree 为了实现动态变化的灵活，频繁的增删改。牺牲了部分性能、提高了内存占用，但也在一定程度上简化了编码，像一个乐高玩具。两者可谓是各有优劣。