首页 学习 物理引擎

以下为个人学习笔记整理。参考 PhysX SDK 3.4.0 文档，部分代码可能来源于更高版本。

# 「Scene Queries」AABBTree—— 上

AABBTree 是 PhysX 用来实现场景查询的基本数据结构，通过 AABBTree 可以实现高效的 AABB 粗筛，从而提高物理检测的查询效率。

之所以把 AABBTree 单独拎出来说，主要是因为其涵盖的内容较多。当作一个单独的篇幅来展开讨论完全合适～

# AABBTree 中的数据组成

AABBTree 中的类变量总计有十个：

PxU32*                  mIndices;
PxU32                   mNbIndices;
AABBTreeRuntimeNode*    mRuntimePool;
NodeAllocator           mNodeAllocator;
PxU32*                  mParentIndices;
PxU32                   mTotalNbNodes;
PxU32                   mTotalPrims;
FIFOStack*              mStack;
BitArray                mRefitBitmask;
PxU32                   mRefitHighestSetWord;
  • mNbIndices && mIndices：「mIndices」是一个索引数组，而「mNbIndices」表示该数组的长度。
  • mRuntimePool：用来存储 AABBTree 运行过程中的所有节点数据。
  • mNodeAllocator：用来管理 AABBTree 构建过程中的节点分配。
  • mParentIndices：用来映射运行过程中节点的父节点索引。
  • mTotalNbNodes && mTotalPrims：分别指代 AABBTree 中的总节点数量和总包围盒数量。
  • mStack：一个先进先出的队列，用来实现分布式构建的临时存储结构。
  • mRefitBitmask：Bit 数组，数组长度最大为 2^27，数组内每个元素都是 UInt32 类型。
  • mRefitHighestSetWord：类似于脏标记，用来记录变更节点的最大下标。

# AABBTree 的构建流程

AABBTree 的构建有三个模式：

  • 全量同步构建
  • 全量分布构建

# 全量同步构建（build）

全量同步构建，顾名思义在一帧内完成整棵树的构建工作：

bool AABBTree::build(AABBTreeBuildParams& params)
{
	// Init stats
	BuildStats stats;
	if(!buildInit(params, stats))
		return false;
	// Build the hierarchy
	mNodeAllocator.mPool->_buildHierarchy(params, stats, mNodeAllocator, mIndices);
	buildEnd(params, stats);
	return true;
}
「build」主要可以分为三个阶段：
  • buildInit ：初始化构建环境。
    • 基础数据计算。这里主要是提前计算好所有参与构建的包围盒中心点坐标用来提高后面做切分的效率。
    • 内存消耗的预估和预分配。提前计算好可能需要的节点数并预先分配好内存池大小，顺带初始化根节点。
  • _buildHierarchy ：构建流程的核心，下面再展开介绍。
  • buildEnd ：构建完成后收尾工作。
    • 把构建数据转为运行时数据。主要是对数据做一个压缩。
# 初始化构建环境（buildInit）
初始化环境的代码总体比较简单，但有一个参数非常的关键 ——AABBTreeBuildParams。
class AABBTreeBuildParams : public Ps::UserAllocated
{
    PxU32			mLimit;			
    PxU32			mNbPrimitives;	
    const 			PxBounds3*		mAABBArray;		
    PxVec3*			mCache;			
};
AABBTreeBuildParams 提供了构建 AABBTree 所需的全部「原材料」和「构建参数」：
  • mLimit：指定 AABBTree 叶节点所能存放的包围盒最大数量，默认是 4 个。如果超过 mLimit，则该节点就必须继续拆分。
  • mNbPrimitives && mAABBArray：表示「原材料」的数量和原材料数组的首地址指针。这里的「原材料」就是参与构建的物体的 AABB 包围盒。
  • mCache：Vec3 的数组，用来缓存每个 AABB 包围盒的中心点，在「初始化构建环境」时会被计算并赋值。
另外还有三个 AABBTree 成员被初始化：mNbIndices、mIndices、mNodeAllocator。mNbIndices、mIndices 暂且先不介绍，先来看看 mNodeAllocator。
# NodeAllocator
NodeAllocator 是整个 AABBTree 构建中比较重要的类，它主要负责在 AABBTree 构建过程中申请和分配内存用来创建构建节点。
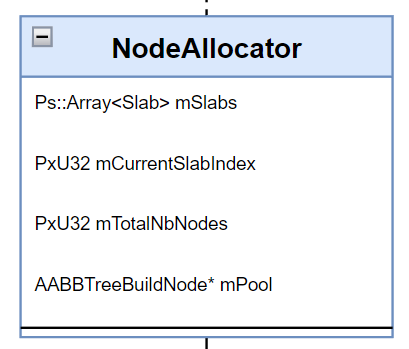
  • mSlabs：Slab 的数组
  • mCurrentSlabIndex：当前正在使用的 Slab 的下标
  • mTotalNbNodes：所有 Slab 数组中的节点总和
  • mPool：当前正在使用的 Slab 的节点内存池
为了进一步了解该类的作用，还得从 Slab 和 AABBTreeBuildNode 两个结构下手：
# Slab
Slab 是一个 AABBTreeBuildNode 的节点池，记录了 AABBTreeBuildNode 数组的首地址、已经分配出去的节点数以及可分配的最大节点数。
struct Slab
{
    AABBTreeBuildNode*  mPool;
    PxU32               mNbUsedNodes;
    PxU32               mMaxNbNodes;
};
# AABBTreeBuildNode
AABBTreeBuildNode 则是构建 AABBTree 时的最小单位：
这里暂时先看其类成员，函数我们后面再来介绍：
  • mBV：记录该节点的包围盒大小。这里分两种情况：
    • 如果该节点为叶节点。它的包围盒大小是其所包含的所有对象的包围盒的并集。
    • 如果该节点为非叶节点。它的包围盒大小是其左右子树的包围盒并集。
  • mPos：指向其左子树节点的位置。
  • mNodeIndex：这个变量比较特殊，它需要关联上 AABBTree.mIndices 来使用，这个我们后面再介绍。
  • mNbPrimitives：表示该节点内所包含的包围盒对象数量，如果是非叶节点则对象数量为所有子节点的总和。
介绍完 Slab 和 AABBTreeBuildNode，对于 NodeAllocator 我们也就有一个大概的轮廓了。NodeAllocator 实际上是一个节点内存池的池数组，在我们构建 AABBTree 需要创建新的 AABBTreeBuildNode 的时候，NodeAllocator 会先从当前正在使用的 Slab 中的节点池来获取节点，如果节点池已经没有空闲节点了，就会再创建一个新的 Slab，并使用新的 Slab 中的节点池（一个节点池最多会存在 1024 个空闲节点）用于分配节点。
# 构建 AABBTree（_buildHierarchy）
总算到 AABBTree 构建了，整个构建的实现都在 AABBTreeBuildNode 的两个接口中 ——_buildHierarchy && subdivide。
大致实现：尝试切分当前节点，切分成功递归切分，知道达到 mLimit 的要求则结束。
void AABBTreeBuildNode::_buildHierarchy(AABBTreeBuildParams& params, BuildStats& stats, NodeAllocator& nodeBase, PxU32* const indices)
{
	// Subdivide current node
	subdivide(params, stats, nodeBase, indices);
	// Recurse
	if (!isLeaf())
	{
		AABBTreeBuildNode* Pos = const_cast<AABBTreeBuildNode*>(getPos());
		PX_ASSERT(Pos);
		AABBTreeBuildNode* Neg = Pos + 1;
		Pos->_buildHierarchy(params, stats, nodeBase, indices);
		Neg->_buildHierarchy(params, stats, nodeBase, indices);
	}
	stats.mTotalPrims += mNbPrimitives;
}
subdivide 实现的切分相对复杂一些：
  • 根据当前节点包含的所有包围盒，计算当前节点的包围盒，顺便还能算一个所有包围盒的均值
  • 判断拆分条件，满足的话进行拆分：
    • AABBTree 的拆分基于方差，这里会算出所有包围盒和均值的方差，x、y、z 轴的方差分开计算的。最后会选择方差最大的作为本次的拆分轴
    • 拆分的启发函数比较简单，就是直接对半砍，大放左边，小的放右边。拆分过程势必需要做排序，AABBTree 构建选用的是快排。但有点需要注意，由于源数据是个包围盒数组（AABBTreeBuildParams.mAABBArray），他可能是别的上层应用长期使用的数据，并非临时用于构建的，因此在构建中修改源数据是非常危险的，这里采用了一个比较巧妙的做法 —— 二级索引。简单来说就是对包围盒数组做了一次再映射，用一个额外的数组来记录 mAABBArray 的下标，这样如果需要变化数组位置的时候，实际上可以仅调换二级索引而不修改源数据。而这个二级索引就是我们之前提到的 AABBTree.mIndices。
    • 如果基于启发函数的拆分导致最终所有包围盒都在同一边，则会进行暴力的对半分。
    • 拆分完毕后，通过 NodeAllocator 分配两个 AABBTreeBuildNode 作为当前节点的左右子树并分别记录各自节点所包含的包围盒起始位置及数量。
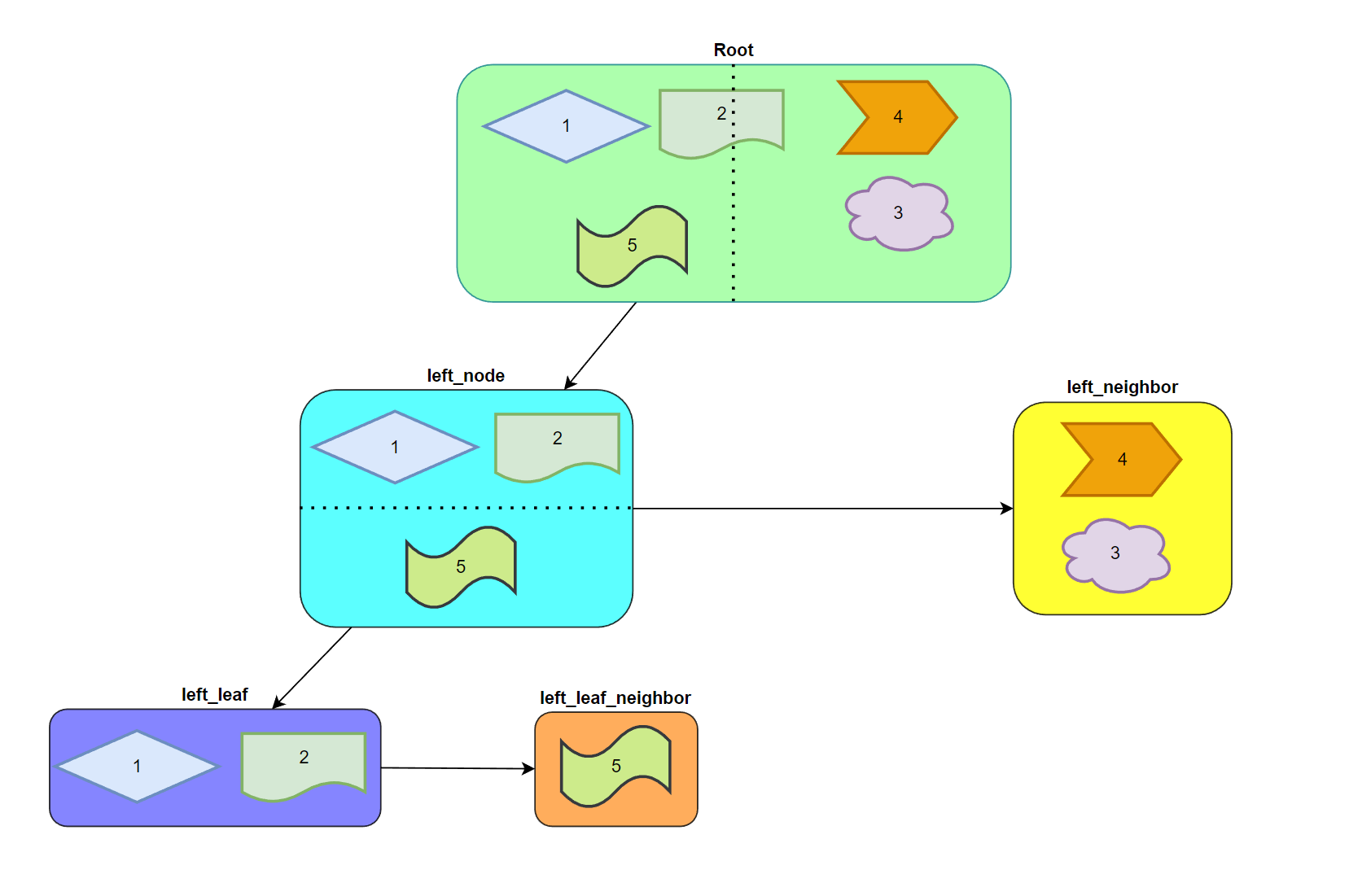
# 拆分简图
例如最顶层是所有参与 AABBTree 构建的几何，假设我们的 mLimit 为 2，也即是超过 2 个几何的节点就需要进行拆分：
  • 第一次针对 y 轴做了一次拆分，因此整棵树被分成了两半：left_node、left_neighbor。
  • left_neighbor 已经满足要求可以不需要拆分了，接下来我们继续对 left_node 做拆分。
  • left_node 的拆分是沿着 x 轴进行，同样也把整棵树分成了两半：left_leaf、left_leaf_neighbor。
  • 到此整个拆分就结束了，整棵树看起来就像下面这张图一样。
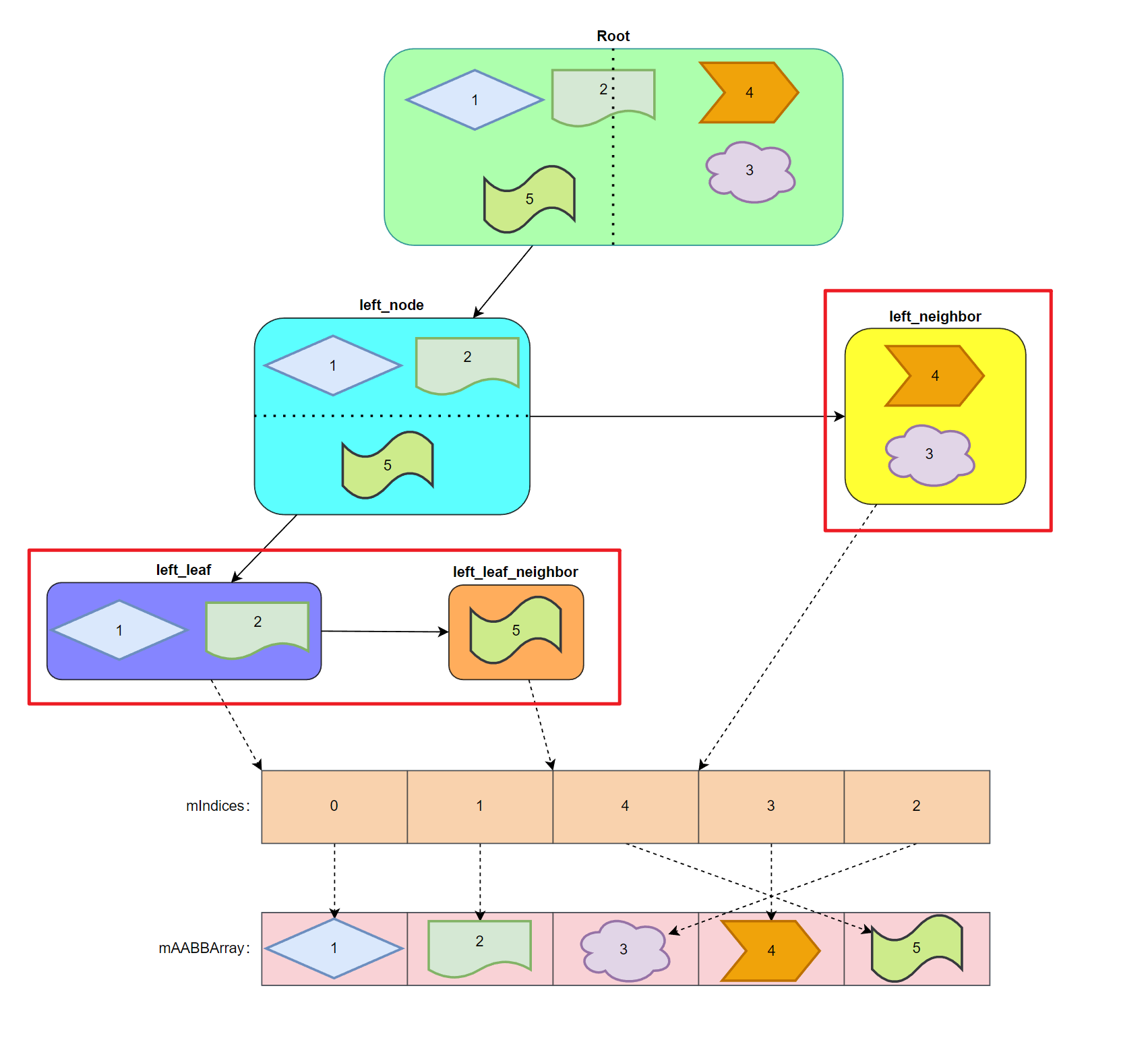
让我们回到之前 AABBTreeBuildNode.mPos 的部分以及没有提到的 AABBTree.mIndices。可以想象一下，所有包围盒都是存储在列表 AABBTreeBuildParams.mAABBArray 内的，那么上面抽象的拆分如何用数据的形式存储呢？
实际上 AABBTreeBuildNode 内会保存其所包含的所有包围盒的并集信息，但并不会保存每个对象的包围盒信息，而是记录下它在 AABBTree.mIndices 里的下标和范围。
刚才也提到，为了不修改源数据，因此做了二级映射（AABBTree.mIndices）来存储排序后的下标数据，这样就可以通过 AABBTree.mIndices 里存储的下标去 mAABBArray 内拿到对应的包围盒数据了～
image-20220817142717771
另外 AABBTreeBuildNode 是如何存储的，也是个让人不得不在意的话题，由于所有的 AABBTreeBuildNode 都通过 NodeAllocator 进行分配，而 NodeAllocator 内部其实是一个对象池数组，因此可以视为二维数组，再简化一下可以展开成一维数组。
前面说到 AABBTreeBuildNode 的 mPos 会存储左子树指针，那么右子树如何获取的呢？由于每次拆分后的两个节点（左右子节点）会在同一个操作内被申请和创建，因此两个节点实际上对应到数组内是紧挨着的，因此可以通过左子树偏移 1 个单位获取右子树：
image-20220817143833110
# 构建结果压缩（buildEnd）
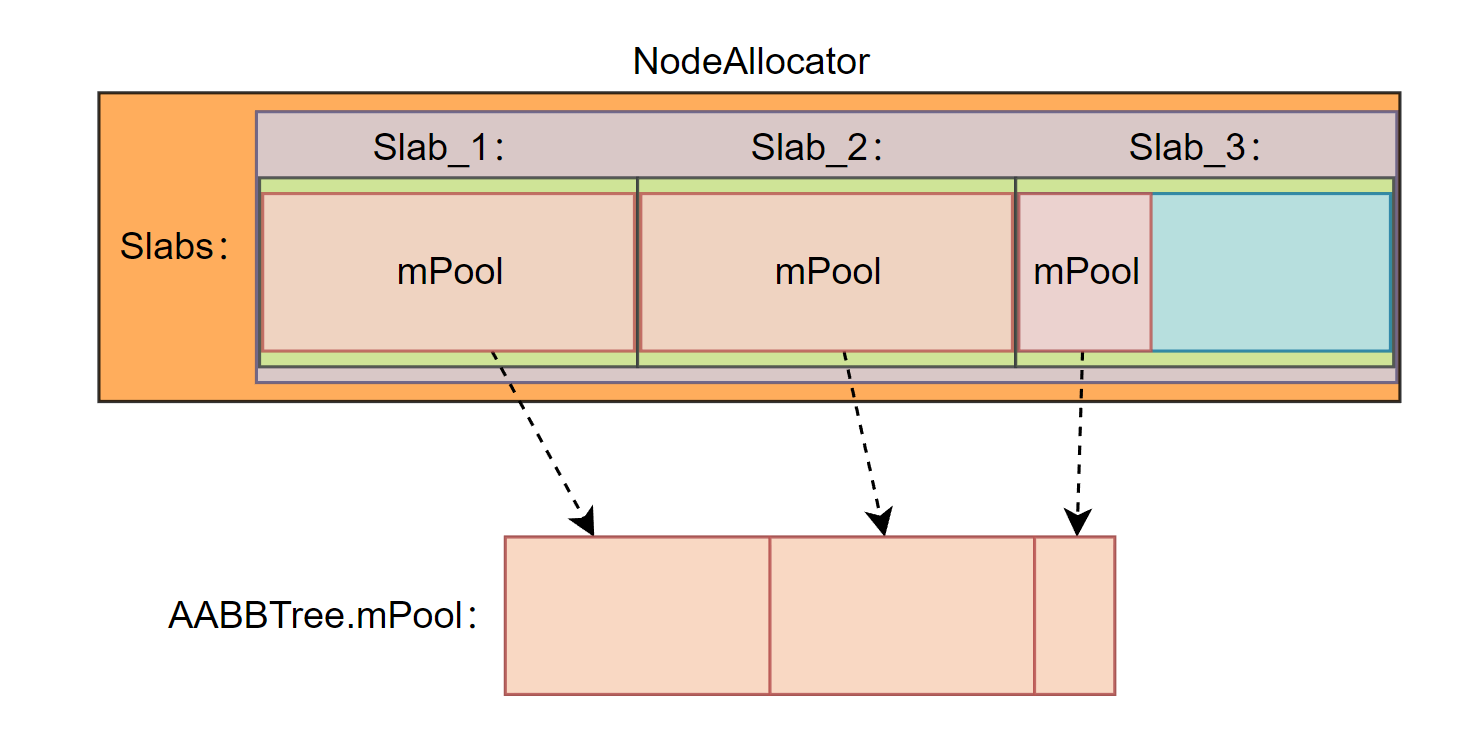
构建完成后，我们得到了一个构建时的 AABBTree，它由多个 AABBTreeBuildNode 组成。回想一下，所有的 AABBTreeBuildNode 实际上都通过 NodeAllocator 分配，并且存储在 Slab 的 mPool 中，而 NodeAllocator 对内存的使用远比我们想的要阔绰～
  • 由于 mPool 的分配机制决定了它也不那么的「节约」，其设计之初是为了解决零碎分配内存时多次调用 malloc 导致效率低下，以及单次大量分配内存导致卡帧的问题。因此第一次分配的时候会根据需要来预先分配最多 1024 个空闲节点，此后每次新创建一个 Slab，都会直接创建 1024 个新节点，可以想象其中不乏大量的空闲内存没有被利用，这样挥霍那还得了。
  • 另外 AABBTreeBuildNode 数量直接决定了整棵树的内存占用，如果不能缩减节点数量的情况下，压缩每个节点的数据大小也是一个不错的选择。
# flatten
为了高效利用内存，减少空闲内存的占比。把 NodeAllocator 内的 AABBTreeBuildNode 全部挪到一个定长的数组（AABBTree.mPool）中是个不错的选择。
当然这些都是基于一个前提： AABBTree 构建完成后，其节点应该是很少变更的。基于以上前提，引入了一个新的结构 AABBTree.mPool—— 一个 AABBTreeRuntimeNode 的数组。而 flatten 操作便是把 AABBTreeBuildNode 平铺到该数组中。
image-20220818092915969
除此以外，为了压缩 AABBTreeBuildNode 而引入的新类也有必要好好说道说道 ——AABBTreeRuntimeNode。
# AABBTreeRuntimeNode
相比于 AABBTreeBuildNode，做了更进一步的压缩，从原本的 40 字节压缩到了 28 字节：
image-20220817150220766
这个 mData 可谓是海纳百川，包罗万象。其存在两种解析规则：
  • 叶节点解析：叶节点解析规则中 U32 的前 27 位用来表示 AABBTree.mIndices 的下标也即是 mNodeIndex，后 4 位存储对象数量对应 mNbPrimitives，最后 1 位为 1 标识其为叶节点。
  • 非叶节点解析：非叶节点解析规则中 U32 的前 31 位用来记录它的左子树在 AABBTree.mPool 中的下标，最后 1 位为 0 标识其为非叶节点。
image-20220817151155864
# 全量分布构建（progressiveBuild）
聊完全量同步构建，接下来我们聊聊全量分布构建，这里的分布并非分开部署之义，而是分步骤构建。这样的构建模式可以让一帧内执行的构建操作转换为多帧执行，一定程度上解决了卡顿问题。下面就来看看其是如何实现的：
分布构建的实现本质上是把 AABBTreeBuildNode::_buildHierarchy 通过 AABBTree.mStack 先进先出队列转为非递归实现，再把非递归逻辑进行分批：
  • progress_0 ：初始化构建环境。
  • progress_1 ：把递归构建的左右子树，放入队列中。每次构建时从队列取出固定数量的节点进行分批构建。
    • 构建完毕后执行构建结果压缩。
PxU32 AABBTree::progressiveBuild(AABBTreeBuildParams& params, BuildStats& stats, PxU32 progress, PxU32 limit)
{
       if(progress==0)
       {
              if(!buildInit(params, stats))
                     return PX_INVALID_U32;
              mStack = PX_NEW(FIFOStack);
              mStack->push(mNodeAllocator.mPool);
              return progress++;
       }
       else if(progress==1)
       {
              PxU32 stackCount = mStack->getNbEntries();
              if(stackCount)
              {
                     PxU32 Total = 0;
                     const PxU32 Limit = limit;
                     while(Total<Limit)
                     {
                            AABBTreeBuildNode* Entry;
                            if(mStack->pop(Entry))
                                   Total += incrementalBuildHierarchy(*mStack, Entry, params, stats, mNodeAllocator, mIndices);
                            else
                                   break;
                     }
                     return progress;
              }
              buildEnd(params, stats);
              PX_DELETE_AND_RESET(mStack);
              return 0;      // Done!
       }
       return PX_INVALID_U32;
}
分布构建最大的意义在于削峰，这里暂时按下不表，后面针对 AABBPruner 的介绍再做展开
# AABBTree 的增删改
构建完成后 AABBTree 就已经可以支持场景查询的粗筛。然而要应对场景内物体的频繁移动、创建、销毁、变化，势必还得有一套能够兼容树变更的逻辑支持。
这里可以简单列举一下可能的场景：
  • AABBTree 的更新：物体移动了、且状态导致自生包围盒位置、大小、朝向发生变化，应该修改 AABBTree 中的包围盒信息。
  • AABBTree 的删除：物体销毁了，导致物体包围盒被销毁应该从 AABBTree 移除。
  • AABBTree 的新增：物体被创建，此时物体包围盒应该加入 AABBTree。
# AABBTree 的更新（mParentIndices && mRefitBitmask && mRefitHighestSetWord）
AABBTree 对于更新操作的实现，没有想象中的那么复杂。不会做节点的拼接，左旋右旋等复杂规则，而是简单的从下至上的依次更新每个包围盒的大小。
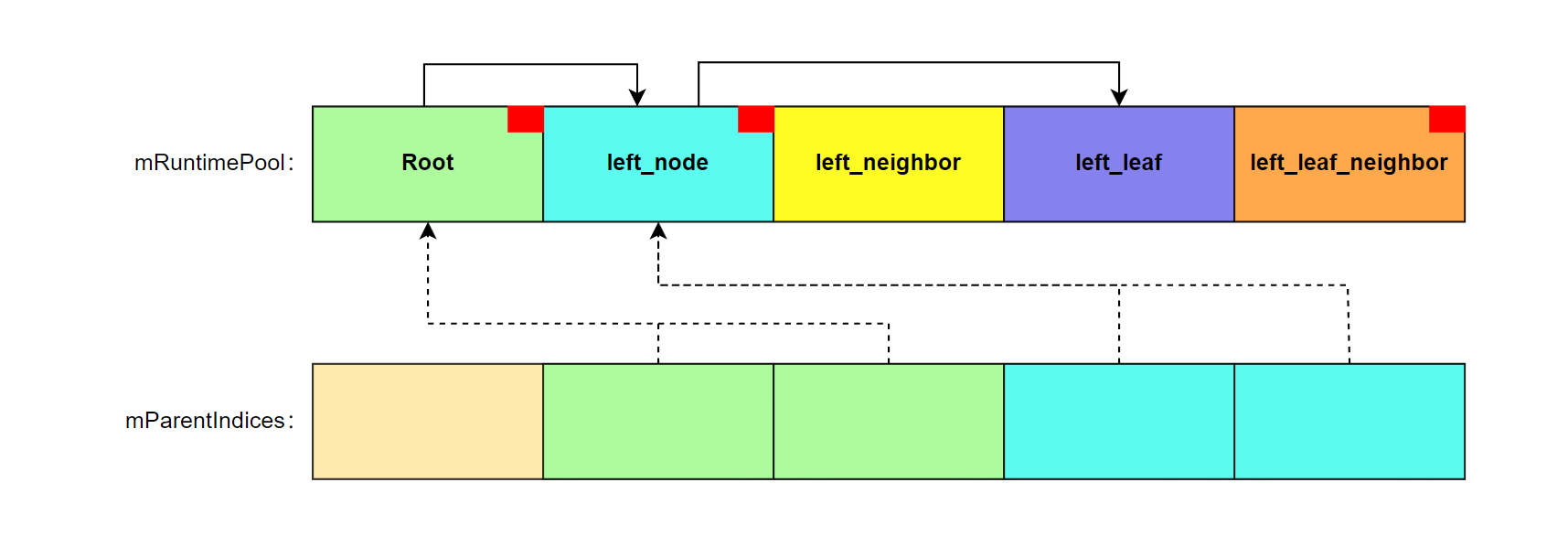
既然要实现从下至上的更新，势必需要知道每个子节点所对应的父节点是谁，因此用一个额外的数据结构进行存储 ——mParentIndices。
# mParentIndices
该结构也非常的简单，就是记录了每个子节点和父节点在 mRuntimePool 内的下标映射。
image-20220818163653380
# mRefitBitmask
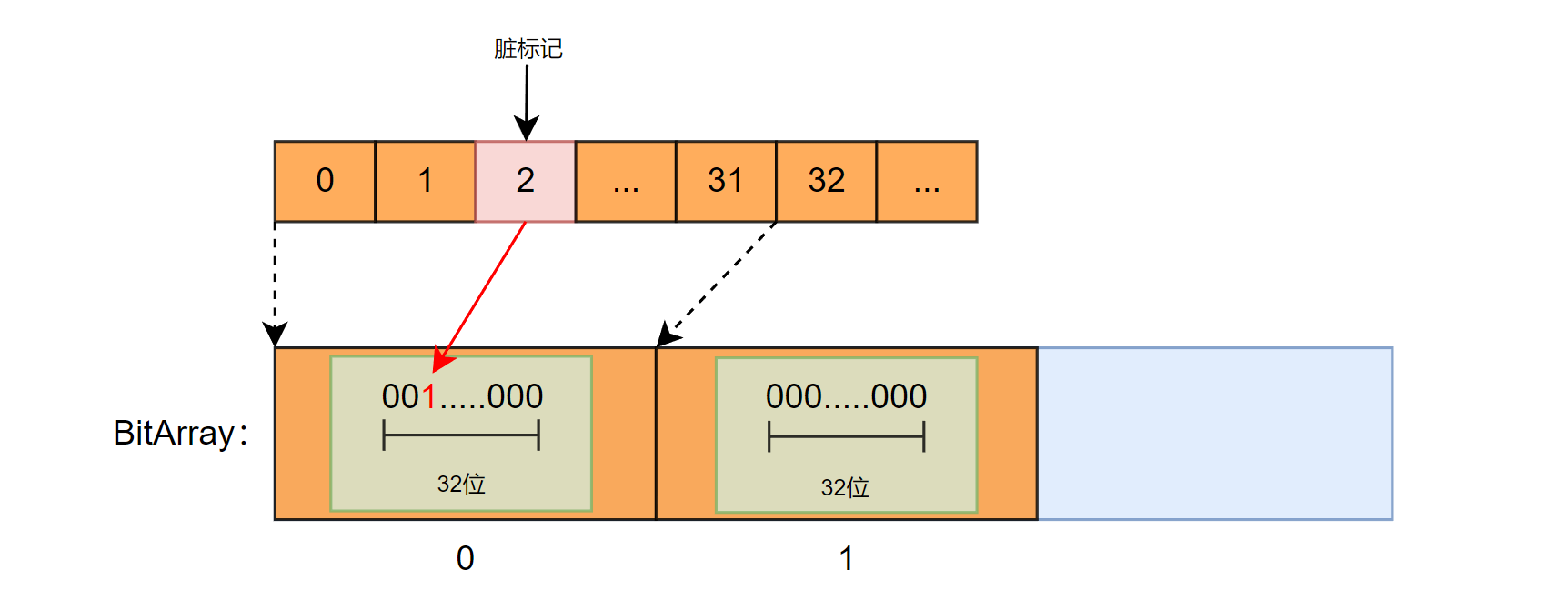
为了能快速定位需要更新的节点，这里对节点索引做了一个新的映射 ——mRefitBitmask。
该结构底层实现是一个 BitArray。对 U32 的节点编号进行分段存储，前 27 位作为 BitArray 的下标，后 5 位压缩到一个 U32 的每个 bit 内。通过如果某 bit 为 1，则表示对应编号（ BitArrayIdx << 5 + U32_bit_pos ）的节点需要被更新。
image-20220818113136693
# mRefitHighestSetWord
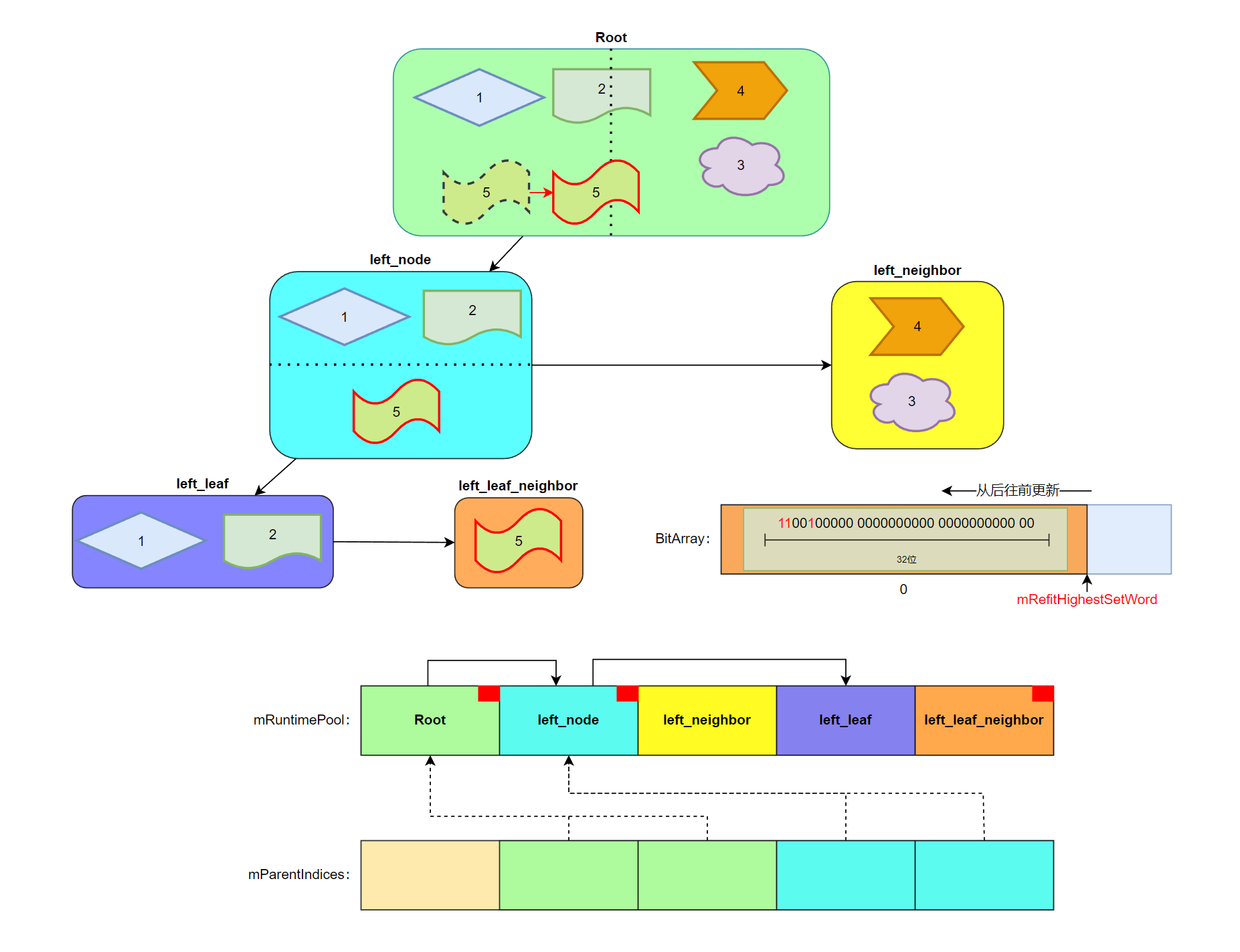
mRefitHighestSetWord 则是记录所有上标记脏节点里，BitArray 下标的最大值。因为更新的时候由于 AABBTree 构建顺序，父节点永远是排在子节点前面的，因此需要先更新子节点再更新父节点就必须从后往前的进行更新。
# 更新流程总结
如下图，假设 5 号图形发生了位移：
  • 那么其所在的包围盒 left_leaf_neighbor 会打上脏标记。
    • 根据 mParentIndices 依次标记器父节点 ——left_node、Root。
    • 体现在 BitArray 内，下标为 0 的 U32 中 1、2、5 位被打上了脏标记。
    • mRefitHighestSetWord 会被设置为 0，标识最大脏数据在 0 下标和其之前的位置。
  • 根据 mRefitHighestSetWord 从后往前更新所有带有脏标记的节点，并更新包围盒信息。
  • 最后清理所有的脏标记完成本次更新操作。
image-20220818163716796
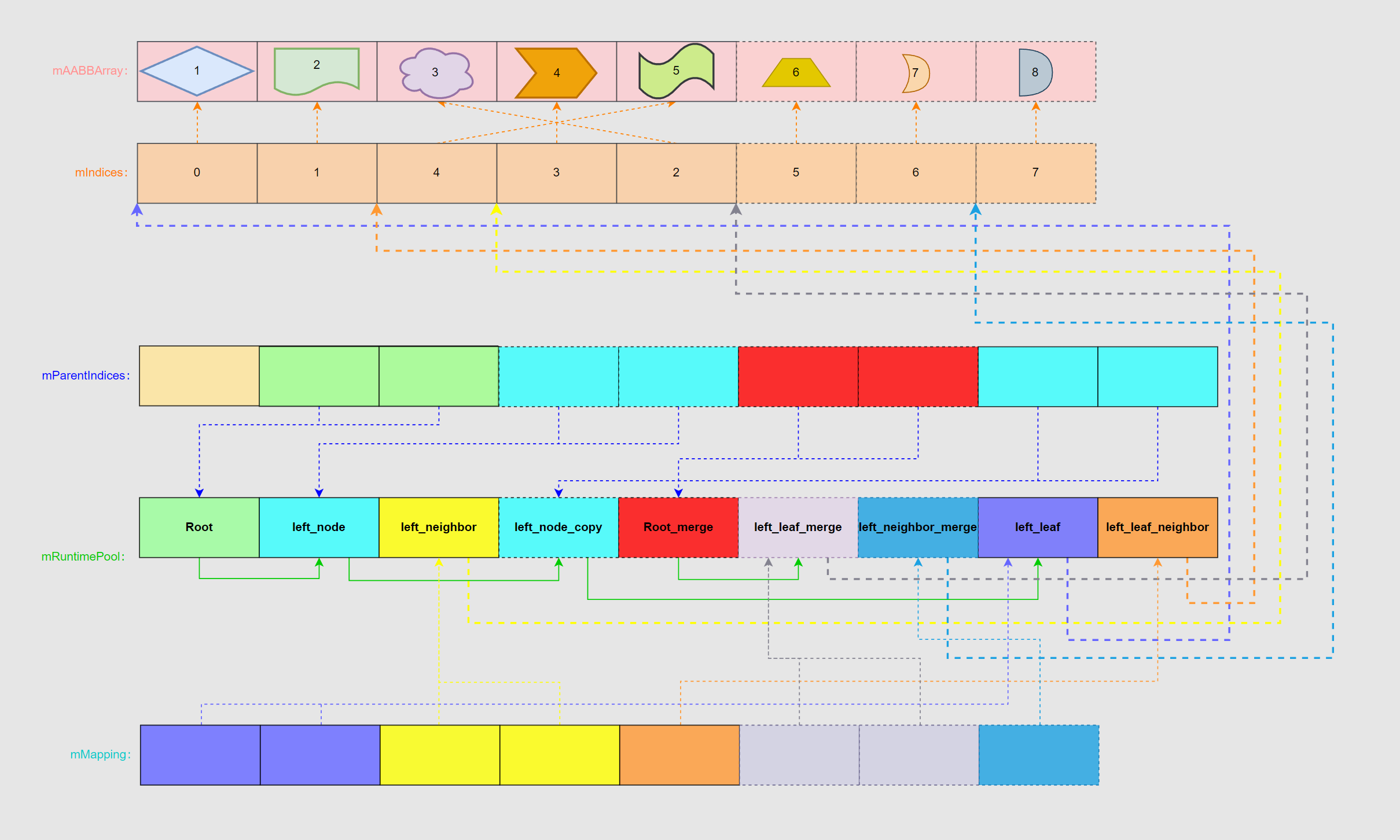
# 已知的映射关系总结
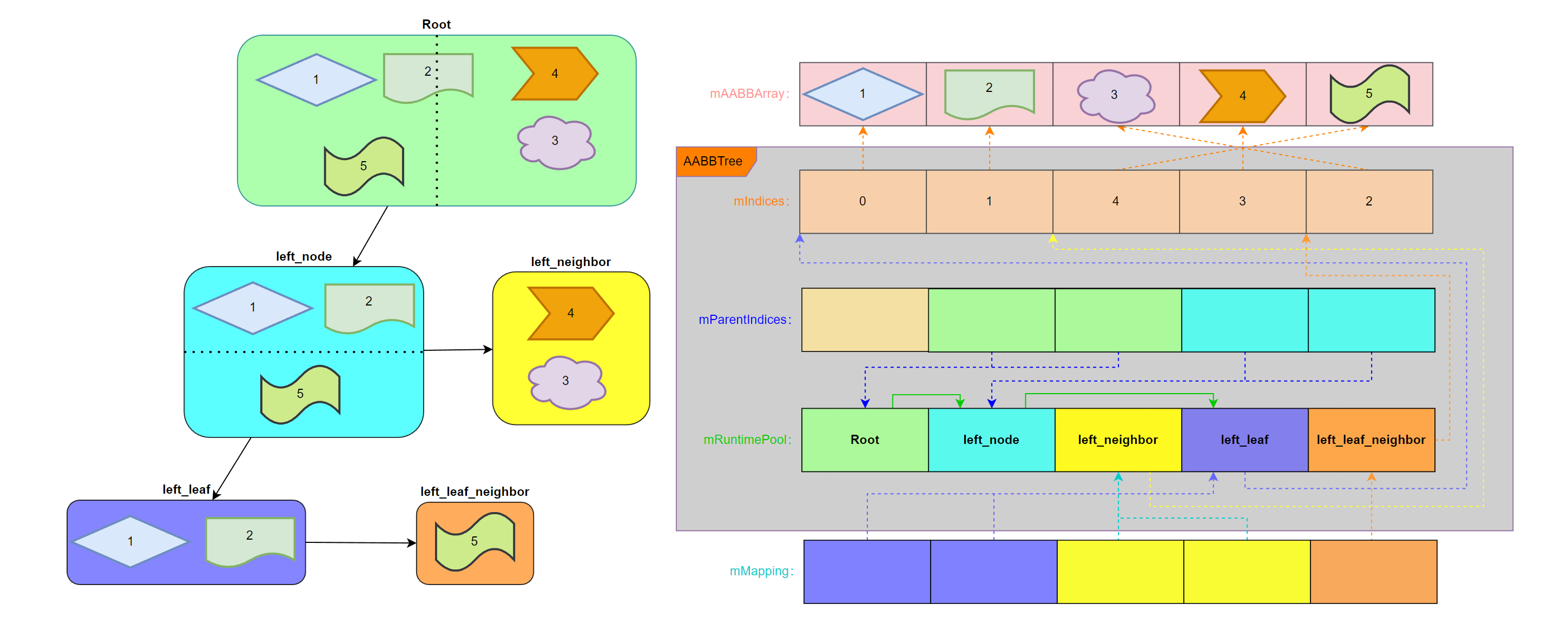
再介绍删除和新增之前，有必要系统性的梳理一下目前 AABBTree 内所用到各种映射、存储之间的关系。因为后续增删过程中同样少不了更新这些关系：
  • AABBTreeBuildParams.mAABBArray：外部包围盒数据，作为 AABBTree 构建的源数据，作为参数传递给 AABBTree。
  • AABBTree.mIndices：对 mAABBArray 做的二次映射，存储排序后的 mAABBArray 下标。
  • AABBTree.mRuntimePool：存储所有 AABBTree 节点运行时状态。
  • AABBTree.mParentIndices：维护 mRuntimePool 内部父子节点关系的映射。
  • AABBTreeUpdateMap.mMapping：维护 mAABBArray 到 mRuntimePool 的反向映射。
这里有关 AABBTreeUpdateMap 的话题，我们暂且先不讨论，只需要知道其它是一个外部的映射即可。
综上所述的五种存储内容，大致可以描绘出它们之间的关联关系：
image-20220818164030941
# AABBTree 的删除（AABBTreeUpdateMap::invalidate）
删除操作比较特殊，并不是在 AABBTree 内部完成的，原因也很简单：AABBTreeBuildParams.mAABBArray 并不属于 AABBTree 的数据，AABBTree 至始至终都只是维护了 mAABBArray 中的包围盒关联信息并缓存了包围盒数据。
所以删除的时候其实是删除 mAABBArray 数据，并且清理 AABBTree 内部关联的映射，这里以「图形 1」为例：
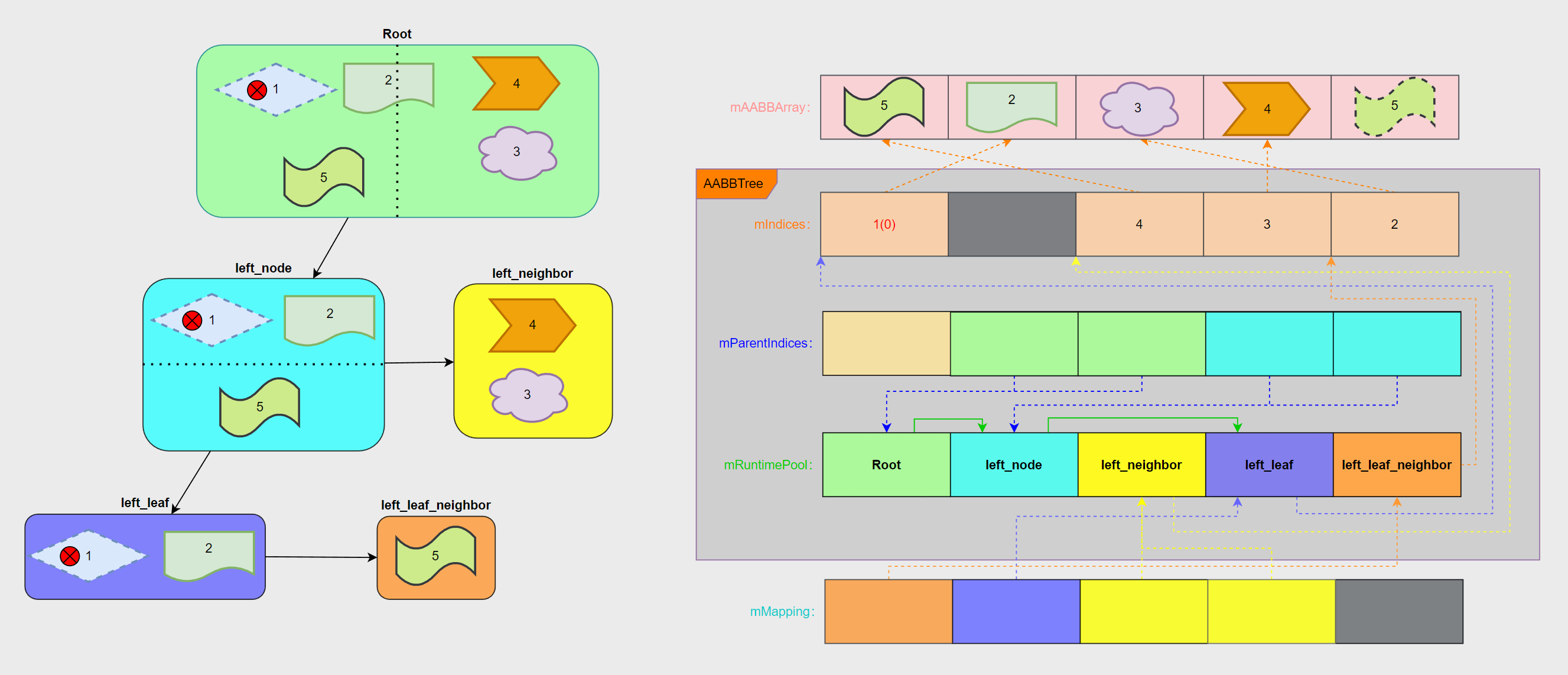
image-20220908110312390
  • 删除「图形 1」必然导致 mAABBArray 内部的包围盒数据被清理，为了保证包围盒数据的紧凑，会把最后一个图形 5 替换到图形 1 的位置。
  • mIndices 会移除掉对「图形 1」的索引；考虑到 mIndices 存储的每个节点下标必须是连续的，会对调所影响节点（left_leaf）的最后一个索引 mIndices [1] 到删除位置 mIndices [0]。
  • 由于图形 5 替换到图形 1 所在的位置，因此 mIndices [2] 也需要调整指向。
  • mMapping 同样需要进行调整，由于图形 1 替换为图形 5，因此 mMapping [0] 需要指向 left_leaf_neighbor
  • 最后，删除完毕同样需要进行一次更新操作。
这里有点需要注意：删除过后，内存并不会回收，因此如果大量创建对象再销毁，实际上分配给 AABBTree 的这部分内存还是会一直被占用。
# AABBTree 的新增（mergeTree）
新增操作同样比较特殊，AABBTree 并不会进行频繁的包围盒插入，然后再切分树节点，或者左旋右旋来调整树结构。而是采用了更加巧妙的手法：
由于 AABBTree 本身并不具备频繁插入的结构性质，因此采用：把多次新增操作视作新建一棵 AABBTree，然后和当前的 AABBTree 进行合并。
而合并的时候对需要合并的 AABBTree 做了数据上的裁剪，仅保留了构建所需的额外信息 ——AABBTreeMergeData。
# AABBTreeMergeData
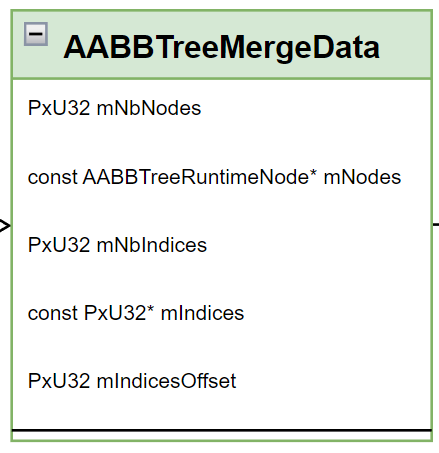
  • mNodes：就是构建好后的 AABBTreeRuntimeNode 列表，类似 AABBTree.mRuntimePool。
  • mIndices：就是对参与构建的包围盒做的排序后的列表，类似 AABBTree.mIndices。
  • mIndicesOffset：暂且不提。不过看这个命名想必大家也能猜出一二。
# AABBTree 合并
两棵树的合并可以视作把一棵树挂接到另一棵树的某个节点下面。至于如何判断应该挂接到哪个节点上，则是通过包围盒的包含关系决定。例如 merge_tree 根节点的包围盒被当前树的某个叶节点包含，那么直接插入到该叶节点下方；如果 merge_tree 根节点被某个非叶子节点包含则继续向下查询，直到遇到无法包含的情况下插入到其父节点；另外一种特殊情况则是当前树的根节点就已经不包含 merge_tree 了，则直接把 merge_tree 插入当前树的根节点。
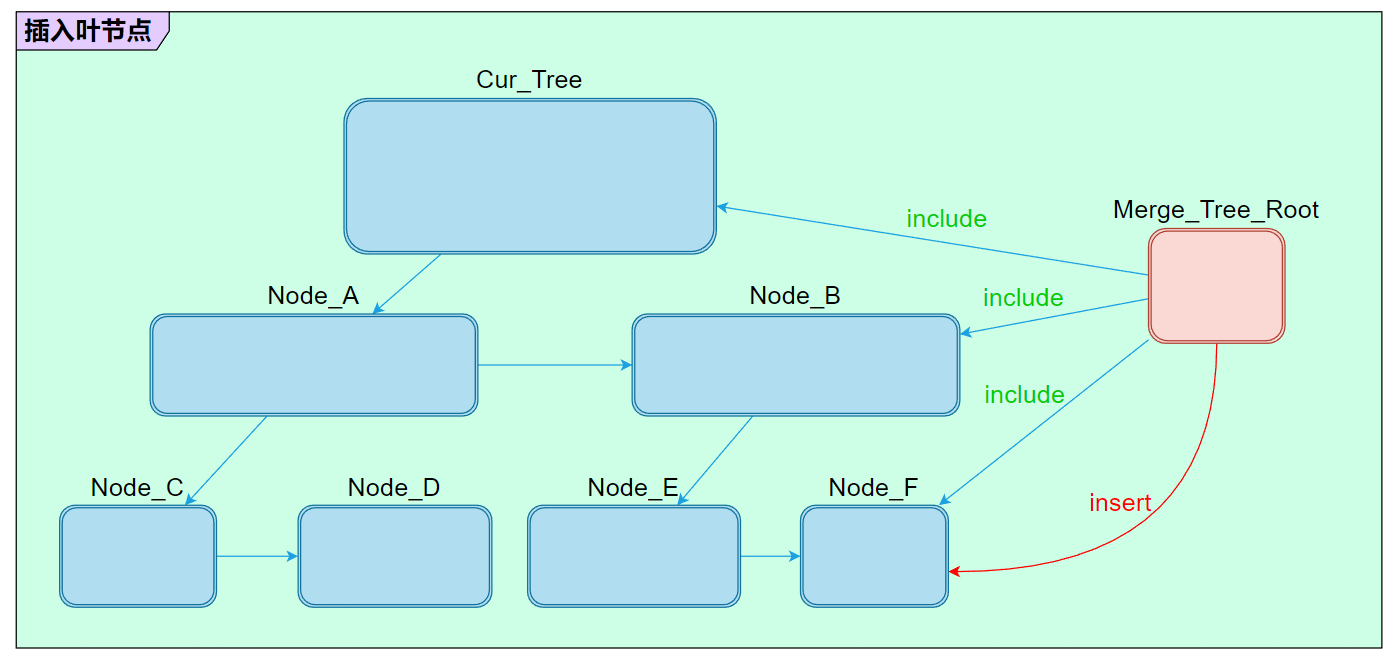
image-20220819105506653
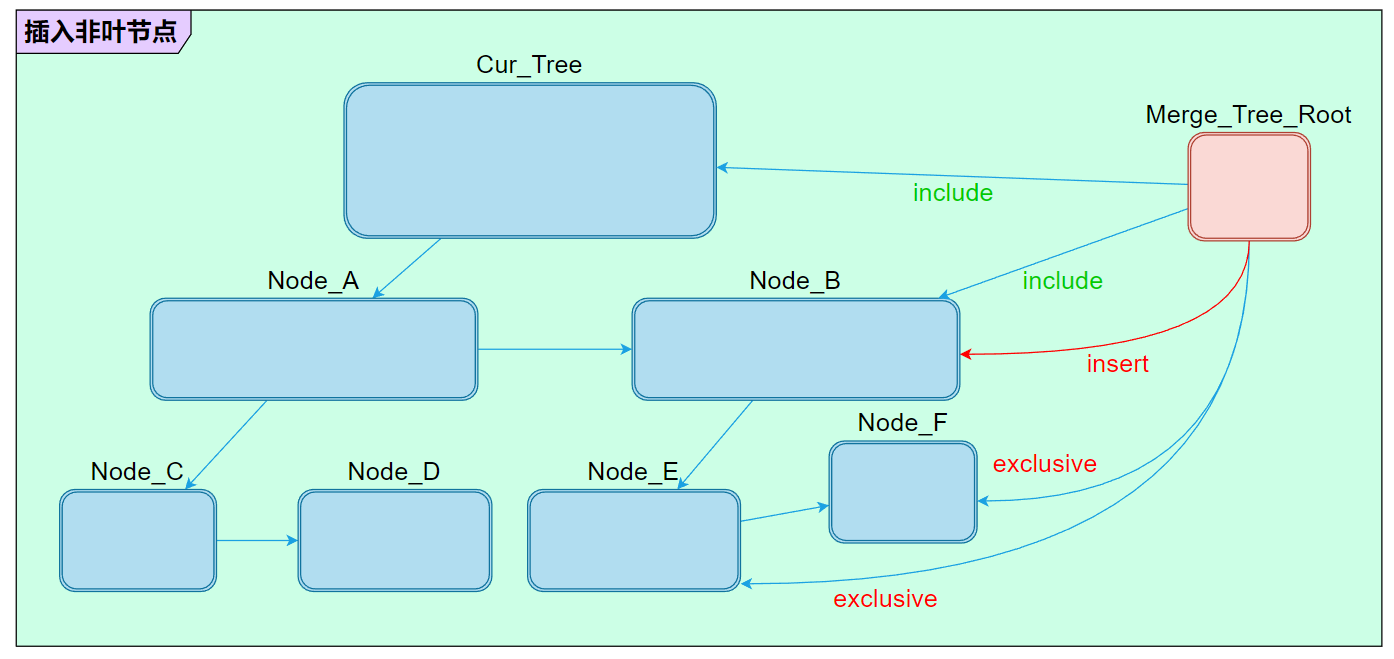
image-20220819105517413
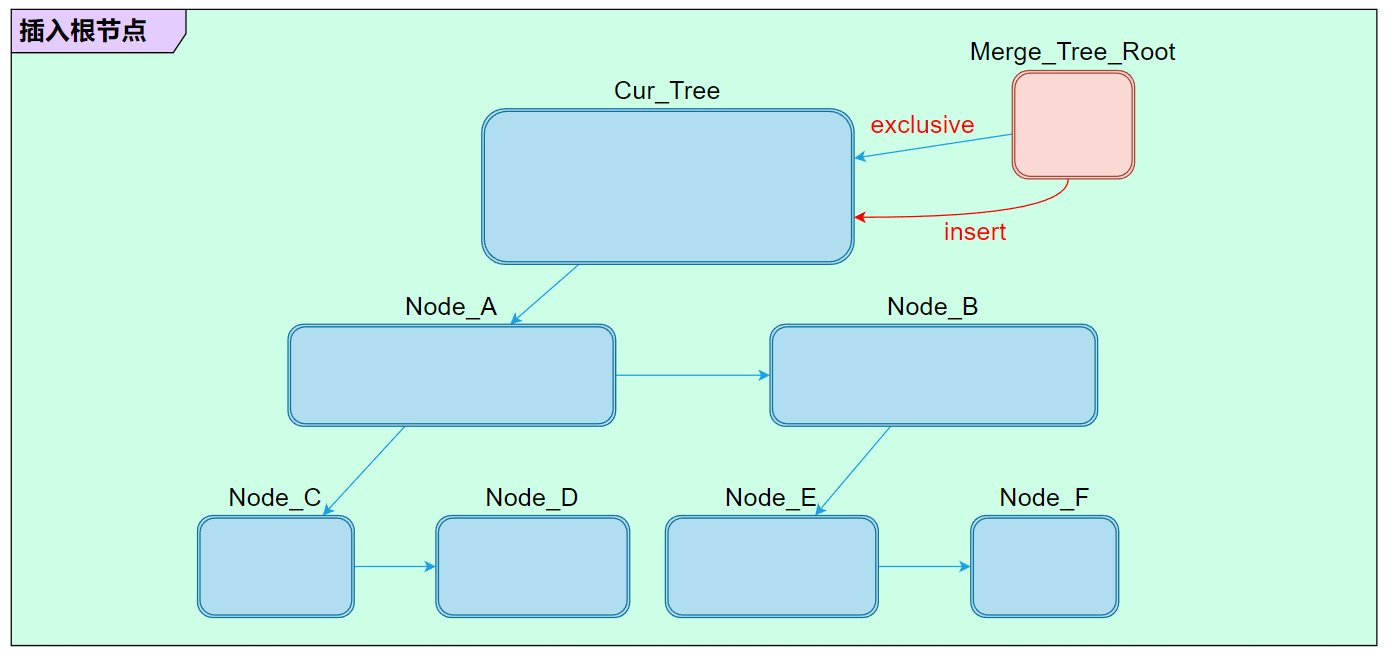
image-20220819105535856
综合以上三种情况，合并的逻辑大致可以分为两套：
  • Case_1：合并到某个叶节点。
  • Case_2：合并到某个非叶节点。
# 合并到叶节点
例如这里把 TreeB 合并到 TreeA 的「叶节点 left_neighbor」下面：
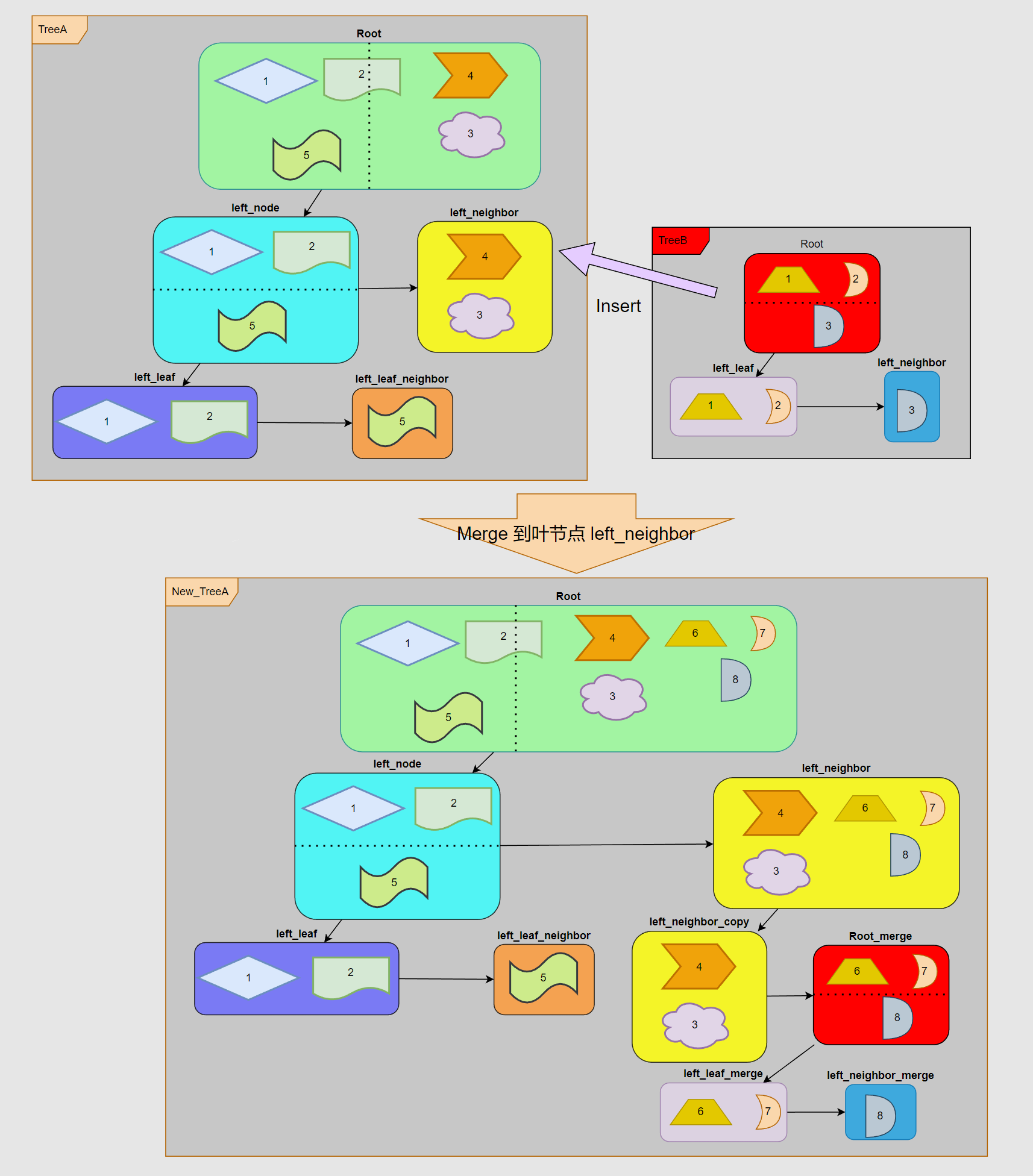
image-20220819111350287
叶节点的插入相对会比较的简单：
  • 首先会创建一个 left_neighbor 的拷贝 left_neighbor_copy，然后把 left_neighbor_copy 挂接在 left_neighbor 的左子树下面，这时候 left_neighbor 会从一个叶节点变更为非叶节点，最直观的体现是 AABBTreeRuntimeNode 的 mData 会进行调整。
  • 接着把 TreeB 的 Root 拼接到 left_neighbor 右子树节点。整个过程大体就算告一段落。
  • 最后更新一下所有节点的关联关系，整个合并流程就算结束了。
# 合并到叶节点的数据变更
合并到叶节点的插入相对也较为简单，会在原有数组的基础上向后插入新的节点数据，并且把涉及到的相关节点进行调整。
  • 由于 left_neighbor 从叶节点变为非叶节点，因此需要修改 AABBTreeRuntimeNode.mData 让其能够指向 left_neighbor_copy。
  • 新加入节点都需要重新构建 mMapping、mRuntimePool、mParentIndices、mIndices、mAABBArray 关系网，其他不受影响的节点则不需要进行调整。
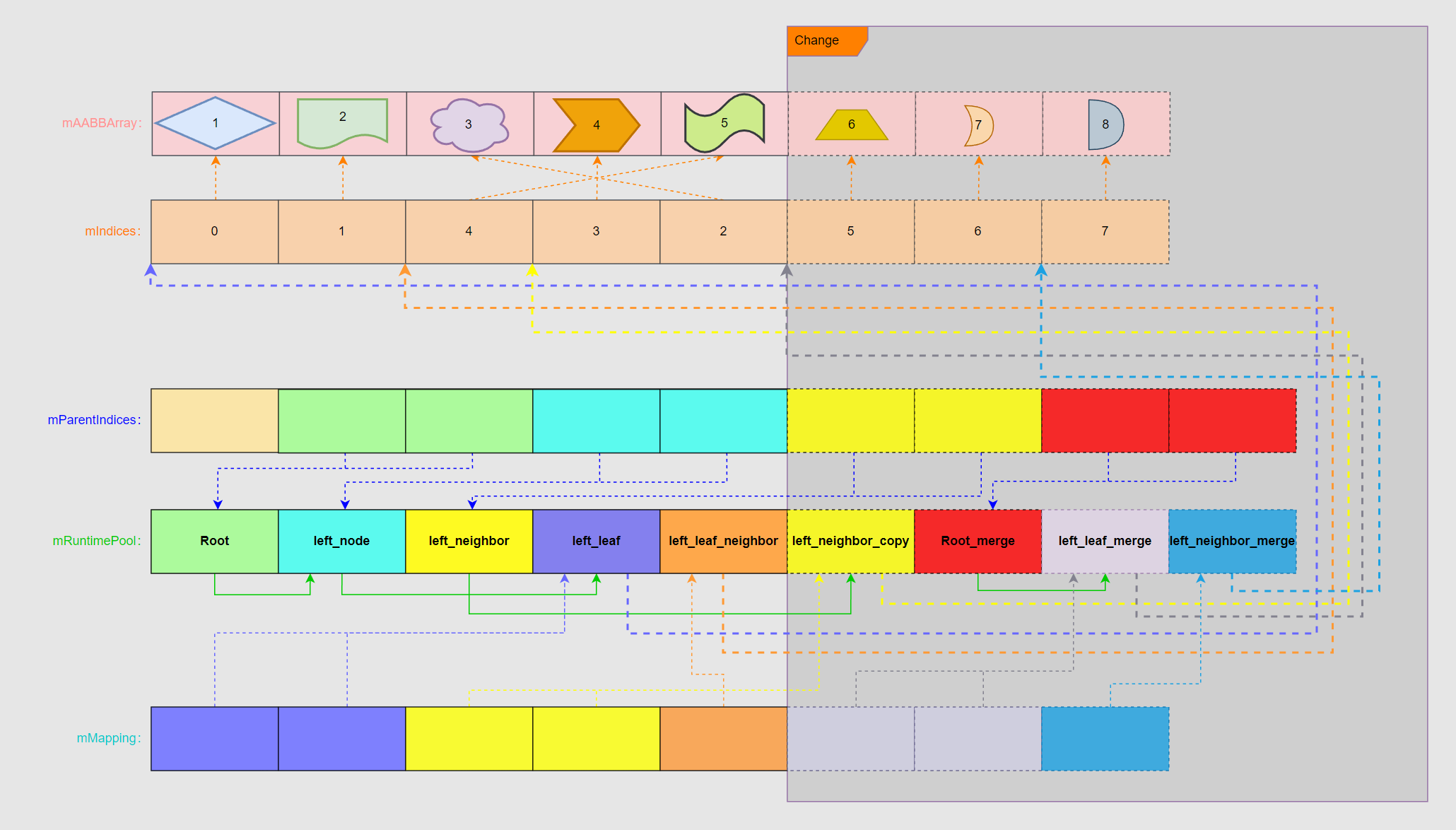
image-20220819120317839
之前也提到，mRuntimePool 本身是定长的，因此每做一次 merge 操作就需要 resize 一次数组，并且做一次全拷贝，开销还是比较高的。
# 合并到非叶节点
合并非叶节点和合并叶节点非常的近似，都是拷贝一份插入节点并把 merge_tree 作为左子树进行拼接：
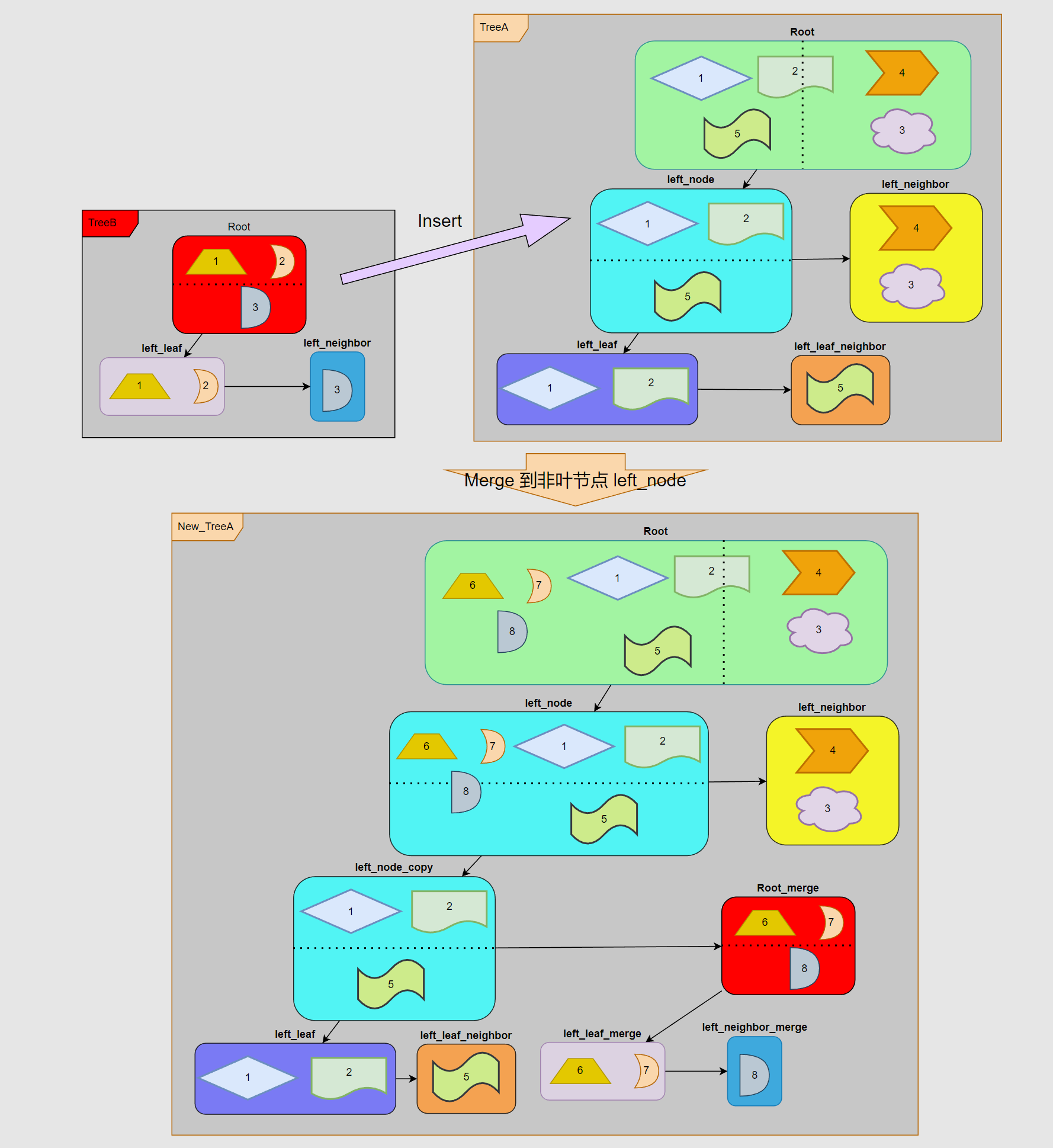
image-20220819113416849
  • 首先会创建一个 left_node 的拷贝 left_node_copy，然后把 left_node_copy 挂接在 left_neighbor 的左子树下面，并把 left_node 子节点转移到 left_node_copy 下面。
  • 接着把 TreeB 的 Root 拼接到 left_node 右子树节点，和 left_node_copy 相邻。整个过程大体就算告一段落。
  • 最后更新一下所有节点的关联关系，整个合并流程就算结束了。
# 合并到非叶节点的数据变更
可以看到，新增的 Root_merge 等内容插到了 mRuntimePool 的中间位置。原因也很简单，如果和插入叶节点一样放在 mRuntimePool 末尾的话，会导致 left_leaf 和 left_leaf_neighbor 会在 Root_merge 之前，这样显然是不满足父节点和父节点兄弟节点必须在子节点之前的特性，这样会导致 AABBTree 从下而上（从后往前）的层级更新发生异常。
因此这里选择把整棵 merge_tree 插入到了非叶节点的左子树（原 left_leaf 处）。而代价则是需要重新设置受影响的节点 ——left_leaf 和 left_leaf_neighbor。
image-20220819150406006
# 总结
到此，AABBTree 的组成、构建和更新都介绍完毕～，但这还远没有结束。我们一直没有提到的 AABBTreeUpdateMap，以及从何而来的 AABBTreeBuildParams 都还值得继续探讨；另外，AABBTree 的分布构建下的削峰策略也还没有实质上的体现。