首页 学习 Games系列 GAME202高质量实时渲染

以下为个人学习笔记整理，课程官网传送门，作业传送门，会议系统传送门。

# Real-time Ray Tracing（RTRT）

# what does RTX really do？

「RTX」硬件的设计主要是用于加速光线和场景求交速度。—— 每秒 100 亿根光线。

# 1 SPP path tracing：

最基本的 sample per pixel（SPP）：

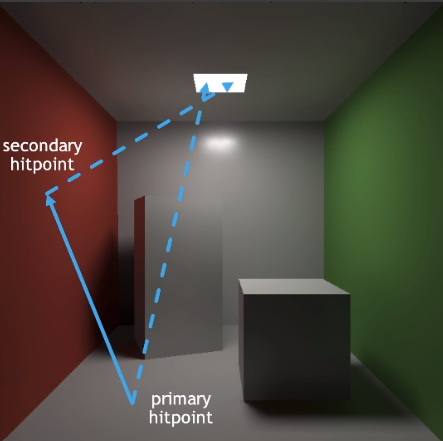
  • primary hitpoint：从摄像机观察到的像素点（shading point）
    • 1 rasterization（primary）：从摄像机到「shading point」的光线。
    • 1 ray（primary visibility）：从「shading point」到光源的光线 —— 用于计算是否可见。
  • secondary hitpoint：周围的能对「shading point」有贡献的点「间接光源」
    • 1 ray（secondary bounce）：由「shading point」经过一次反射到「间接光源」的光线。
    • 1 ray（secondary visibility）：从「间接光源」到光源的光线 —— 用于计算是否可见。

image-20210622100839877

SPP 数量太少会导致画面有噪点，因此 ray tracing 的核心在于 Denoising

image-20210622101935798

降噪操作前后的对比：

image-20210622110600950

# Denoising Goals

  • Quality：
    • no overblur
    • no artifacts
    • keep all details
  • Speed：每帧的耗时不能超过 2ms。

# Key idea

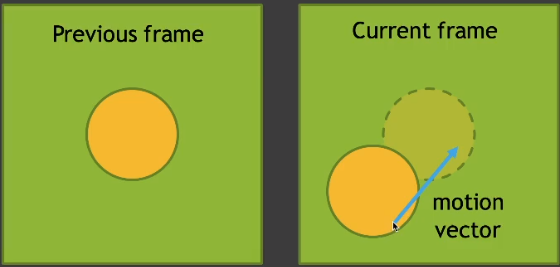
  • 假设每一帧的前一帧已经做了「Denoising」。
  • 假设每个物体的运动都是连续的，可以使用「motion vectors」去获取以前的位置。然后就能用之前某点已经「Denoising」后的结果用于当前帧。相当于增加了 SPP。

image-20210622113623723

# The G-Buffers

Geometry buffer：

  • screen space info：仅仅只是记录屏幕空间的信息。
  • during rendering is free：渲染过程中基本无性能开销，由于处理光线追踪过程中顺带就会计算，因此缓存结果以备后续使用不会影响性能。

image-20210622114006055

# Back Projection

给定一个像素，求出上一帧该像素的信息：

  • 如果「G-buffer」有缓存世界坐标的信息，那么可以直接去拿。
  • 或者计算：s=M−1V−1P−1E−1xs = M^{-1} V^{-1} P^{-1} E^{-1}x。输入的 xx 是一个 3D 的向量。逆向求出像素对应位置在物体在空间中的坐标
  • Motion is known：$s^\prime} \xrightarrow{T} s, s({\prime)= T^{-1}s $
    • 由于物体运动已知，因此可以预测物体下一帧移动到的位置。
    • 得到了世界坐标移动后的位置，在进行 x′=E′P′V′M′s′x^{\prime} = E^{\prime}P^{\prime}V^{\prime}M^{\prime}s^{\prime} 变换到屏幕坐标。

image-20210622143715551

# Temporal Accum./Denoising

# some denote:

  • 「~」：unfiltered，还没做过「filtering」。
  • 「-」：filtered，已经做过「filtering」。
  • 无：表示已经累计过一些结果。

# This frame（i-th frame）

先对当前帧做个 filter 降噪。

Cˉ(i)=Filter[C~(i)]\bar{C}^{(i)} = Filter[\tilde{C}^{(i)}]

再和上一帧做一个「linear blend」， $ \alpha : 0.1 \sim 0.2$ 。

Cˉ(i)=αCˉ(i)+(1−α)Cˉ(i−1)\bar{C}^{(i)} = \alpha \bar{C}^{(i)} + (1 - \alpha)\bar{C}^{(i - 1)}

# Temporal Failure

  • 【case1】基于时间复用的渲染，需要一定时间的预热（burn-in period）才能达到比较好的效果。

    • 场景切换了 or 第一帧如何处理。
    • 不同帧之间的光源变换剧烈。
    • 不同镜头的频繁切换。

  • 【case2】由于会复用上一帧结果，倒退行走（很多新的画面会加入屏幕空间），这部分内容也会缺乏预热。

  • 【case3】由于遮挡物移动，导致不断出现的新物体（disocclusion）。

image-20210622152654356

如果不解决这些问题，依旧还是用上一帧结果和当前帧进行「linear blend」，将会出现拖尾效果。

image-20210622153156890

# Adjustments to Temp. Failure

# Clamping

试图拉近上一帧和当前帧值之间的差距，可以取上一帧某个像素点周围区域做个平均等。

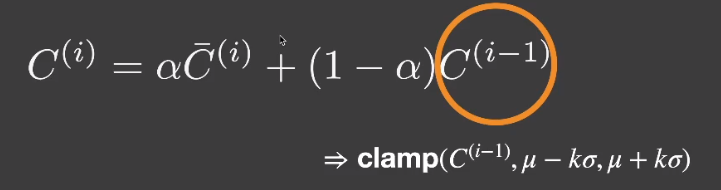
image-20210623153412651

# Detection
  • 检查像素点的上下两帧物体是否一致。
  • 在上一帧不太可信的情况下，适当调整 α\alpha 的值，从而控制以下上一帧贡献度占比。
  • 换用更加强大的滤波器（filter）。

但是这样做依然会再次引入噪点。

# More Temporal Failure

加入在一个场景内，任何物体都没有移动，只移动光源的情况下，那么每一帧的「motion vector」都是 0 ，这样显然是会存在问题的，因为光源移动，必定会影响阴影的位置。

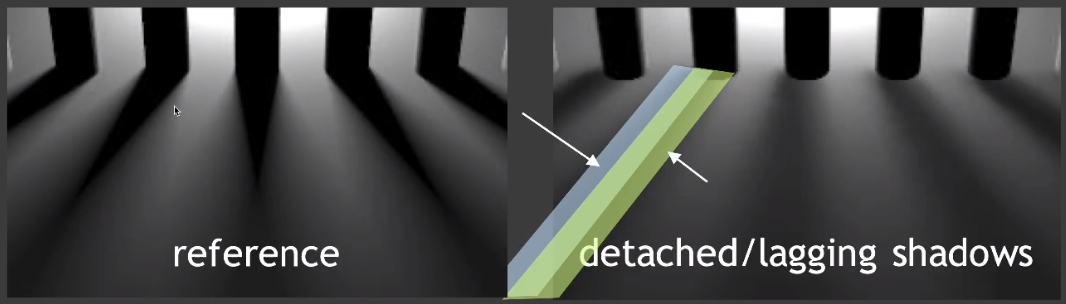
image-20210622154619273

另外对于「glossy」的物体，其反射的其他周围物体如果移动，理论上，反射内容也会发生变化，但是「glossy」物体本身没有移动，因此看上去反射结果将会有一定程度上的滞后。

image-20210622155003490

# Implementation of filtering

需要对图像进行（low-pass）低通滤波的处理。

  • 去掉高频信息，保留低频信息。
  • 只处理屏幕空间内的信息。

image-20210623084920192

  • Inputs

    • A noisy image \tilde
    • A filter kernel KK

  • Output

    • A filtered image \bar

通常情况下进行滤波会采用近似「Gaussion」分布的滤波核

  • 范围内的任意一点都会对结果产生贡献。
  • 任意点的贡献度取决于和结果的距离。

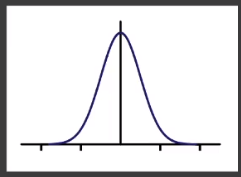
image-20210623085542793

# Bilateral filtering

「Gaussion filtering」会让画面变得模糊。但往往有时，人们希望保留图像清晰的边界。

image-20210623090827549

「Bilateral filtering」目的是为了能够保留图像边界的同时，对其他部分进行「filtering」。

  • 判断任意点对结果的贡献时，需要先判断两点之间的颜色差是否足够小。如果过大的话说明处在边界位置，这时候就不应该对结果产生过多的贡献。

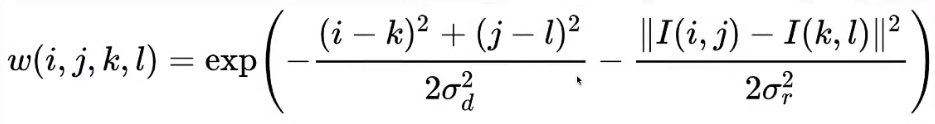
image-20210623092225400

(i,j)(i,j) 和 (k,l)(k,l) 分别表示任意点和结果点。

得到的结果看上去边界就会比较的清晰。但是这种情况下很难区分噪声和边界，导致一些噪声残留。

image-20210623092445981

# Joint Bilateral Filtering

  • 「Gaussian filtering」：1 metric（distance）
  • 「Bilateral Filtering」：2 metric（distance & color difference）
  • 「Joint Bilateral Filtering」：use more metric

由于渲染过程中能够获取到屏幕空间内各个像素的各种信息：坐标、法线、反射率... 因此，可以考虑把它们利用起来：

  • G-buffer 本身没有任何的噪声，因此可以确保得到的数值是准确的。

image-20210623093225086

# Note

  • Gaussion is not the only choice

image-20210623100605420

# Example

假设我们考虑以下因素

  • Depth：两点的深度相差太多的情况下，可以适当减少贡献度（A & B）。
  • Normal：法线方向相差太多的情况下，可以适当减少贡献度（B & C）。
  • Color：颜色相差太多的情况下，可以适当减少贡献度（D & E）。

image-20210623101246675

# Implementing Large Filters

大范围的「filtering」势必会造成性能开销的急剧上涨。常见的解决办法：

  • Separate Passes

# Separate Passes

针对 2D 的「Gaussion filtering」都拆分为对两个 1D 的「Gaussion filtering」，因此时间复杂度可以从 O(n2)→2O(n)O(n^2) \to 2O(n)

image-20210623114003518

# Why 2D 「Gaussion filtering」to two 1D 「Gaussion filtering」?

  • 高斯函数在 2D 下的定义本质上就是 1D 的拆分。

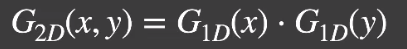
image-20210623114341511

  • filtering == convolution：滤波本质上就是做卷积。

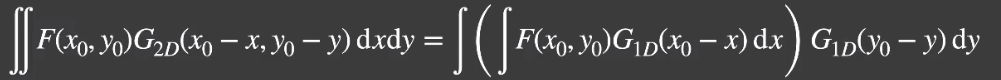
image-20210623114528835

「Gaussion filtering」能够拆分取决于高斯函数本身的性质，因此如果换成「Bilateral Filtering」或者其他滤波不一定适用。

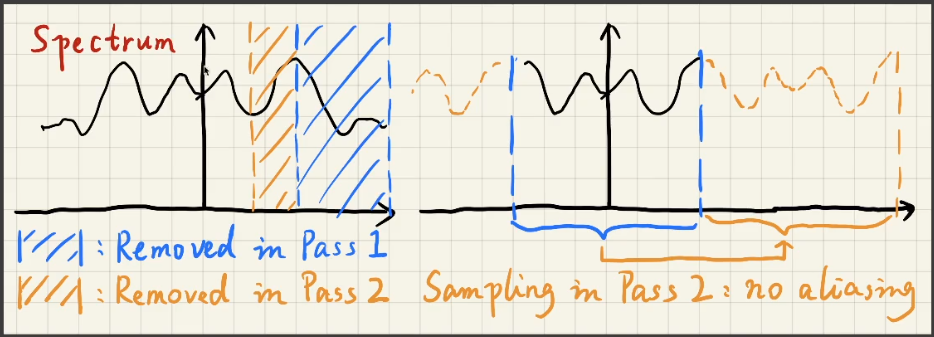
# Progressively Growing Sizes

不断扩大「filtering」大小进行滤波 ——「a-trous wavelet」

  • 每次都用一个大小的滤波进行「filtering」。例如： 5X5
  • 下次再用上次的结果再进行「filtering」，采用时每次的间隔不同。
  • $64 \times 64 \to 5 \times 5 $ 执行 5 次。

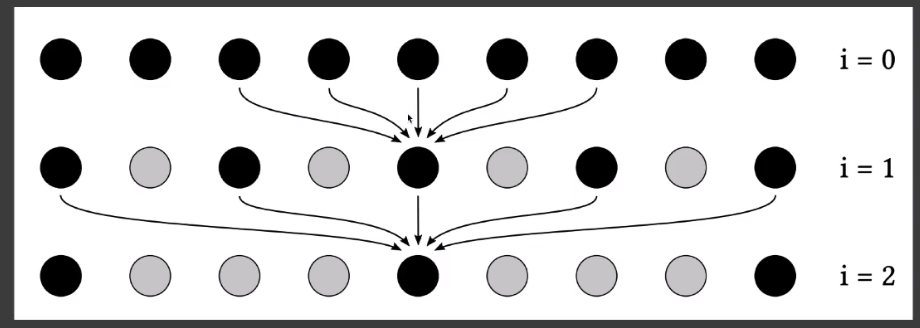
image-20210623141509062

# A deeper understanding

GAME101 频谱相关介绍

  • why growing sizes？
    • larger filter == removing lower frequencies：越大的「filtering」越是能够过滤掉更低的频率
  • why is it safe to skip samples？
    • Sampling == repeating the spectrum：采样间隔越大，频域之间的步长就越小，走样问题就是由于步长太小导致频谱的堆叠造成，但是由于之前已经做了一次低通滤波，假设滤波之后没有高频的信息了，那么小步长所造成的堆叠部分其实相当于已经提前被过滤掉了，因此不会有混叠问题，有点类似「反走样」的操作。

image-20210623142339550

# Outlier Removal

  • Filtering is not almighty
    • 对于一些非常亮的点（outliers），进行「filtering」只会让一个亮点变成一块更大的区域。

image-20210623151706964

因此需要在执行「filtering」之前，清除掉这些「outlier」

Outlier Removal 会让最后得到的画面能量丢失

# Outlier Detection and Clamping

  • 计算任意像素周围若干点的「均值」和「方差」。
  • 如果某个点的值超出了「均值」±「方差」* n，那么就可以视作「outlier」。
  • 需要对「outlier」进行「Clamp」操作挤压到可用范围内。

整体思路有点类似 [Temporal Clamping](#Adjustments to Temp. Failure)。

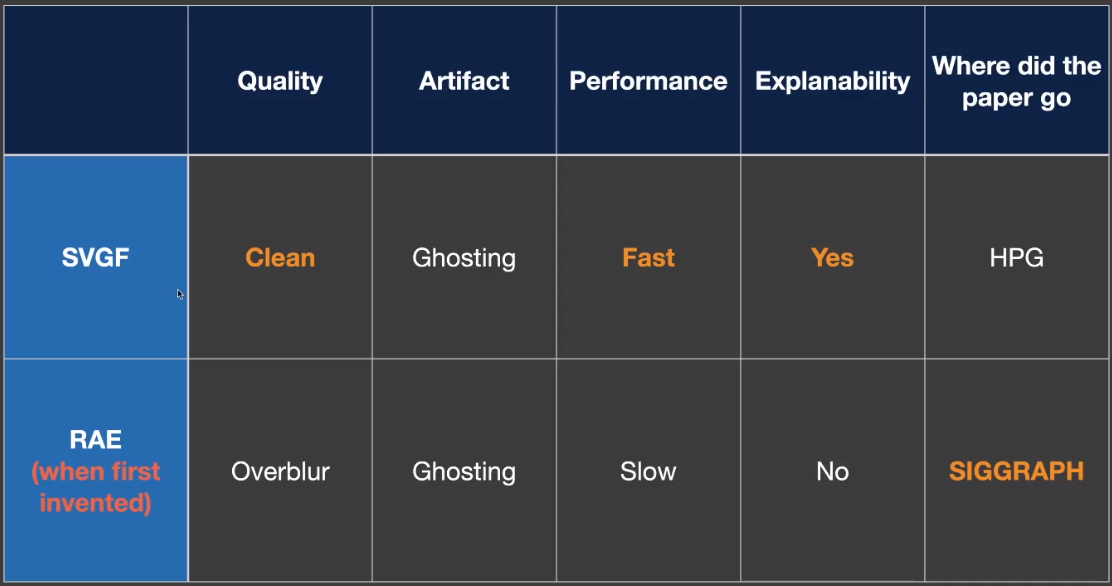
# Spatiotemporal Variance-Guided Filtering（SVGF）

# SVGF —— Basic Idea

  • 和「Temporal Denoising」很类似
  • 额外加入了每个像素点颜色的方差和

image-20210624105935928

# SVGF —— Join Bilateral Filtering

除了「distance」和「color difference」之外，又引入了三个 metric。

  • Depth
  • Normal
  • Luminance

# Depth

计算以点「p」沿着法线垂直方向的「法线梯度（斜率）」和「q」的距离去预测点「q」的可能深度。再和点「q」的实际深度进行比对，根据误差大小确定贡献度。

  • 如果两点在一个平面上，那么预测结果将会非常接近实际结果。
  • 如果不在一个平面上，那么大概率不在一个平面，这时候就可以适当减少贡献度。

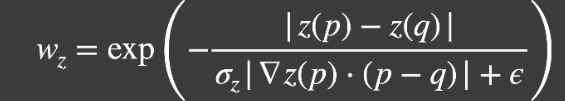
image-20210624110419558

image-20210624111421697

# Normal

两点的法线方向不同的话，可以近似认为两点不在一个平面，那么贡献度可以适当减少。

  • 一般情况下会在没有法线贴图的片段上进行计算，减少法线贴图的干扰。

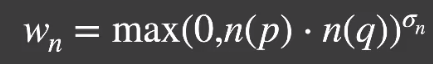
image-20210624111510906

image-20210624111529111

# Luminance

由于噪声「C」本身非常亮，虽然「color difference」能够区分点「A」和点「B」。但是没办法区分点「B」和点「C」，这会使得过亮的噪声「C」对于点「B」的贡献度很高，这时候就需要通过两点的亮度来进行进一步筛选。

  • 亮度筛选用的是点「B」颜色的方差和「B」、「C」两点颜色差的比值作为贡献度。
    • 方差的计算可以取周围 7X7 的点进行计算。
    • 再用「motion vectors」计算上一帧和当前帧的平均。
    • 再对当前帧的「B」点周围 3X3 的方差做个「filtering」。

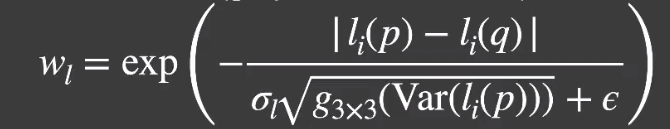
image-20210624111904378

image-20210624111915107

# SVGF —— Failure Cases

由于计算过程类似「Temporal Denoising」，因此也会存在拖尾现象。

image-20210624113850727

# Recurrent AutoEncoder（RAE）

# RAE —— Basic Idea

  • 基于神经网络的方法，对存在噪点的图进行「filtering」降噪。
    • AutoEncoder（or U-Net）神经网络结构。
  • 会使用到 G-buffers 的一些额外信息。
  • 存在一定的「Temporal」（复用之前的结果）。
    • Recurrent convolutional block：神经网络每层的输出可能会成为下层的输入，也可能成为上层的输入。

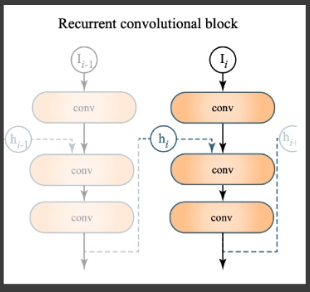
image-20210624114823560

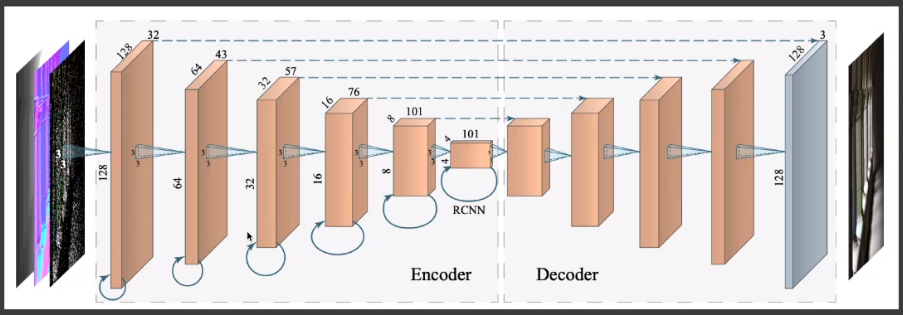
image-20210624114743608

# RAE —— Results

image-20210624115044800

# Comparison 「SVGF」VS「RAE」

image-20210624115312943