以下为个人学习笔记整理,课程官网传送门,作业传送门,会议系统传送门。
# Real-time Physically-based Materials
- Microfacet BRDF
- Disney principled BRDF
# PBR and PBR Materials
Physically-Based Rendering(PBR):基于物理的渲染。虽然不仅仅指代材质但通常情况下用于描述材质。
# PBR materials in RTR
「PBR」的材质要满足实时渲染的效率需求,因此种类相比于离线渲染较少。且为了效率,通常情况下并非基于物理的渲染。
# For surfaces
针对物体表目的渲染有以下两种:
- microfacet models:基于微表面模型的材质,并非「PBR」的
- Disney principled BRDFs:针对艺术家操作方便的「BRDF」,也不是「PBR」的

# For volumes
对于考虑体积的渲染(云、雾、毛发),为了效率通常考虑单光线多次散射结果,参考 GAME101 毛发渲染。
# Microfacet BRDF
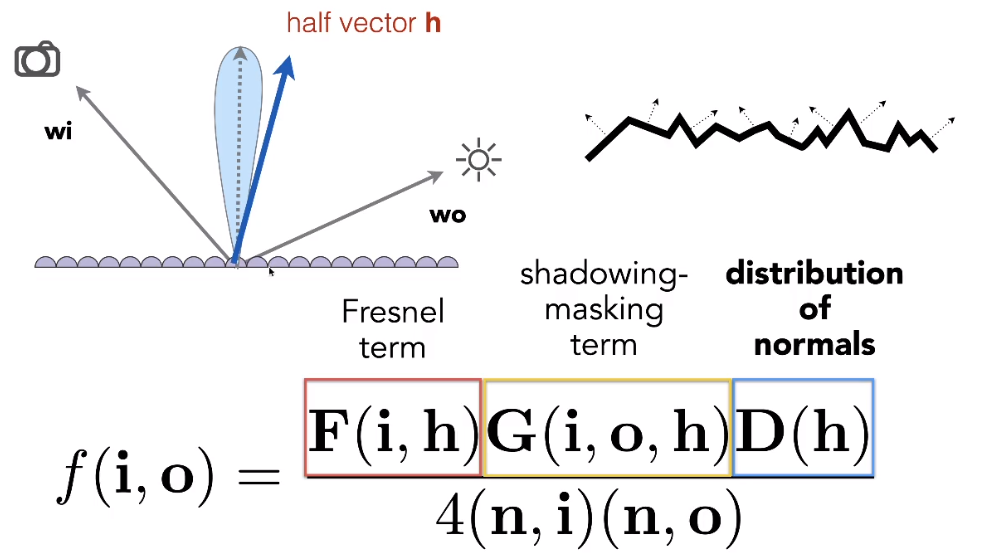
# Fersnel Term——Formulae
描述入射光经过物体表面后能够被反射出的光线。
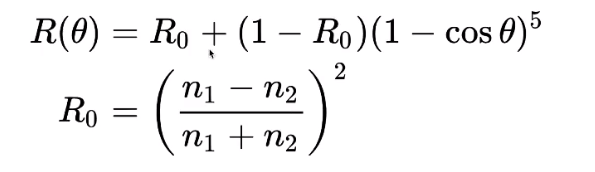
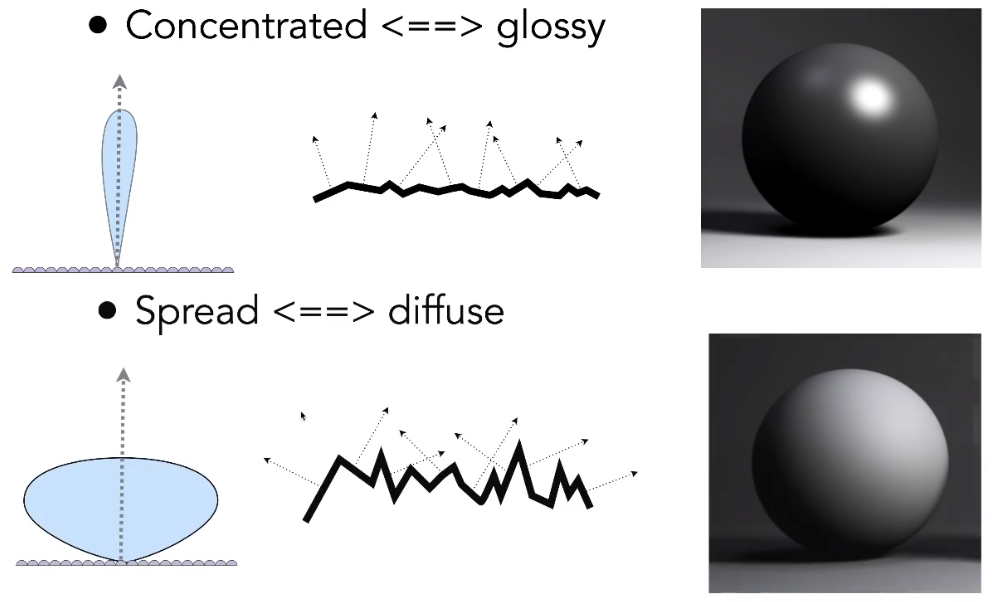
# Normal Distribution Function(NDF)
描述微表面的发现分布。
# Beckmann NDF 模型
类似高斯函数:
- :用于描述法线分布的「粗糙程度」,「粗糙程度」越小表示越接近镜面反射,分布函数越窄。
- :半程向量 和法线 的夹角。
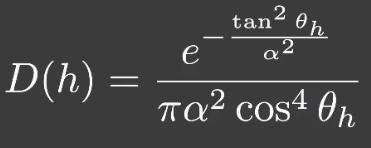
公式内 中的 实际上是对 做的一个映射,这样就可以把有限的 映射到无限大的 域内。并且在 超过 的情况下不会有值。这样就可以只统计半球区域了。
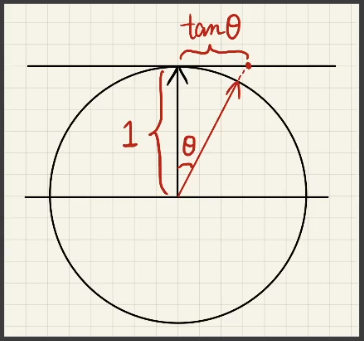
公式内 的作用是对结果进行归一化,希望最终的分布图在够映射到一个 1 x 1 圆内的同时,满足圆内各点的积分为 1。
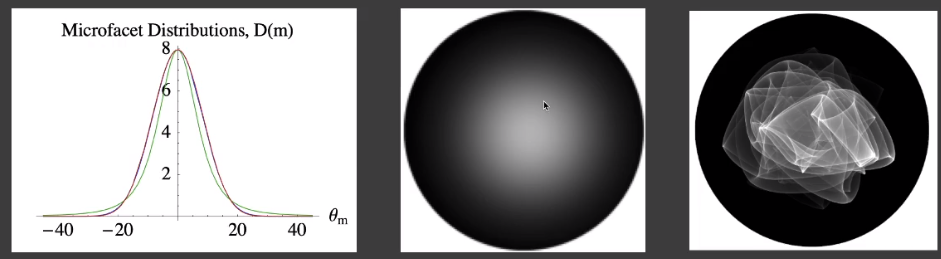
# GGX NDF 模型
「GGX」具备一个特性:「long tail」(长尾)
「长尾」的好处在于,在半程向量和法线夹角不断增大的过程中,光线强度的过度比较柔和。
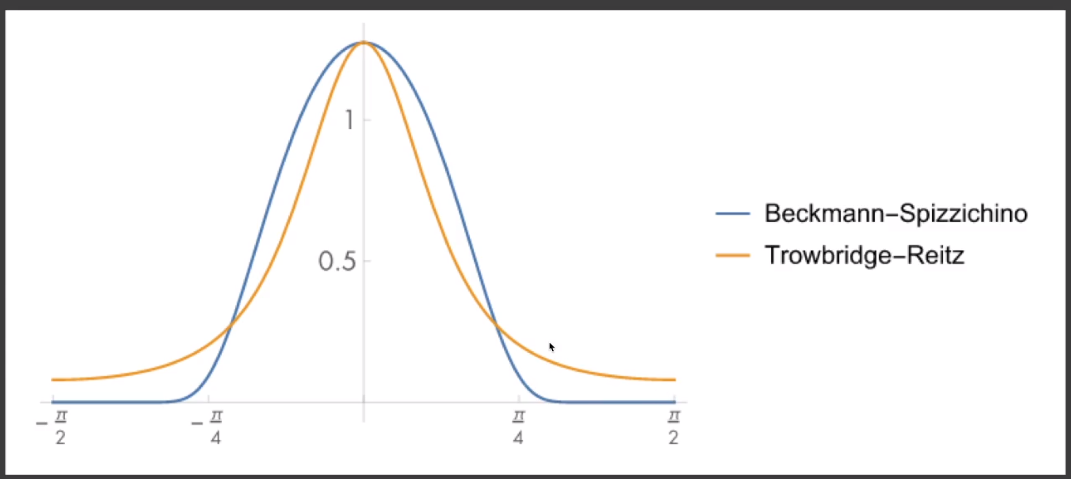

# GTR(Generalized Trowbridge-Reitz)NDF 模型
引入了一个 变量,同过其控制「长尾」长度。
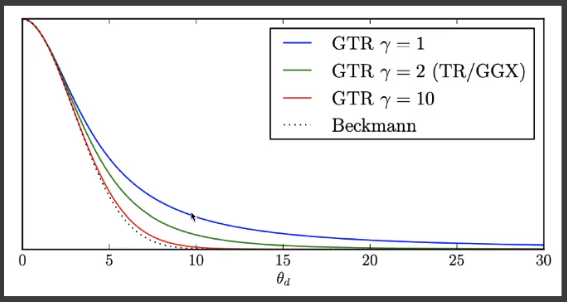
# Shadowing-Masking Term
用于解决微表面之间的「自遮挡」问题,对于某些位置需要进行一定的「暗化」操作。

遮挡光线的被称为「Shadowing」,遮挡视线的被称为「Masking」。虽然两者存在联系,单方便起见一般单独考虑:
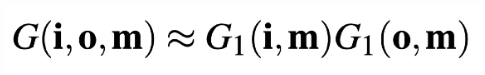
由于「自遮挡」在「观察方向」垂直于「法线」方向时最为剧烈,反之「观察」方向和「法线」方向平行时几乎为 0,因此可以定义一个用于描述「自遮挡」的函数来达到更加真实的效果。
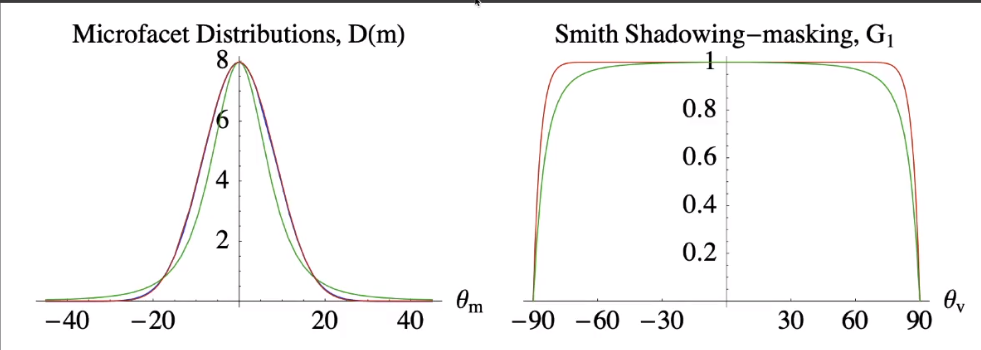
「自遮挡」项的引入虽然能够解决画面边缘过白的问题,但是另一方面,由于只考虑了一次自遮挡(没考虑遮挡后的反射),这会使得在法线分布越「粗糙」的情况下,由于「自遮挡」而丢失的能量会越发的多,从而画面整体更暗。


如何才能够补回原来丢失的能量呢?
- 计算多次弹射「Multiple Bounces」:很慢,在实时渲染中不太适用。
- Kulla-Conty Approximation:工业界常用的解决办法。
# Kulla-Conty Approximation
对求面的积分函数如下:参考 GAME101
那么如果要计算一个 2D 的「BRDF」反射出的总能量,只需要积分球面上每个点对应的立体角内接收并反射出的能量。
其中 是「BRDF」项。
这里假设 为 1,并且 可简化为 ,然后把 视作 ,这样积分域也从 。

因此,在一次反射之后,会损失 的能量。加上一部分自遮挡,因此需要考虑两次。
加入系数 ,并对原公式进行一定程度的简化,系数 的定义:
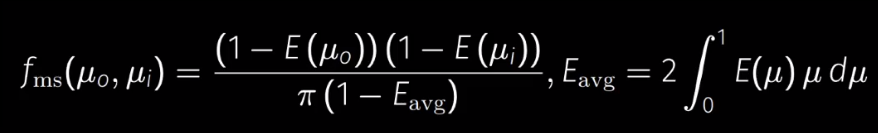
把系数带入公式的最终结果:
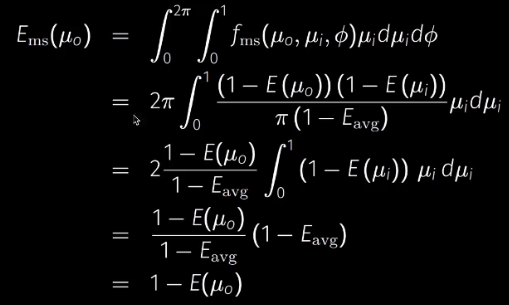
但是 未知,因此需要计算。
为了简化计算开销,可以预先对 进行预处理。根据公式可以计算出不同情况下 和 的 。
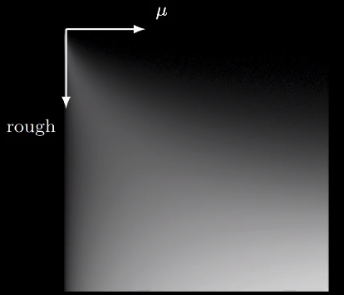
# Result
加入补偿项之后的结果对比。

# What if the BRDF has color?
考虑颜色的情况下,「能量损失」 == 「被物体吸收的颜色」
定义一个 「Frensel Term」用于定义平均每次反射所损失的能量。
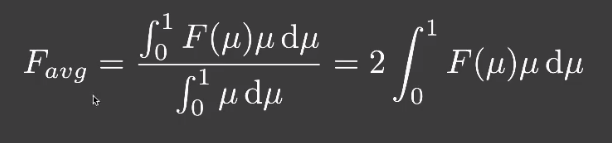
因此,直接看到的物体表面的光线就是 。
而没有被看见,并继续被反射一次的光线将会是 。
继续被反射一次并且能够被看见的光线则是 。
...
最终经过 k 次反射并且能够被看见的能量将会是 。
然后再把所有的能量相加,最终就可以得到「颜色项」(color term):
然后直接用没有考虑颜色的计算出着色的「BRDF」结果乘上这个「颜色项」就能得到颜色。—— 这里的 和 都是三维向量,因此可以得到一个 rgb 的通道值。
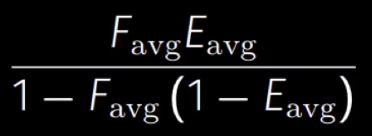
# Calc Color Result

# Shading Microfacet Models
# Linearly Transformed Cosines(LTC)
「LTC」用于解决微表面模型的渲染:
- 主要应用于「GGX」的模型,其他模型也能正常工作。
- 不考虑阴影。
- 处理面光源是「多边形」的情况。
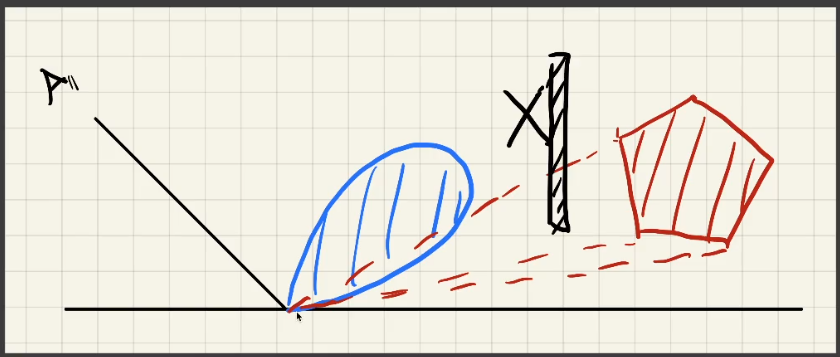
# Key idea:
- 考虑采用一种变换规则,把任意微表面的「BRDF」的 lobe 转为 cos 形式的微表面的 lobe。
- 并且对应的光源经过类似变换得到一个新的光源。
- 这样做的好处在于:最终得到的在 cos 上的积分是有解析解(analytic)的。
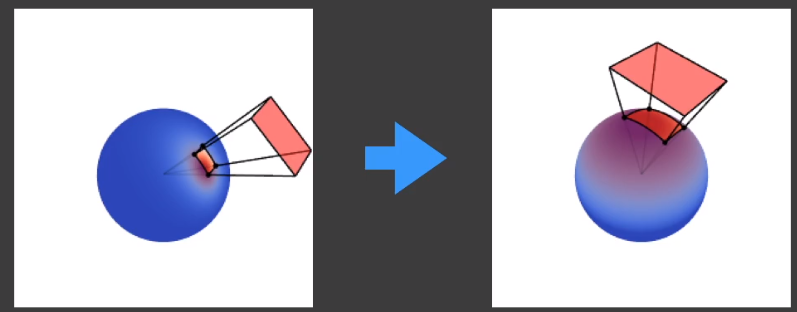
因此,任意的「BRDF」都可以通过一个 变化转变为 cos 的分布。
再针对所有的从光源到物体的光线方向都进行类似的变换。
便能够计算出变换后的多边形光源。
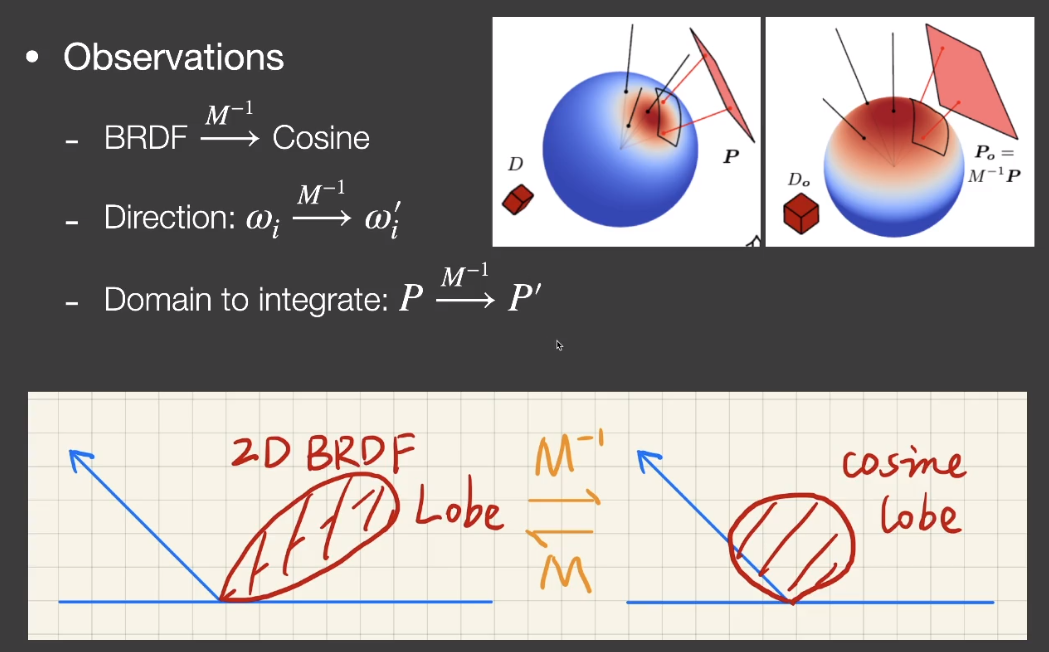
# Approach:
假设面光源的任意位置的光线强度都是一样的
- 把入射光方向替换为 cos 形式的变换方向。
- 再进行「雅可比变化」,把 转化为 的形式。
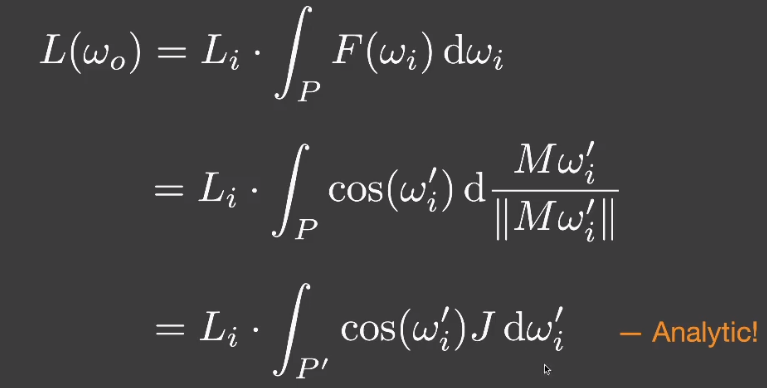
# Result

# Disney‘s Principled BRDF
- 「Mircofacet BRDF」对于物理材质的模拟不真实
- 复合材料情况下,既有 diffuse 又有 glossy 时,微表面不能很好的处理
- 「Mircofacet BRDF」对于设计者来说不太友好
- 「Principled BRDF」虽然并不一定在物理上正确,但效果尚可且对艺术家友好。
# What is 「Principled」
「Principled BRDF」的涉及遵循以下几个原则:
- 使用更加直观的参数来代替物理参数。
- 参数数量应该尽可能的少。
- 参数应该有一个合理的范围区间(0~1)。
- 并且支持在某些情况下,可以让某些参数的数值超于阈值,以便达到艺术家想要的效果。
- 参数的组合应该尽可能健壮,避免不同组合的情况下导致程序崩溃。
# How does it work
下图表示了单个参数不同取值情况下对画面的影响。

# Pros and Cons
- 容易调整,易于理解。
- 不同参数组合可以达到多种材质效果。
- 实现开源可用。
- 不基于物理,但无伤大雅。
- 参数之间存在交叉。
# Non-Photorealistic Rendering(NPR)
给画面一些风格上的渲染,使得整体表现上更趋于艺术。
# What is Photorealistic Rendering
接近照片拍摄的效果。正确的光照、阴影、几何。

# Outline Rendering
- 「B」Boundary /border edge:物体的外边界。
- 「C」Crease:内部的折痕。
- 「M」Material edge:材质的边界。
- 「CS」Silhouette edge:物体的外边界,且有多个面共享的。
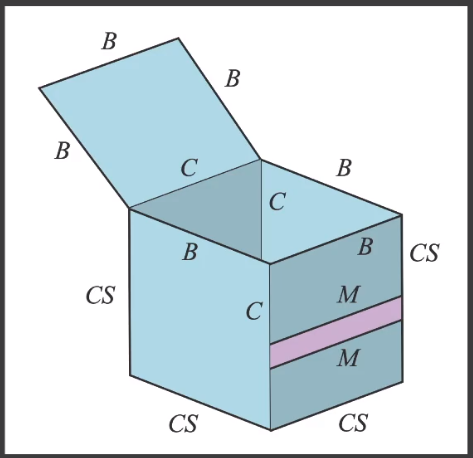
# Outline Rendering —— Shading
Shading normal contour edges
对观察方向和法线方向垂直的部分进行涂黑,不过没办法保证边缘粗细一致。

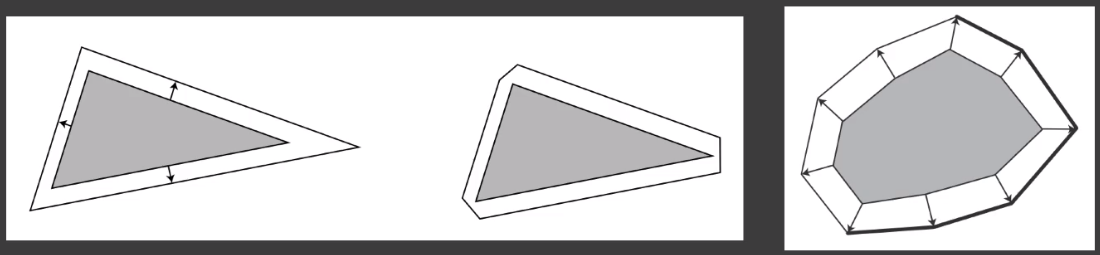
# Outline Rendering —— Geometry
Backface fattening
- 对背朝观察方向的三角形,都往外扩一圈,然后进行渲染。
- 由于背面的三角形都会大一些,而且背面三角形本身就看不见,因此渲染出来也是黑的。
# Outline Rendering —— Image
Edge detection in images:
通常会使用「Sobel detector」来做图像的「filtering」
- 让左右分界更加明显

- 让上下分界更加明显

# Color blocks
锐化色块之间的边界。
- Hard shading:thresholding on shading
- Posterization:thresholding on final image color
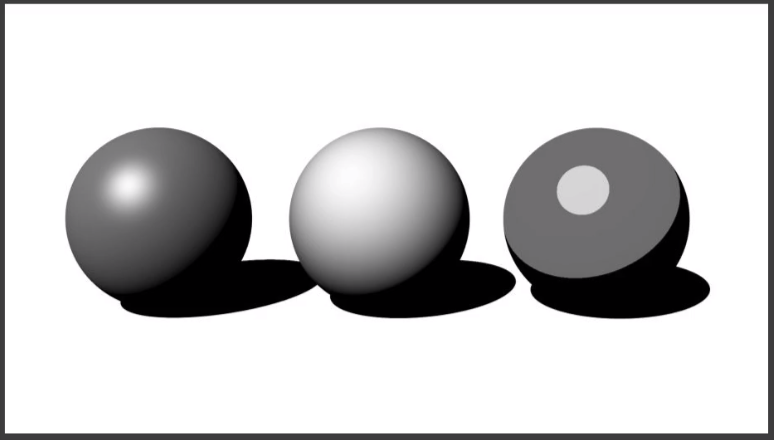
「Quantization」不仅仅可以用于非黑即白的画面,多级的渐变也可以。

还可以在不同的部位应用不同的渐变规则。

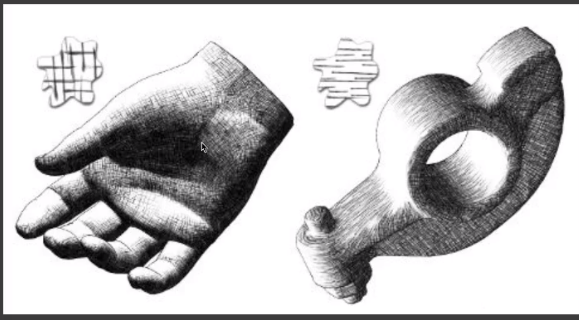
# Strokes Surface Stylization
把阴影强度替换成方格线密度的形式来展示素描的效果
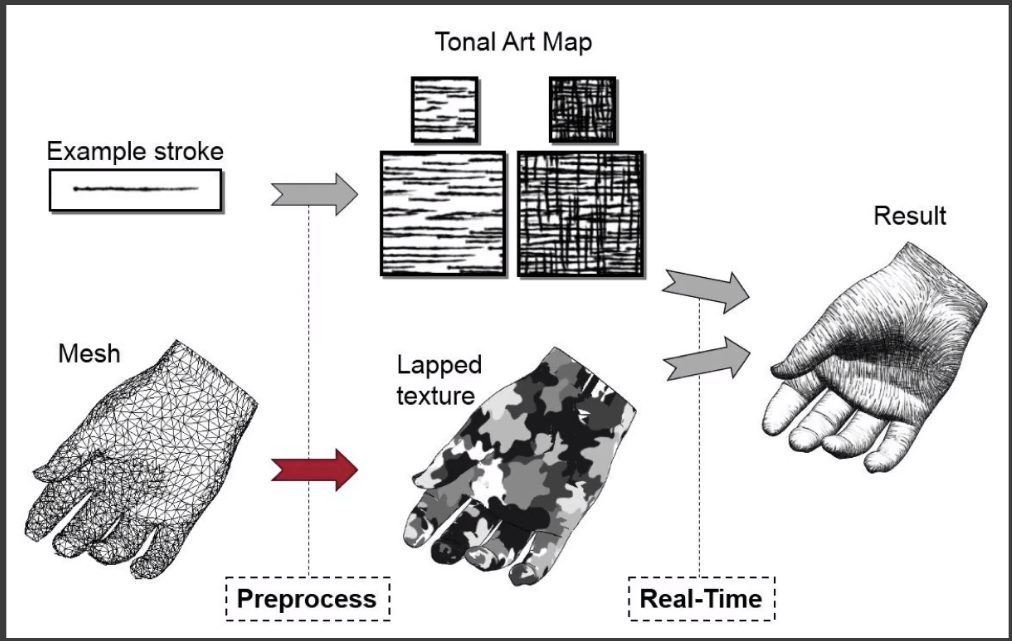
# Tonal art maps(TAMs)
- 预先定义好不同密度的问题
- 并且生成对应的「MIPMAP」

# 关键字:
- lobe:定义为由微表面上某个点的入射光所对应出的反射光的分布区域所形成的花瓣状区域。