以下为个人学习笔记整理,课程官网传送门,作业传送门,会议系统传送门。
# Real-time Shadows
- Shadow mapping
- The math behind shadow mapping
- Percentage closer soft shadows
- Variance Soft Shadow Mapping
- MIPMAP and Summed-Area Variance Shadow Maps
- Moment shadow mapping
- Distance field soft shadows
# Shadow mapping
- 2-Pass Algorithm:详细说明见 Game101 Shadow Mapping
- 【Pass1】The light pass generates the SM(shadow mapping):从点光源出发,记录每个点的深度值
- 【Pass2】The camera pass uses the SM (recall last lecture):从摄像机出发,如果两者深度值相同,则可以被看见,否则视作阴影。
- 【优点】:可以用 SM 对场景阴影进行表示,不需要场景实际的几何。
- 【缺点】:有走样(锯齿)和自遮挡现象「self occlusion」。
# self occlusion
由于光源向四周发出光线并记录深度的过程中,存在一个精度问题,并非每个点拥有一个深度值,而是某块范围拥有一个深度值,这种情况下将导致距离非常接近的两个点会存在互相遮挡的情况。

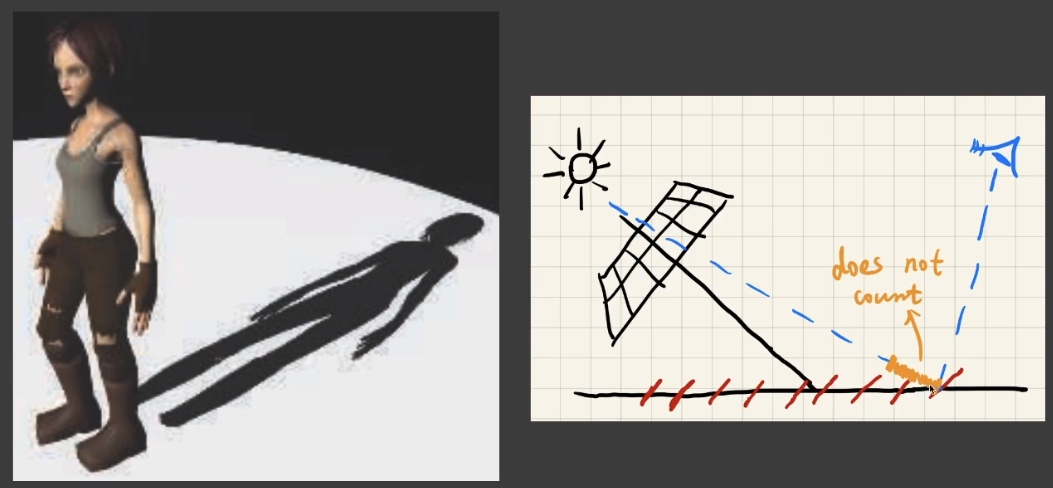
# Adding a bias to reduce self occlusion
增加一个误差值可以有效的降低自遮挡带来的问题,但是会让原本产生阴影的部分出现丢失。
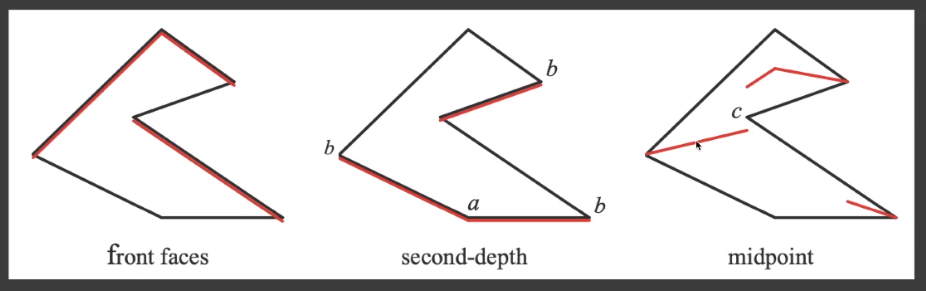
# Second-depth shadow mapping
引入第二深度的概念,在一张 shodow mapping 中存储「最小深度」和「第二小深度」的中间值。
如果某个点的深度大于「中间值」或者小于「中间值」,那么它将会被遮挡或显示。
这样做也会有一些问题:
- 所有物体必须有厚度,因为需要取到第二深度,如果物体只是一个面,那也毫无意义。
- 对于实时渲染来说,开销不值得。
- 有很多多余的
if判断。 - 有很多需要修改最小和次小深度的操作。
- 有很多多余的
RTR does not trust in COMPLEXITY
# Aliasing

# The math behind shadow mapping
# Approximation in RTR
在实时渲染中,一些复杂的计算过程往往会通过一些近似的方程所替代,从而提高运行效率。
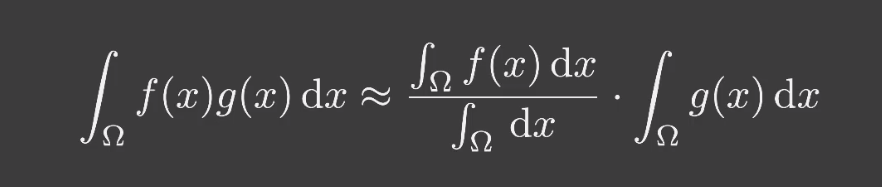
何时是近似的?
- 在
g(x)的 max 和 min 越接近的时候。 - 在
g(x)的有效积分域越小时。
# In Shadow Mapping
把该性质应用于光照方程,把「Visibility 函数」单独进行积分,这样就可以视为「Visibility 函数」积分 ×「shading」
- shading:所有光源的光线照射到该点的强度,这部分内容可以记录在 shading mapping 内。

计算光照的时候,何时是近似的?
- 当积分域很小,换句话说就是该点所接收到的光线范围很小:
- 点光源 or 方向光源情况下,积分域很小。
- 当函数曲线变化平滑(Smooth)时,换句话说光照在各个区域的强度变化不大:
- :物体本身的材质「BRDF」是 diffuse 的。BRDF 相关介绍
- : 有着恒定强度的光照的情况下。
# Percentage closer soft shadows
# Percentage Closer Filtering(PCF)
最初被用于抗锯齿,后来被用于制作软阴影(PCSS),主要原理是对一块范围内的阴影求平局(类似模糊效果)
filtering 操作不直接处理 shadow map:
- 对深度贴图做模糊处理,最终的阴影效果依旧是非 0 即 1,锯齿任然存在。
- 不是对已经存在锯齿的结果进行 filtering 操作,也不是对着色的结果做 filitering。
处理办法:
- 针对某个点,对其周围一定范围内的「shading point」和对应点的 「shadow map 深度值」进行比较,得到 0 or 1 组成的集合,再求平均。
- 「shading point」:从摄像机方向观察到的点周围的点。
![image-20210602191149305]()
PCF 不是对最终的阴影做模糊操作
最终的阴影做模糊,最终的效果依旧还是会有锯齿

用 PCF 处理后的图片

当求平均的范围变得很大时,就实现了软阴影的效果
# Percentage Closer Soft Shadows(PCSS)
决定一个阴影究竟是软阴影还是硬阴影,取决于阴影和物体的距离
- Filter size(range)<-> blocker distance

点光源是不存在软阴影的,只有面光源才有软阴影,而且只有点光源才会有 shadow map。因此很多情况下,通常会用点光源生成 shadow map,然后视作面光源来做软阴影。
# Relative average projected blocker depth
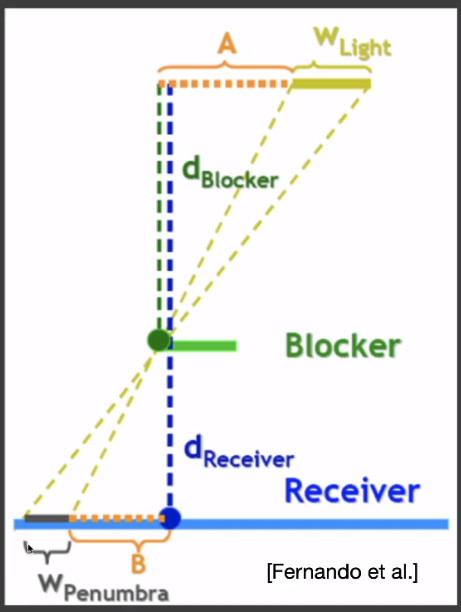
# PCSS algorithm
- 【step1】Blocker search:已知一个 「shading point」,通过点光源和「shading point」得到对应「shadow map」上的一个点。判断该点是否被遮挡,如果被遮挡,则该点为「blocker」,记下它的深度值。最终得到一张记录了所有「blocker」深度的图。再针对某个「blocker」,取其一定范围内的所有「blocker」的深度求平均。得到「average blocker」。
- 【step2】Penumbra estimation:通过「average blocker」计算出「filter size」。
- 【step3】Percentage Closer Filtering:用计算得到的「filter size」去对该点进行「PCF」处理。
# 思考:求「average blocker」所需的范围该是多大呢?
- 通过「light size」决定。
- 通过「shadow map」和 「light」的距离决定。
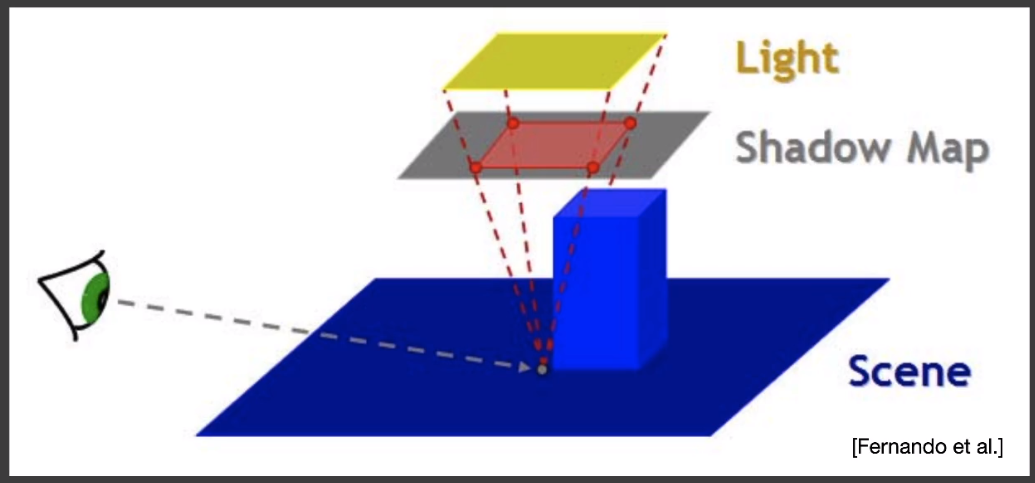
# A Deeper Look at PCF
- Filter / convolution:
- :点
p邻域范围。 - :对
p点周围的点q,根据点q和点p的距离进行加权。
- :点
# In PCSS
- :表示符号函数。 如果大于 0,最终的结果就是 1; 如果小于 0,最终的结果就是 0。
- :表示点
q「shadows map」 的深度和 「shading point」 的深度差,一般表示「shading point」x是否被遮挡。 - :用来判断点
p周围的点q是否被遮挡。
因此 PCF 并不是对 「shadows map」 做 「filtering」:
如果对 「shadows map」 做 「filtering」,最终的 只能是非 0 即 1。
同样,PCF 也不是对图像的最终结果做「filtering」:
# Variance Soft Shadow Mapping
VSSM 用于解决 PCSS 效率低下的问题。[Fast blocker search【step1】and filtering【step3】](#PCSS algorithm)。
# Fast【step3】
【step1】和【step3】比较慢的地方在于求某个区域内数值的平均。以【step3】这项操作为例,求区域内遮挡 1 和未遮挡 0 的平均,可以进一步理解为,区域内 1 的占比。
因此原本需要求得一个范围内「遮挡」和「未遮挡」的平均变为需要知道一个区域内,比「shading point」深度值大的点(遮挡)的占比。
# 如何求得比「shading point」深度值大的点的占比呢?
- 首先,我们假设深度值的分布是符合正态分布的,或者说近似正态分布。
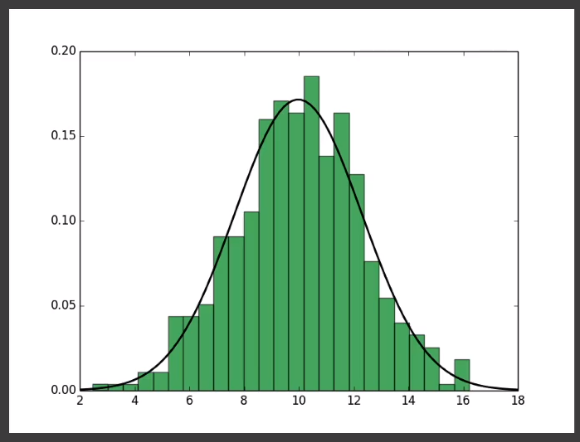
为了确定一个正态分布曲线,需要知道样本的「均值」和「方差」
如何得到样本的「均值」?
- 「MipMap」本身就是一个很好的求均值解决方案(但仅限矩形区域,且不够准确)。
- Summed Area Tables(SAT)
如何得到样标的「方差」?
:方差 = 平方的期望 - 期望的平方。
- 期望的平方:可以用上述求得的「均值」。
- 平方的期望:需要另外一张「shadow map」用于存储深度的平方,之后再通过上述方法求其均值。
因此,需要单独一张「shadow map」用于存储深度的平方。
得到了曲线的正态分布,接下来就需要求占比了
- 通过正态分布的 「PDF(Gaussian Distribution Function)」 曲线,求得 「CDF(Cumulative Distribution Function)」 曲线,便可以获取占比。
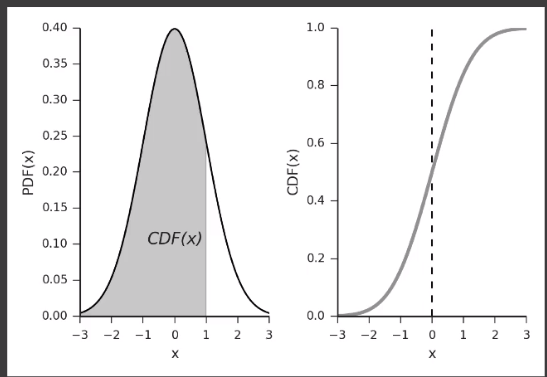
# 不是正态分布咋办?
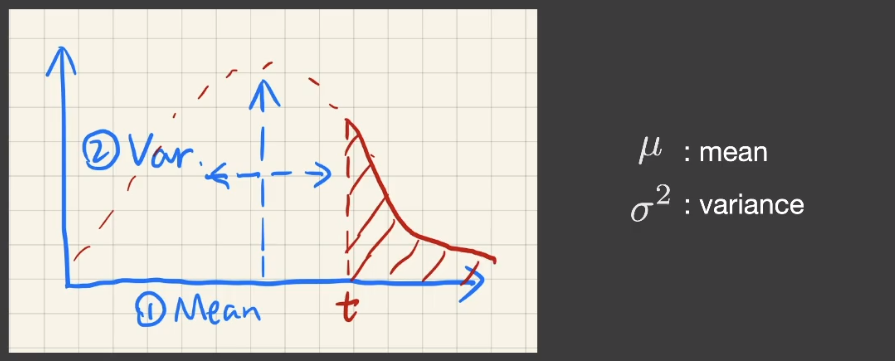
万能的近似函数又来了,为了能够满足任何分布曲线。「CDF」曲线可以用「切比雪夫不等式」转成通用格式:
该函数可以满足任何分布曲线,但是有一定程度上的误差,且如果 t 在分布函数的左半侧,结果会更加的不准确。
# 总结 Fast【step3】
预处理
- 得到一张记录深度的「shadow map」。
- 得到一张记录深度平方的「shadow map」。
运行时
- 获取某点的深度平均值「MipMap」。O (1)
- 获取某点的深度平方的平均值「MipMap」。O (1)
- 得到占比概率([Visibility 函数](#In Shadow Mapping))。O (1)
- 干掉了采样和高消耗的循环。
缺陷
- 不支持实时情况下的深度变化,如果有深度变化需求需要动态修改「shadow map」
# Fast【step1】
【step3】的优化告一段落,接下来看【step1】的问题。【step1】需要查询周围的「blocker」并且需要求出所有「blocker」的「平均深度」。
- 需要对每个「块」进行遍历,效率低下。
- 需要对所有「blocker」深度求平均。
- 特别注意:「blocker」是被遮挡的「块」,即深度值小于「shadping point」的「块」—— 图中蓝色部分。
假设「shadping point」的深度是 。
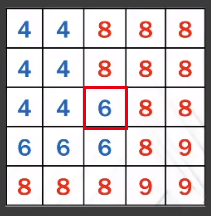
- Blocker(z < t)的平均值记为 。
- Non-blocker(z > t)的平均值记为 。
- 因此,可以推导出如下公式:
- 表示 Non-blocker 数量
- 表示 Blocker 数量
# 未知,如何求?
需要计算 ,其中 均已知。
- 不妨做个大胆的假设:。
- 最终: Z_{occ} = \frac{NZ_{Avg} - N_1t}
# MIPMAP and Summed-Area Variance Shadow Maps
# MIPMAP
MipMap 的介绍可以回顾 Game101 的 Texture Mapping。
MipMap 有几个缺陷:
- 处理均值采用的是切分网格形式的平均。因此,被切分出的网格内任意一点的范围平均都是同样的结果,并不是真正意义上的取某个点周围的一定范围进行平均。
- 对于非矩形的区域没有办法很好的支持。
- 对于矩形区域,如果边长不是
2的阶乘,例如6,这样就需要对4和8来做三线性插值。
# Summed Area Tables(SAT)
# Prefix sum algorithm
「SAT」的核心在于前向求和算法,假设输入的内容是一个一维数组,经过前向求和算法后会得到一个新的一维数组,数组内每个元素记录的是前面 N 个元素的总和。因此,计算中间某 X 个连续的数只和将变得非常简单。
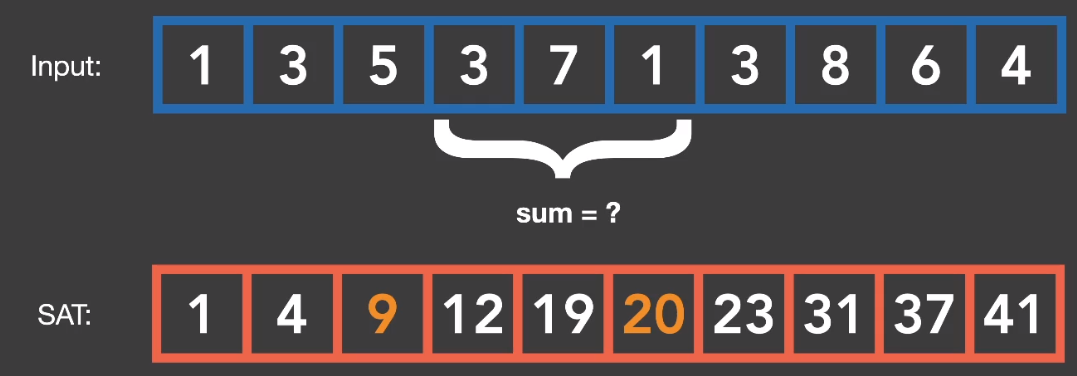
一维数组内的求和解决了,接下来思考一下二维数组应当如何处理呢?
原理类似,每个点距离一个从远点到该点组成的矩形面积的数据总和。通过类似求面积的方式,最终就能得到某个点的周围一个矩形空间内的点总和。
「蓝色方块」的面积便可以这么计算:「蓝色方块」=「大绿色方块」-「两个黄色方块」+「绿色小方块」

# 总结
- 「SAT」计算结果非常准确。
- 需要额外 的空间存储「SAT」。
- 求解平均值速度提升到了 。
# Moment shadow mapping
「MSM」用于解决「VSSM」的误差问题,「VSSM」的很多计算都是基于「正态分布」实现的,换句话说,如果分布曲线不是接近「正态分布」的情况下,结果将变得不准确。
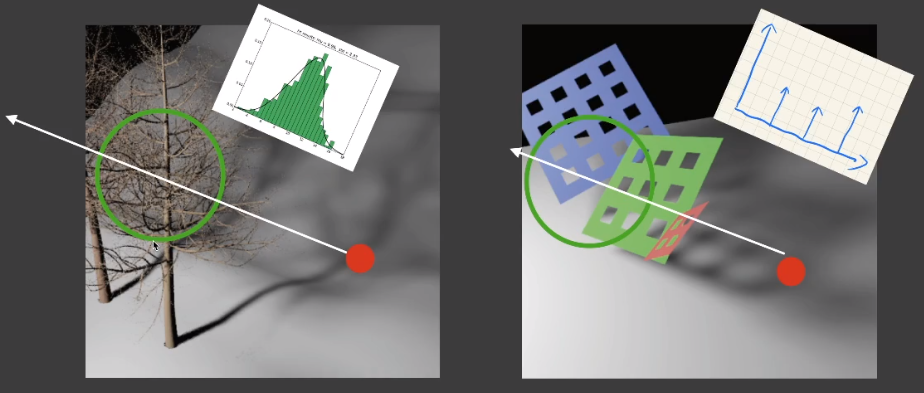
# 【Issues1】深度值不符合正态分布
深度值不符会使得「Visibility 函数」的结果不准,最终会使得画面偏暗或者偏亮
- 偏暗:这种情况下还能够接收。
- 偏亮:偏亮则会出现漏光效果。阴影的某块区域会比周围更亮
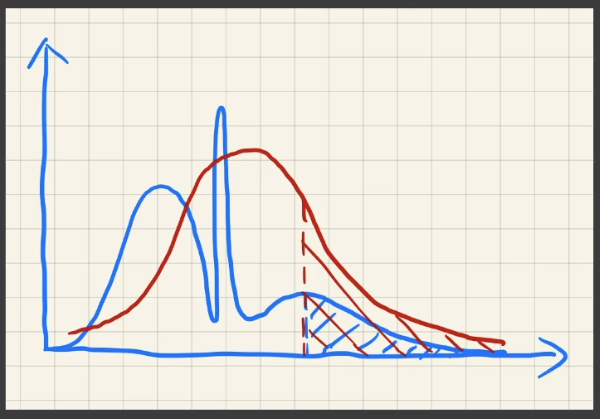
Light leaking

# 【Issues2】由于「切比雪夫不等式」的特性, t 在分布曲线左侧时误差会非常大。
non-planarity artifact
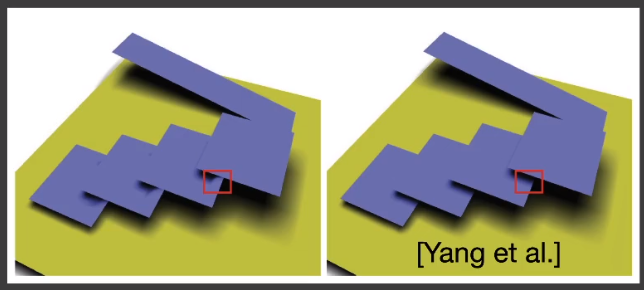
# 目的
「MSM」主要是用来解决非正态分布情况下「VSSM」带来的误差【Issues1】。
为此,「MSM」引入了一个「higher order moments」来描述一个分布。
# Moments
由于「VSSM」的「正态分布曲线」是通过均值和均值平方计算得到的。因此可以成「VSSM」使用了 两种「moments」。「MSM」则是想通过使用更多的「moments」让结果变得更准确。
# 结论
如果用前 n 阶「moments」,便可以表示 阶的函数。
「PCF」函数本身是个 2 阶函数,由于「PCF」的结果比较准确。如果想要「VSSM」结果接近「PCF」,则需要使用前 4 阶「moments」。
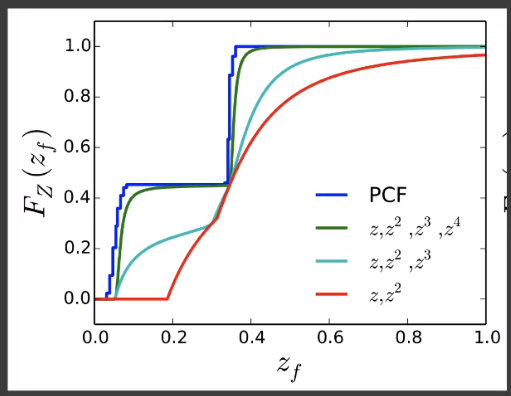
# 总结
理论上越多个「moments」能达到的效果将会越好。存储上可能会有一定的消耗,另外:如何根据前 n 阶「moments」得到近似「PCF」(有两个台阶)的函数也是一个非常复杂的问题。

# Distance field soft shadows
「SDF」是一种更加高效的计算软阴影的实现方案。

# Distance Functions
定义空间中每个点到最近的一个物体表面的距离(带正负号)

# Blending Support
距离函数(Distance Functions)支持对多个简单的几何物体的距离场做「Blending」得到复杂几何物体的距离场
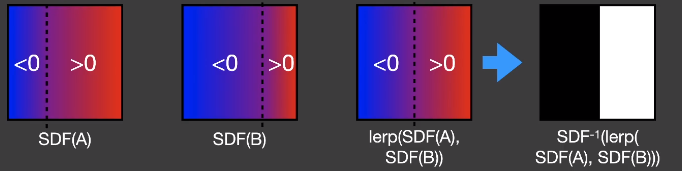

# Usages of Distance Fields
# 【Usage1】:Ray marching(sphere tracing)to perform ray-SDF intersection。
核心目的是用于对射线求交。
- 获取起始点的 「Distance」,获得射线的传播方向「Distance」距离的下一个点的「Distance」并继续推进。
- 移动一定距离后或者遇到某个物体表面时,算法结束,便可以快速获取射线是否命中物体表面,在射线碰撞检测方面使用较多,效率高。

# 【Usage2】:Use SDF to determine the(approx)percentage of occlusion。
核心目的是求得视锥的「可视率」。该情况下「Distance」一般不带符号
- 从「shading point」往某个方向查询,中间遇到了「Distance」不为 0 的点时,记录一下,直到遇到遮挡或者光源时停止。

- 视锥范围就是「Distance」不为 0 的点和「shading point」形成的最小切线角度 。
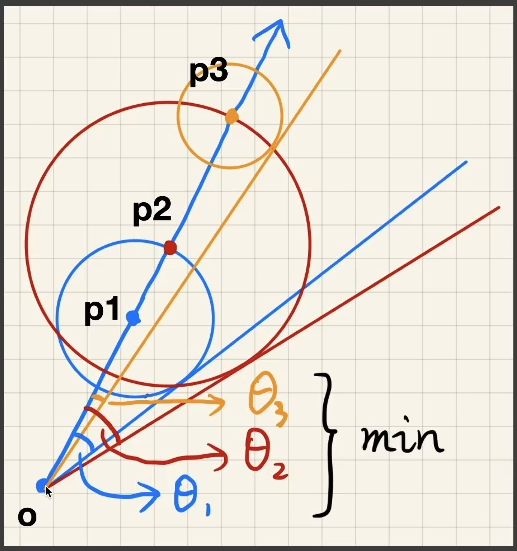
- 视锥的「可视率」就是 ( / 整个视锥角度)。
# 如何提高「可视率」计算效率?
还是老办法,用一个近似函数来代替~

并且引入一个系数 k 用于调节整个系统的「敏感度」,即:什么时候完全在阴影内,什么时候完全不在。
- 如果
k = 100,那么超过0.1以上的「可视率」就可以认为是完全不在阴影内,这样的效果会让阴影变得更加「硬」,边界分明。 - 同理,如果
k = 2,那么超过0.5以上的可是「可视率」才能认为是完全不在阴影内,剩下的地方都是从非阴影到阴影的过渡,这样的效果就更像「软阴影」。

# Distance Field:Visualization
针对场景中每个物体计算「Distance Field」,然后对图内每个点取所有物体内记录该点「Distance」的最小值作为「Distance」的最终值。

# 总结
「SDF」的优点:
- 速度快
- 高质量
「SDF」的缺点:
- 需要预处理
- 需要庞大的存储空间
# Antialiased / infinite resolution characters in RTR
基于距离函数的无锯齿字符