以下为个人学习笔记整理,课程官网传送门,作业传送门,会议系统传送门。
# Real-time Environment Mapping
环境光照认为所有的光线都是来自「无限远」的(所有光线强度是相同的)。
# Shading from Environment Lighting
环境光也被称为「Image-Based Lighting」(IBL)。
# How to use it to shade a point(without shadows)?
- Solving the rendering equation:由于环境光不考虑阴影(遮挡)因此不需要计算「Visibility 函数」

- General solution - Monte Carlo Integration GAME101 蒙特卡洛积分
- Numerical
- Large amount of samples required
# Observation
渲染方程本质上就是对一个物体的半球进行「BRDF」X 「光照强度」的积分。
# BRDF 的特性:
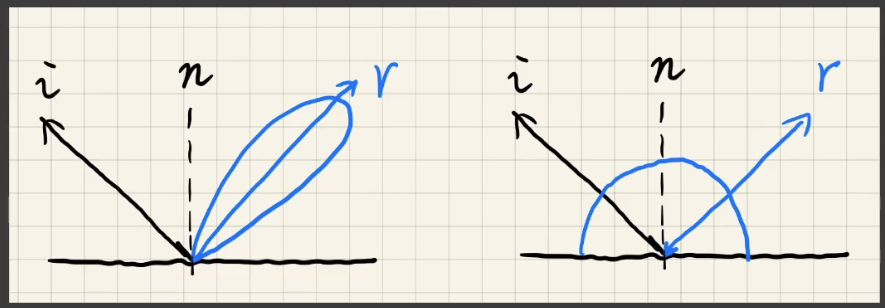
- 如果「BRDF」是非常光滑的,那么它的反射光线就更加的聚集(接近镜面反射),因此积分的有效区域就更小。—— small support!
- 如果「BRDF」是非常粗糙的,那么它的反射光线就更加分散(接近漫反射),但是反射到各个方向的光照强度却非常接近。—— smooth!
- 因此这里也可以对积分套用 GAME202 Shadow PCF 部分相同的近似函数进行近似,并且非常满足近似条件:
g(x)足够 smooth 。- 足够的 small support 。
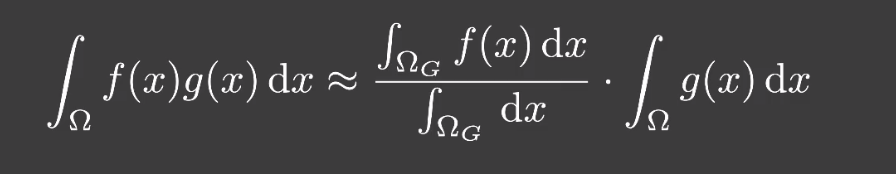
- 因此我们可以对渲染方差做一个近似处理:
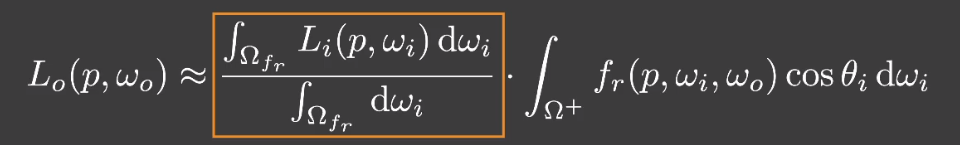
# The Split Sum
# 【step1】Prefiltering of the environment lighting
试想一下,需要对光照进行积分并且除以积分域。
- 如果积分域很小(BRFR 很光滑),那么「shading point」光照强度本身的值就可以作为积分后的结果。所以每个「shading point」的着色都接近本身的光线。
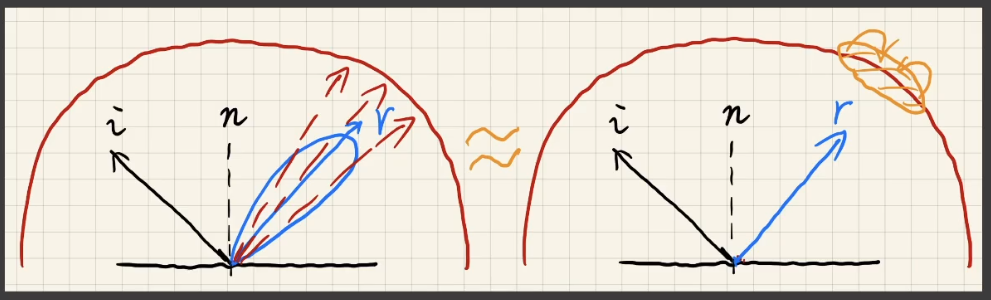
如果积分域很大(BRDF 很粗糙),并且光线函数非常的 smooth。「shading point」的光照强度就等于附近点的平均。那么对光照进行积分并且除以积分域后的结果体现在图片上其实就是对周围一定区域内所有像素点的颜色进行「filtering」。
因此就能够类似 MIPMAP 的方式预处理多种「BRDF」情况下的环境光效果,然后针对不同「BRDF」的物体,对两张环境光贴图进行插值获得环境光。类似 GAME101 Texture Mapping 三线性插值

# 【step2】Prefiltering of the environment lighting
解决对范围「BRDF」求积分
# Microfacet BRDF
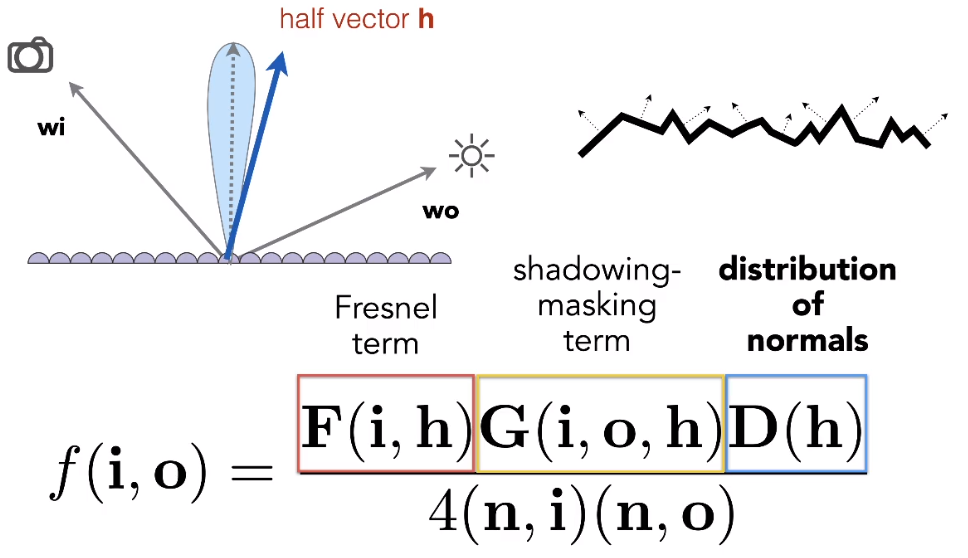
Fersnel Term
在菲涅尔项中,定义了入射角 和反射率()对反射结果的影响
- :定义为通过介质的光线中被反射的光线占比。
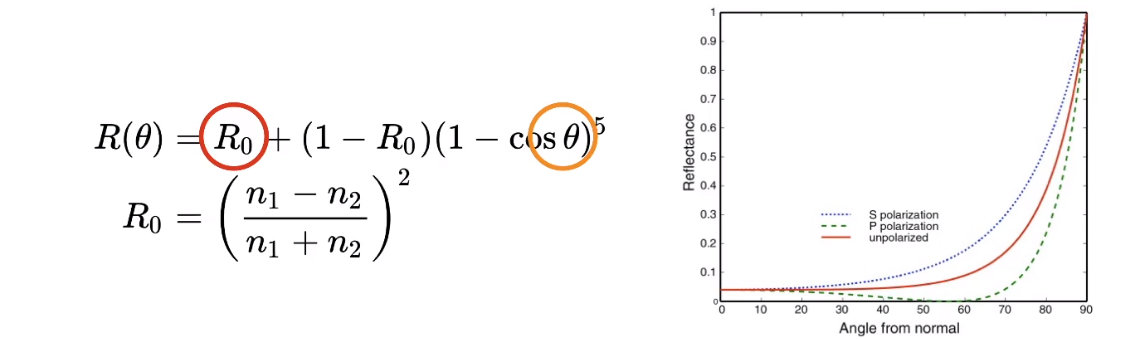
NDF Term
「NDF Term」定义了材质(微表面)的法线分布情况,其中 表示材质是光滑还是粗糙的,影响曲线宽度; 角度可以用入射角近似。
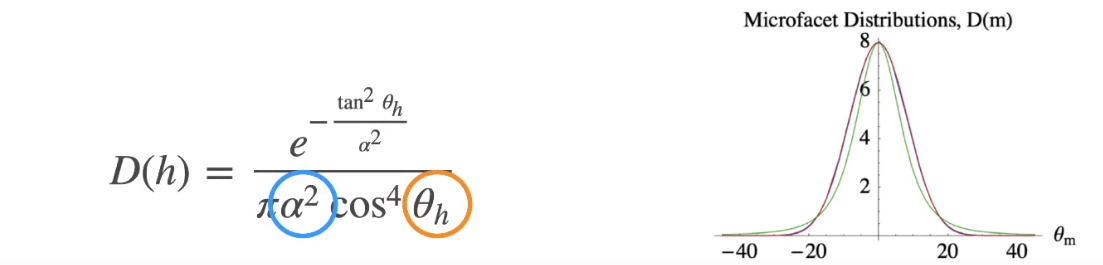
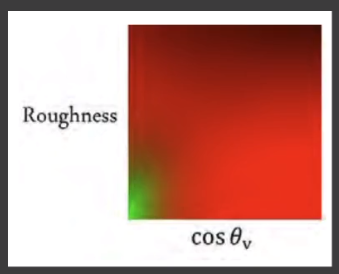
# Split again
由于「BRDF」还是太复杂,因此,决定对「BRDF」再次进行拆解。
- 把菲涅尔项里的 先拆出来

- 得到的两个积分项则可以不依赖反射率,因此可以对剩下的变量(粗糙度、入射角)进行预处理。
- 最终可以得到一张预处理后记录「粗糙度」和「入射角」的 2D 贴图。
# The Split Sum Approximation
- 最终的结果规避了采样的性能消耗,全部由预处理来完成。
- 速度得到了提升,并且非常近似之前的正常计算结果。

# Shadow from Environment Lighting
环境光阴影的实现相对较为困难:
- 环境光本身类似一个多光源问题,多个方向上的光线可以视作多个光源~,这种情况下生成的「shadow map」数量巨大,并不可行。
- 如果把环境光阴影的渲染视作一个抽样问题,想要用近似处理将不再准确,因为不满足其两个条件(要么 「small support」 要么 「smooth」):
- 环境光的渲染方程中「Visibility 函数」的计算比较复杂,每个点都得考虑周围半球的遮挡情况。
- BRDF 如果粗糙还比较好处理,但是光滑的 BRDF 就没有那么「smooth」了。
- 本身也并非「small support」的,环境光的光线来自于半球内任何方向。
# Industrial solution
工业上一般的解决方案:用最亮的一个或者多个光源来产生阴影。忽略掉其他的小光源。
# Related research
- Imperfect shadow maps
- Light cuts
- RTRT(might be the ultimate solution)
- Precomputed radiance transfer
# Fourier Transform
GAME101 傅里叶变换介绍。「任何函数」都可以通过一系列的 sin 、 cos 函数来表示。
# general understanding
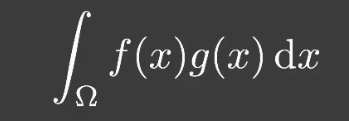
- 「filtering」操作可以理解为做了一个「卷积」
- 「Low frequency」 == 「smooth function」 / 「slow changes」
- 多个函数乘积积分结果取决于较低频率的函数
# Basis Functions
「基函数」的定义是:可以通过「基函数」的不同组合,来表示任意的函数
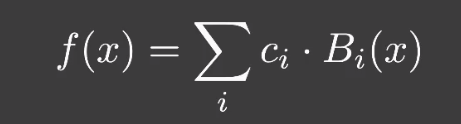
- 傅里叶级数也是一组「基函数」
- 多项式级数也是一组「基函数」
# Real-time environment lighting(& global illumination)
# Spherical Harmonics
「球面谐波函数」是一系列的二维的定义在球面上的「基函数」
有点类似一维的傅里叶级数:

- 每个「球面谐波函数」 都与一个「Legendre」多项式有关
- 投影:「球面谐波函数」另一个性质是计算该「基函数」的 比较简单:
- 「基函数」可看作是「坐标轴」。假设一个 N 维向量需要用 N 维坐标表示,那么每个维度的表示结果就是「基函数」,而该 N 维向量在任意「基函数」的「投影」,就是求该「基函数」的 。而该 N 维向量,则可以通过多个「基函数」和「投影」乘积的和表示。

# SH properites
- orthonormal:正交性。一个基函数投影到任意的基函数上结果为 0,基函数两两垂直。
- simple projection /reconstruction:投影计算较为简单。只需要用该函数和基函数做一个「product integral」
- simple rotation:非常支持旋转。原函数旋转后的结果相当于对每个基函数做旋转并求和的结果,另外可以用同届的多个基函数组合来表示旋转任意角度的某个同届基函数。
- simple convolution:卷积非常简单。两个频域上各点的乘积等于图像和卷积核的卷积。GAME101 卷积
- few basis function:low frequencys,一般渲染中只用到了 3 阶。
# Perfiltering
「Perfiltering」+「single query」 = 「no filtering」+「multiple queries」,说明见 [The Split Sum](#The Split Sum)

# Analytic Irradiance Formula
- Diffuse BRDF acts lite a low-pass filter:漫反射的「BRDF」可以看成是一个低通滤波器。
一个比较好的性质就是如果用「球面谐波函数」来描述一个「Diffuse BRDF」,大概只需要三阶「基函数」即可 ——(0、1、2)就可以拟合的很好,后面几阶的 值已经近似为 0,对最终结果影响不大。
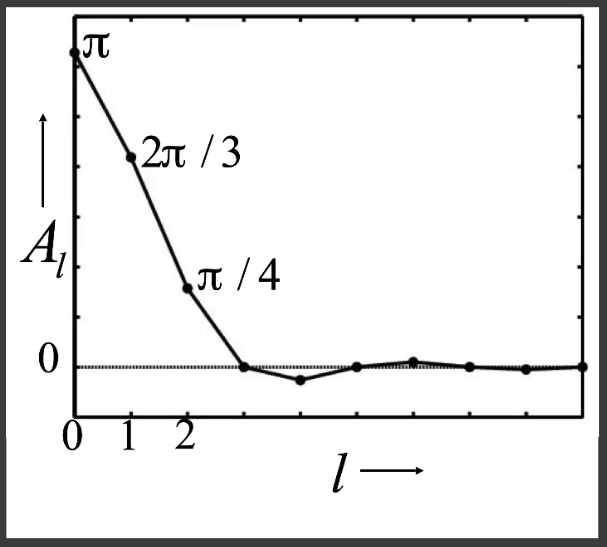
换句话说,由于「Diffuse BRDF」本身就只有三阶(低频),而两个函数乘积积分的结果取决于较低频的函数。因此
「Diffuse BRDF」X「」的积分结果更取决于「Diffuse BRDF」,而「Diffuse BRDF」只有前三阶有校,因此「」
也只需要考虑前三阶即可。
# 9 Parameter Approximation
分别用 「」的前三阶带入计算对于差异:
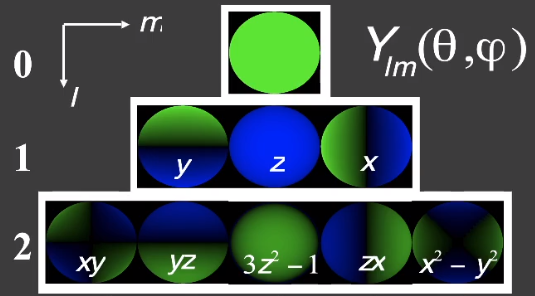
【Order 0】一个基函数

【Order 1】4 个基函数

【Order 2】9 个基函数

# In Real-Time Rendering(FYI)
只考虑「基函数」前三阶的情况下,方程最终可以简化为向量和矩阵的乘积在对向量点积。

以上内容都是在讨论「shading」而非 「shadow」
# Precomputed Radiance Transfer(PRT)
# Rendering under environment lighting
以下图的红点处为例进行环境光渲染:

可以通过该点预先得到以下预处理结果:
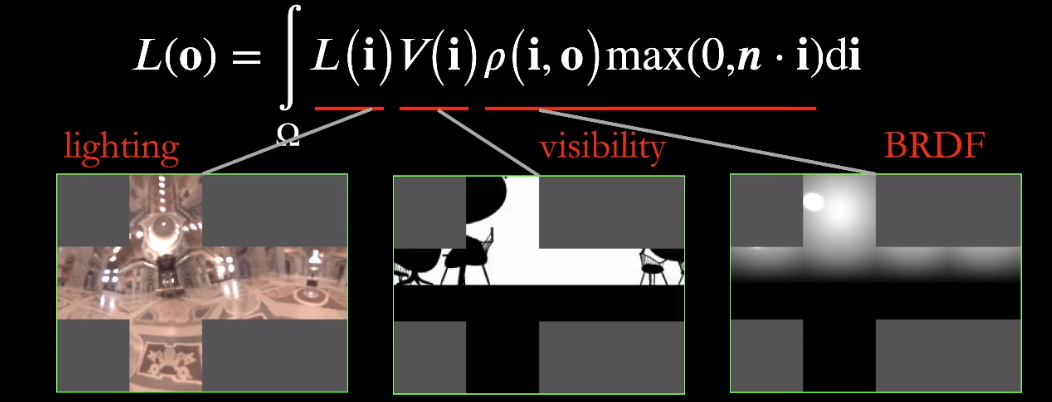
- lighting:可以对所有半球内的入射光线积分得到(球面谐波函数)
- visibility:对半球内的遮挡情况进行判断,可以用「shading point」对求面内所有方向都做一次 tracing 判断(球面谐波函数)
- BRDF:本身是个四维函数(入射方向 2 维 X 出射方向 2 维)。假如给定一个出射方向,该函数也会是一个和入射方向相关的函数 —— 和半球积分相关(球面谐波函数)
如果要计算一个点的光照,只需要把三个函数的结果乘起来在做积分。对应于三张图片相同位置的乘积和。
但是这样就意味着每个「shading point」都需要生成这样三张预处理的图片。
# Basic idea of PRT
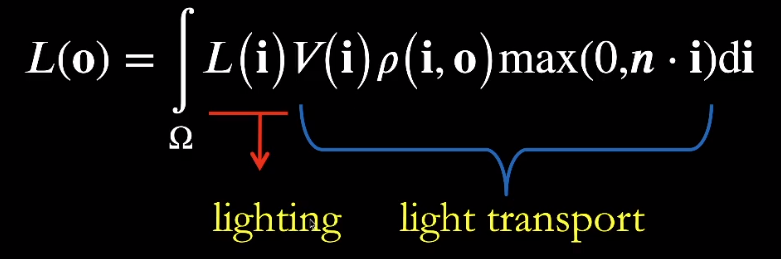
核心思想:由于「Visibility 函数」和「BRDF」在任何时间情况下都是不变的,能发生变化的只有「Lighting」。于是乎可以先提前计算出每个点的「Visibility 函数」和「BRDF」的乘积,这样就能少存一份贴图和运行时少算一次乘积。
# Diffuse BRDF Case
diffuse 情况下「BRDF」()本身就是一个常数,因此可以把公式写成如下形式。
- 再把 当作是一个「球面谐波函数」带入公式
- 并且把 和 提到积分外,近似处理
- 剩下的内容,其中 又表示 [「light transport」「球面谐波函数」投影到 上的系数](#Spherical Harmonics)

由于 参与预计算,所以是不能够在渲染过程中改变的,换句话说,场景内的物体是不可以移动的。
另外, 由于展开成「基函数」的描述, 项也已经在预计算中处理了,因此光源只能够新增或者减少(对应于公式中新增和减少 求和项),但是不能改变其中某一项的结果,比如调整光源方向。
值得一提的是:由于「SH」函数的旋转性质,[某个旋转过后的基函数可以用同阶基函数线性组合得到](#SH properites),又由于调整光源方向本质上就是对某个些基函数进行旋转,因此,对于旋转后的「SH」函数计算就可以转化为对同一个「SH」的基函数进行不同加权的求和操作。
经过「PRT」处理以后,原来需要用方盒记录求面光照的数据,就转换为记录基函数各阶的「系数值」,再计算「shading point」的时候,原来是用「lighting」x 「BRDF」的求面积分,现在则可以直接用基函数和系数的乘积和。

# 另一种推导:
把「lighting」和「light transport」都视为一个「SH」函数进行计算
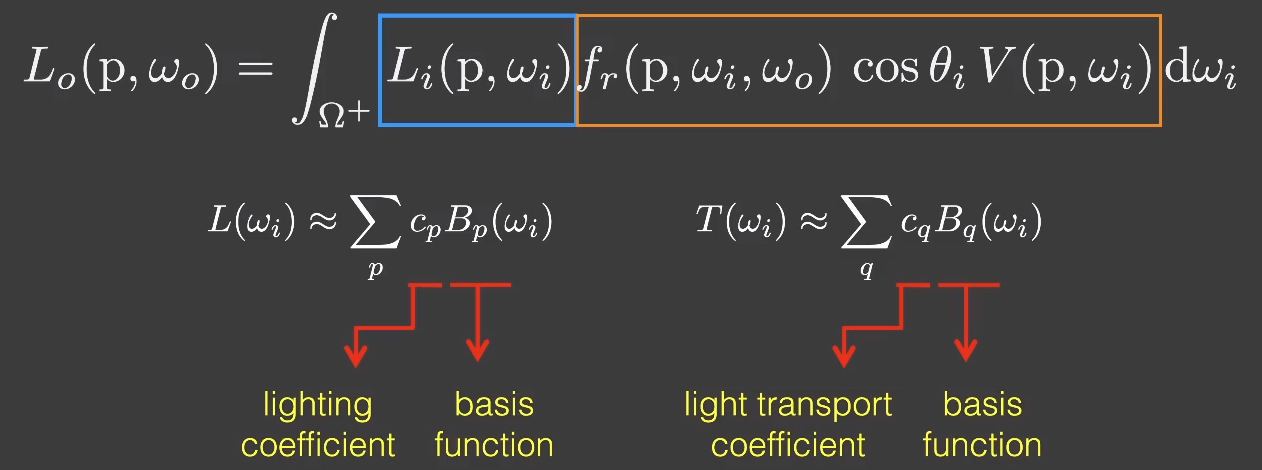
方程里的 和「基函数系数」提出来得到如下结果
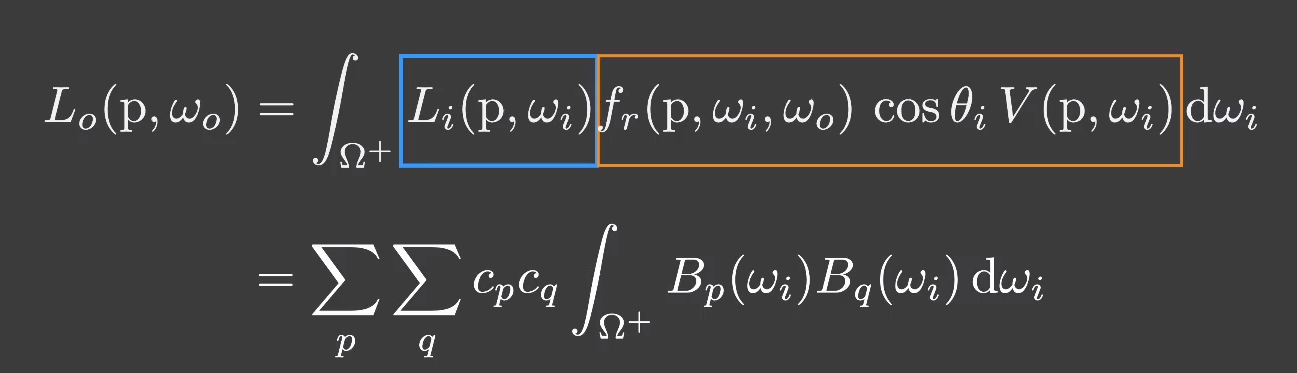
这个函数看上去像是一个 阶的(这里一般情况下 p 和 q 阶数可以视为相同),和之前的推到有冲突(之前结果是 i 阶),但实际上由于基函数的「正交性」,在基函数 上投影基函数 结果要不为 0,那么只能说明 。类似 的矩阵,只有对角线上值不为 0,计算得到的结果还是 p 或 q 阶 或者说 i 阶。
# Diffuse Rendering Results
计算方程内如果带上了「Visibility 函数」那么最终结果就会是有「shadow」的。

# Glossy BRDF Case
「Glossy BRDF」相比于「Diffuse BRDF」区别在于,不但要考虑入射角,还得考虑出射角,「Diffuse BRDF」的出射结果和出射方向关系不大,任意方向结果一致。但是「Glossy BRDF」针对不同的出射方向结果可能相差甚远。因此「Diffuse BRDF」的方程针对不同的入射角得到的是一个确定的结果,而「Glossy BRDF」针对不过的入射角,得到的是一个和出射角有关的方程。
这里再对 进行基函数展开,就可以得到一个和入射角和出射角有关的基函数方程:
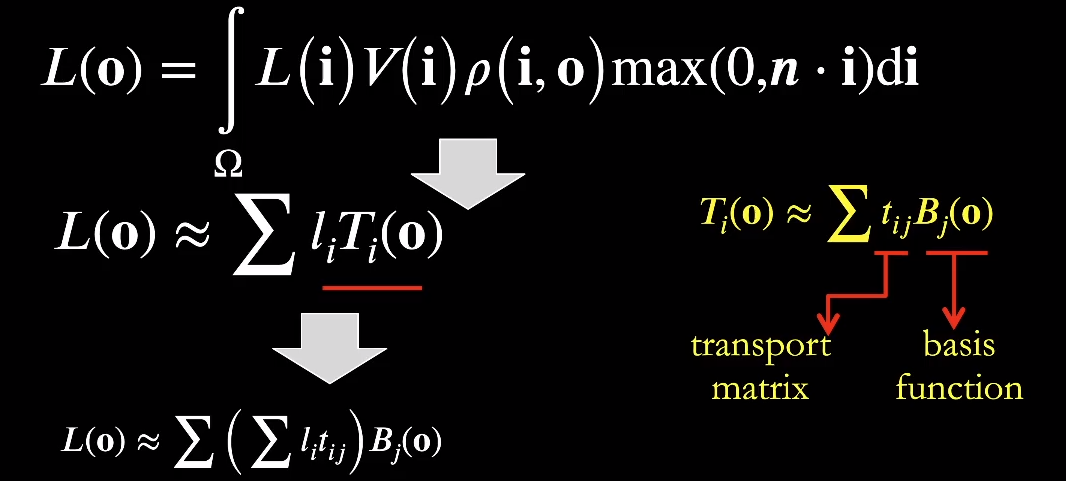
因此,「light transport」的预处理结果会是一个二维的贴图,横轴和纵轴分别表示「出射角」和「入射角」。
计算公式 。就是对一个一维向量和一个二维矩阵做乘积,最终结果是一个和「出射角」有关的一维向量。已知「入射角」然后根据不同的「出射角」进行查询,就可以得到对应的结果。

# Glossy Rendering Results

# Time Complexity
- 「SH」 Basis:9 / 16 / 25。diffuse 情况下一般 3 阶(9)足够,glossy 情况下 4 阶(16)和 5 阶(25)都有。
- Diffuse Rendering(以 16 个基函数为例)
- 任意位置的计算:
- Glossy Rendering(以 16 个基函数为例)
- 任意位置的计算:
# Precomputation
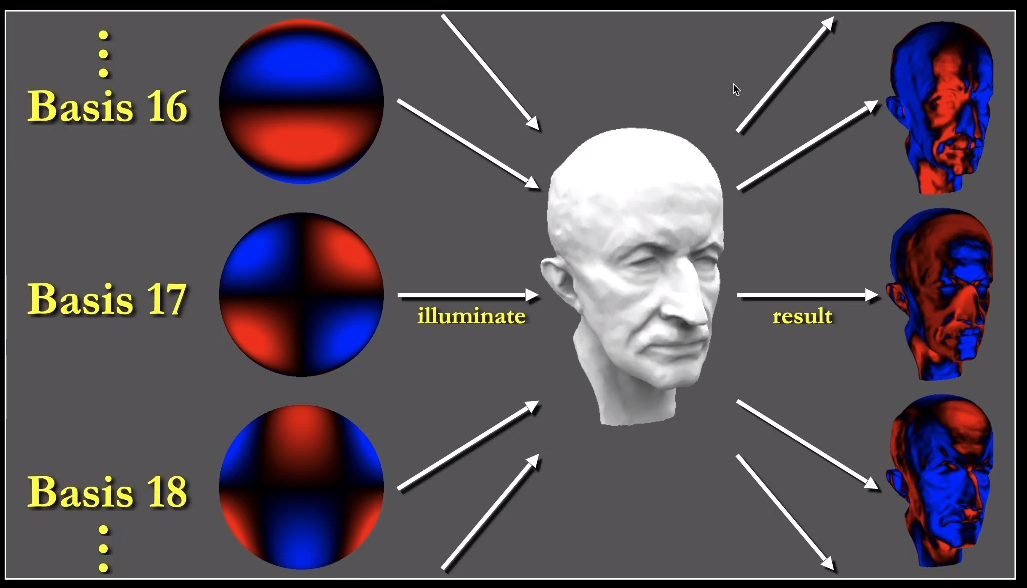
对于「基函数系数」的另一种理解是:
用「基函数 」作为「光照函数 」对一个物体的各个「shading point」进行计算,最终得到的贴图。
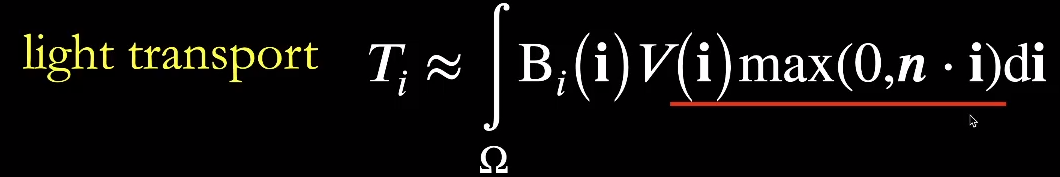
# Limitations
- Low-frequency
- 由于「SH」本身性质,导致其处理的频阶有限,虽然可以无限展开,但实际情况下不能这么处理。
- Dynamic lighting, but static scene/material
- 改变场景或者 BRDF 会使得之前的预处理结果失效,需要重新计算。
- Big precomputation data
# More basis functions
- Spherical Harmonics(SH)
- Wavelet
- Zonal Harmonics
- Spherical Gaussian(SG)
- Piecewise Constant
# Wavelet
2D Haar wavelet
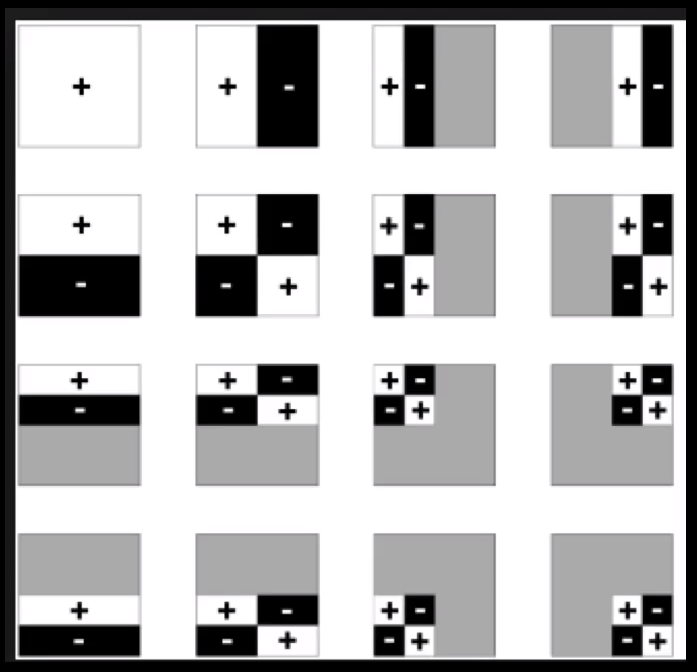
- A non-linear approximation:给定任何二维的函数,都可以投影到 wavelet 基函数上,并得到基函数系数。因此,可以保留其中系数较大的基函数。
- All-frequency representation:由于可以对任意二维函数进行投影,因此可以覆盖所有频率的函数 —— 高频 or 低频。
# wavelet transform
把一个二维函数描述成一个「cube map」,并对这张「cube map」进行 wavelet transform。
「wavelet transform」会把图中每个块分成四份,其中左上角保留低频数据,其他三个角记录高频数据。

依次类推,直到达到一个满意的精度。这样就既能够保留高频信息,又可以不增加存储量的得到基函数系数。

渲染出的结果可以支持低频和高频,但由于「Wavelet」没有「SH」的旋转特性,因此缺点是不支持对光源的旋转。
