以下为个人学习笔记整理,涉及坐标内容统一用右手坐标系,课程官网。
# Triangles
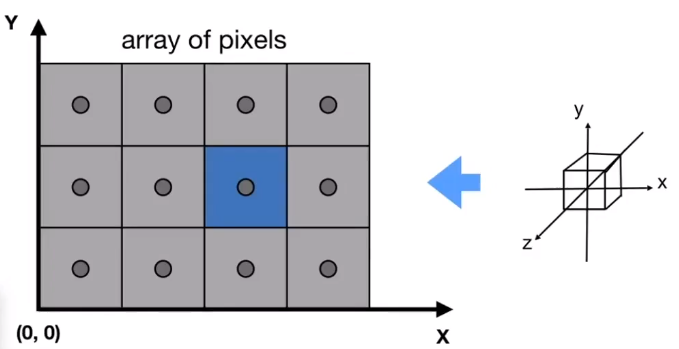
光栅化(Rasterization)其实是一种将几何图元变为二维图像的过程。
![image-20210102200504384]()
三维的[−1,1]3 的正方体转化为长为 witdh,宽为 height 的二位屏幕时,暂时先不考虑 Z 轴的情况下:
把 [−1,1]2 的坐标范围转换成 [0,2]2 的坐标范围
再拉伸成 [0,width]×[0,height]
视口变换:Mviewport=⎝⎜⎜⎜⎛2width00002height0000102width2height01⎠⎟⎟⎟⎞
# 为什么选择三角形作为图元
- 三角形是最基础的多边形。
- 任何其他不同的多边形都可以用三角形表示。
- 三角形的三个点都会在同一平面。
- 三角形的内外比较清晰(凸多边形和凹多边形比较困难)。
- 给定三角形的三个顶点,做插值比较方便(实现渐变)。
# 简单的光栅化
# 采用法
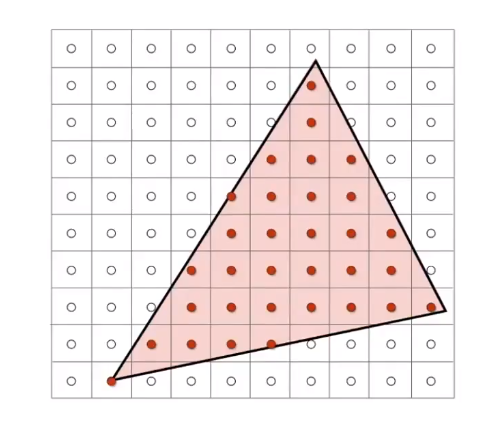
通过判断像素的中心是否在三角形内,来决定其颜色。
![image-20210102203025798]()
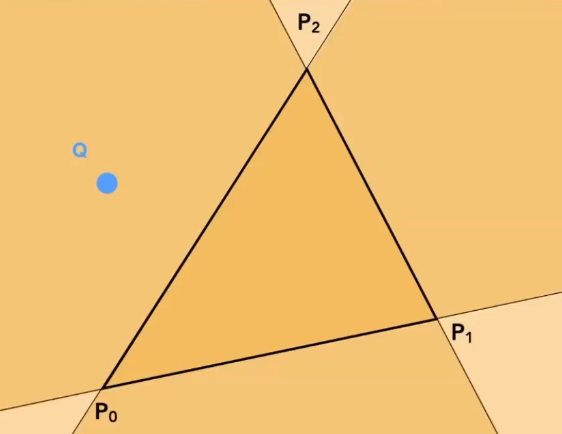
# 如何判断点是否在三角形内
只要三角形三条边和该点的叉积值的 z 方向都相同
P0P1×P0Q==P1P2×P1Q==P2P0×P2Q
![image-20210102203654335]()
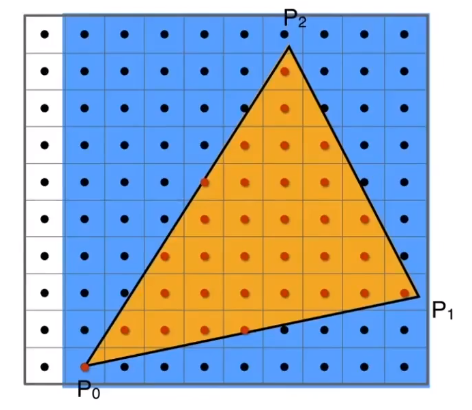
# 是否需要判断所有的点❓
不需要,只需要判断三角形包围盒(Bounding Box)范围内的像素
![image-20210102204115669]()
# 关键字
- 包围盒:二维坐标下,图像的 x 和 y 的取值范围所组成的矩形,被称为包围盒。三维坐标下类似。简称 AABB