# 光线追踪（Ray Tracing）

光线追踪主要是用来处理以下情况：

• 实现软阴影

• 处理光线需要多次弹射的时候

# Ray Tracing VS Rasterization

# Rasterization

• 实时计算。
• 光线质量较低。
• 计算量较小。

# Ray Tracing

• 离线的计算。
• 光线质量较高。
• 计算量巨大，耗时较长。

# Light Rays

为了方便计算，对于光线，有以下三个假设：

• 认为光是延直线传播
• 光线之间的传播不会收到其他光线影响。
• 光线经过一系列的传播之后，最终会进入人眼。

# 如何实现光线追踪💡

# 产生眼睛射线（Generating Eye Rays）👁‍🗨

产生眼睛射线有以下几个前提：

• 光线经过反射或折射后不会有损耗。
• 眼睛视作针孔摄像机（一个点）

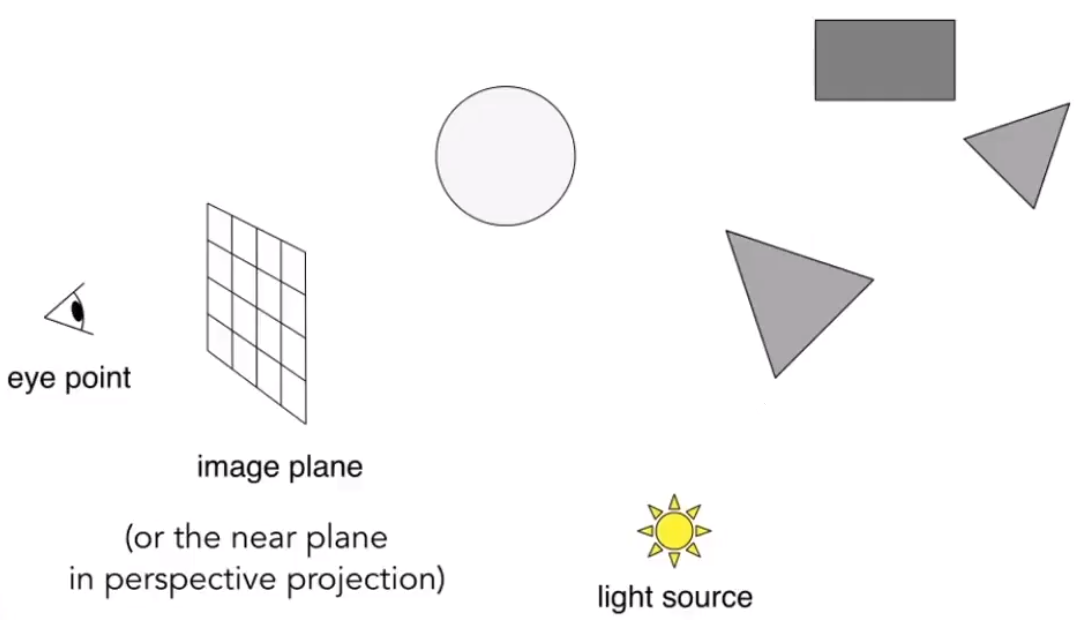
# 得到人眼能够观察到的点👀

沿着人眼，发射光线，会和场景内的物体产生交点，这里只记录最近的交点。

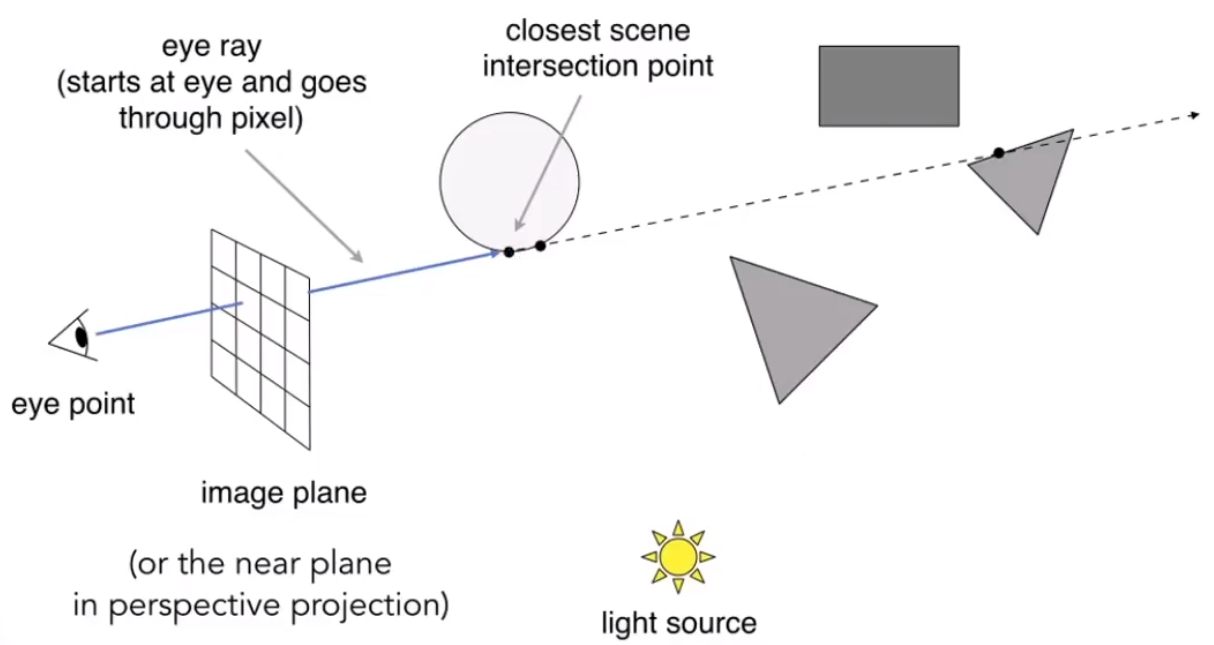
# 判断该点能否被光源照亮☀️

从交点连一条线到光源，如果中间没有物体遮挡，那么该物体就可以被人眼看见。之后就可以根据该点的法线和光源计算投影像素的着色。

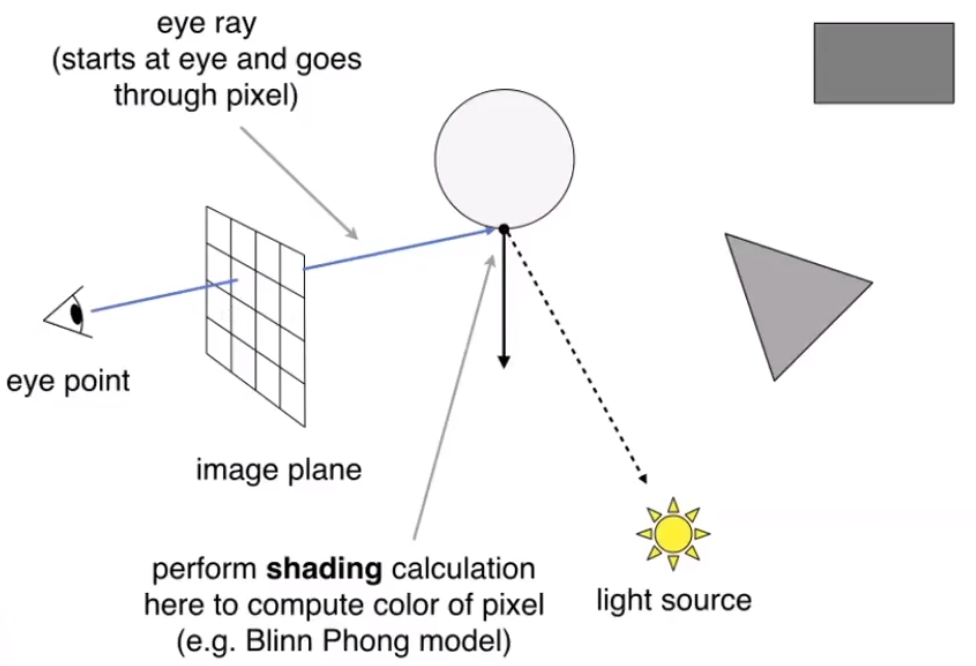
# 递归光线追踪（Recursive Ray Tracing）

考虑光线的「反射」和「折射」

• 人眼发射的光线再遇到物体时，一部分光线会发生反射，一部分光线会发生折射。
• 最终一条光线经过「反射」和「折射」再不同的物体上产生交点。
• 计算所有物体的交点和光源的关系，并根据每个点的光线权重，把最终值累加起来，就代表该点的像素。

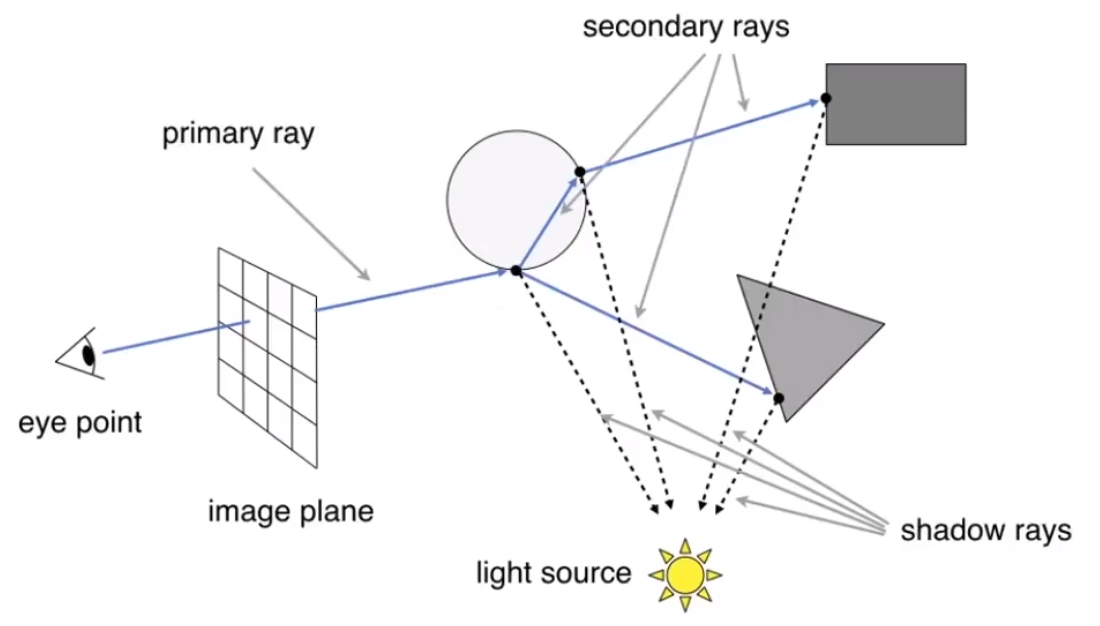
• Primary Ray：从人眼射出的未经过反射和折射的光线

• Secondary Rays：经过反射和折射的光线

• Shadow Rays：从物体连向光源的连线

# Ray-Surface Intersection

# Ray Equation

假定光线是一个起点和一个方向向量。

$$\text{光线的公式 Ray：} r(t) = o + td \quad \quad 0 ≤ t ≤ \infty$$

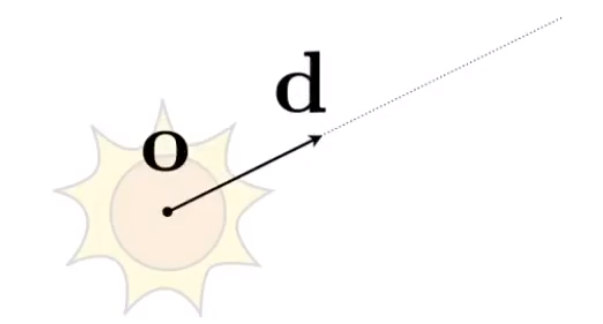
# 计算光线和其他物体的交点

# 光线和球的交点⚪️

就是计算，光线上的某个点也在球上。

$$\text{球的公式 Sphere} \quad p:(p-c)^2 - R^2 = 0$$

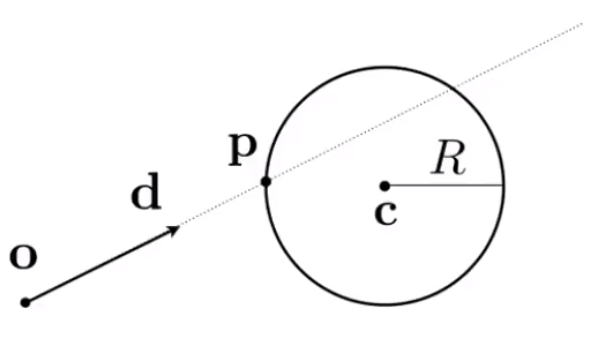
通过光线的公式和球的公式，可以得到一个计算交点的公式（$o,d,c,R$ 都已知）：

$$(o + td - c)^2 - R^2 = 0 \quad \to \quad at^2 + bt + c = 0$$

$$a = d \cdot d , \quad b = 2(o - c) \cdot d , \quad c = (o - c) \cdot (o - c) - R^2$$

$$t = \frac{ -b ± \sqrt{b^2 - 4ac}}{2a}$$

根据最后的 t 值得出交点。

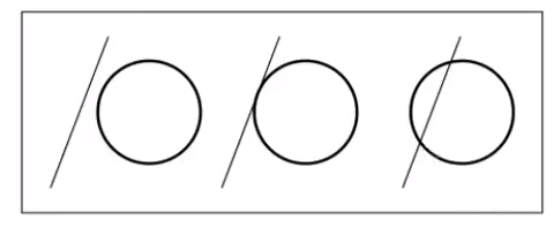
# 光线和任何物体的交点（隐式的表示）

假定任何物体都可以由 $p: f(p) = 0$ 的隐式公式来表示。

光线的表示：$f(o + td) = 0$ 。

那么所有的物体都可以通过上述球圆的规则进行求解。

# 光线和任何物体的交点（显式的表示）

显示的表示实际上就是光线和多个三角形面片组成的模型求交点。换而言之，就是计算光线和多个三角形如何求交。

计算光线和三角形求交又可以简单的进行分解：

• 光线和三角形所在的平面求交。
• 交点是否在三角形内。

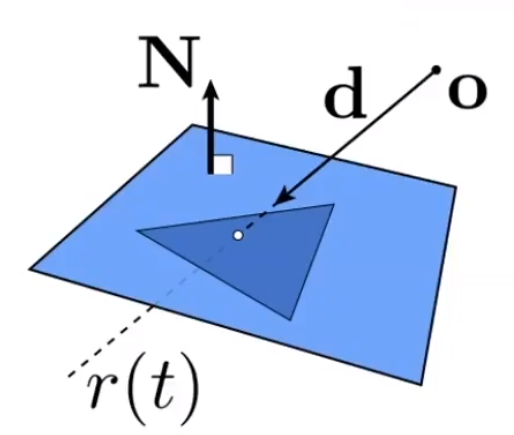
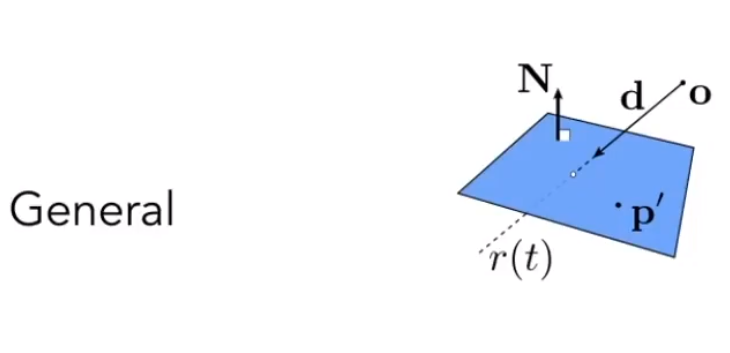
# 光线和三角形所在的平面求交

首先需要定义一个平面，定义平面可以理解为定义一个「点」和一个「法线」；点确定位置，法线确定方向。

所以平面上任意一个点都会满足如下性质：

• 该点和 $p^\prime$ 组成的向量必定和法线垂直。 $p:(p-p^{\prime}) \cdot N = 0 \quad \text{各点用坐标代替，最终公式} \to ax+by+cz+d = 0$

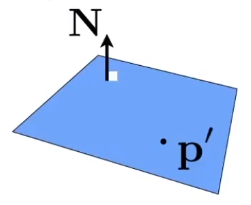
所以根据上述公式就可以计算两者的交点：

$$(p-p^{\prime}) \cdot N = (o+td-p^{\prime}) \cdot N = 0$$

$$t = \frac{(p^{\prime} - o) \cdot N}{d \cdot \N} \quad 0≤t≤\infty$$

# 交点是否在三角形内

参考第四课的内容，点和三角形各个点形成的向量求叉积。

# Moller Trumbore Algorithm

该算法可以直接计算三角形和射线的交点。三角形内的点，可以通过重心坐标表示，参考第九课。

$$\vec o + t \vec d = (1 - b_1 - b_2) \vec P_0 + b_1 \vec P_1 + b_2 \vec P_2$$

# Accelerating Ray-Surface Intersection

上述的方法虽然可以计算某个光线经过一系列反射折射，最终成像的结果，但是太慢了。如何加快速度呢？

# 包围盒（Bounding Volumes）

如果光线和物体的包围盒都没有交集，那么更不可能和物体之间有交点。

# Axis-Aligned Bounding Box（AABB）—— 轴对齐包围盒

轴对齐包围盒可以理解为「三对互相平行的平面」组成的「立方体」。

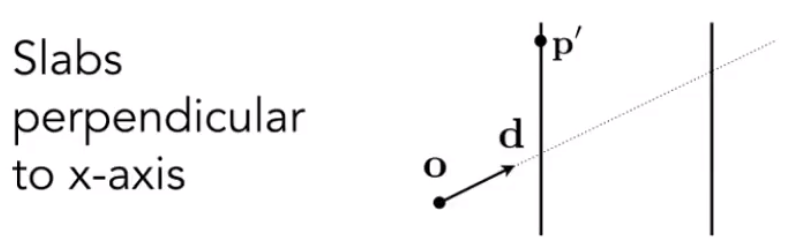
# 光线和包围盒求交

先考虑二维平面下，可以很容易计算出光线进入 $t_{min}$ 和离开 $t_{max}$ 每个两个平面的时间。

得到的两个 $t_{min}$ ，和两个 $t_{max}$。最终计算出 $t_{enter} = max(t_{min})$，$t_{exit} = min(t_{max})$

三维情况下类似。

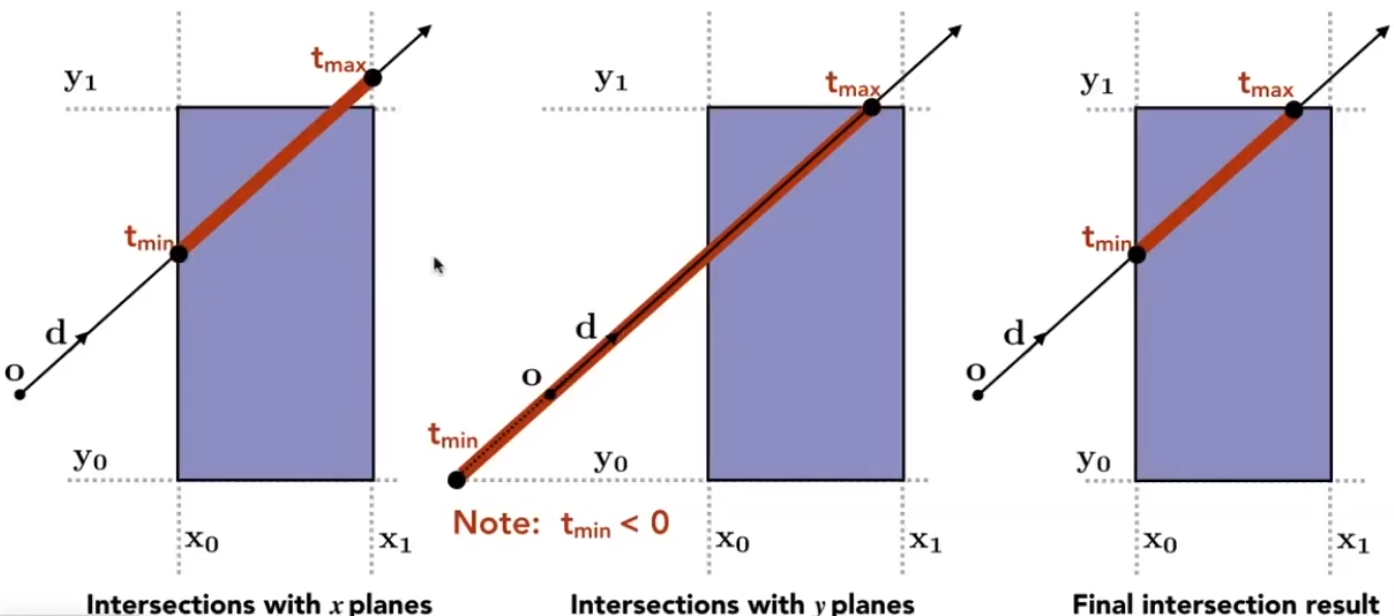
# 当 $t_{exit} < 0$ 时，表示光线在包围盒后面，不相交。

# 当 $t_{exit} >= 0, t_{enter} < 0$ 时，表示光线在包围盒内，相交。

有相交的情况，结论： $t_{enter} < t_{exit} \quad \& \& \quad t_{exit} >= 0$

# 简化后计算量对比

# 正常情况（3 减、6 乘、1 除）：

$$t = \frac{(p^{\prime} -o) \cdot N}{d \cdot N}$$

# 简化后的情况（1 减、1 除）：

$$t = \frac {p^{\prime}_x - o_x}{d_x}$$