以下为个人学习笔记整理,涉及坐标内容统一用右手坐标系,课程官网。
# Materials and Appearances
# 什么是材质(materials)
materials == BRDF
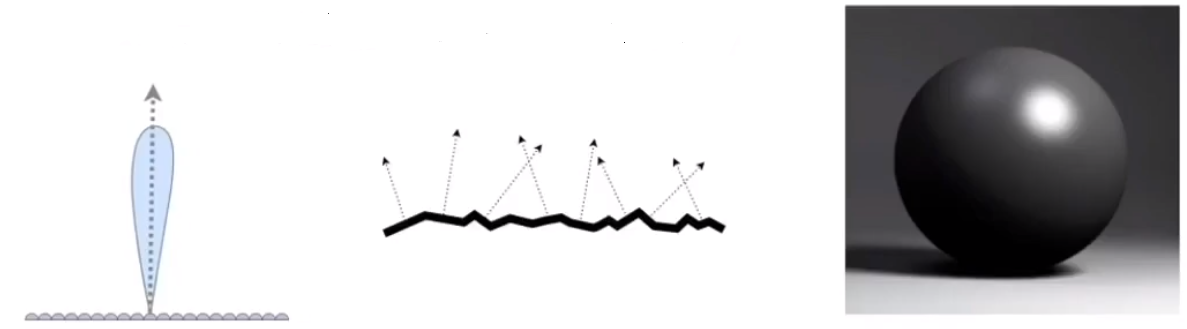
# 漫反射(Diffuse/Lambertian)材质
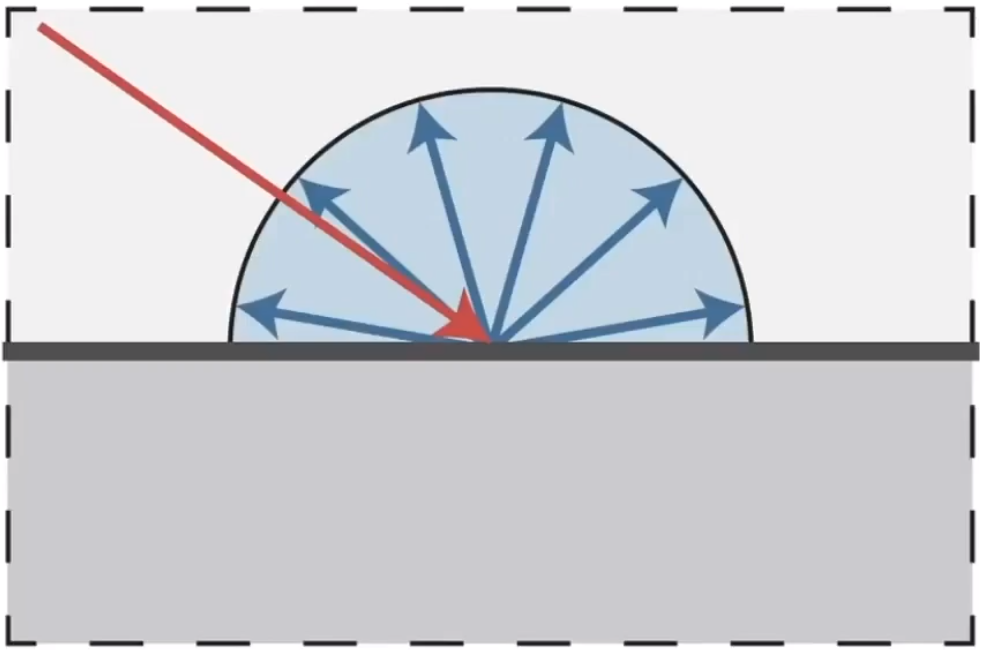
光线照射在某点后,均匀的分散到半球的各个方向。
![image-20210201101231275]()
由于能量守恒,假设物体本身不吸收任何光线,那么入射光的 「Irradiance」 将会等于出射光的 「Irradiance」。
![image-20210201174622150]()
Lo(wo)=∫H2frLi(wi)cosθidwi
假设入射光Li是常数:Lo(wo)=frLi(wi)∫H2cosθidwi
由于球的立体度为 4π ,半球的立体度则为 2π。而半球的立体度可以表示为(参考十六课):
∫Ωsinθdω=∫02π∫02πsinθdω=2π
此处忽略计算步骤:∫H2cosθidwi=π
Lo(wo)=frLi(wi)π
由于入射Li等于出射Lo,所以漫反射的BRDF:fr=π1
# 光滑(Glossy)的材质
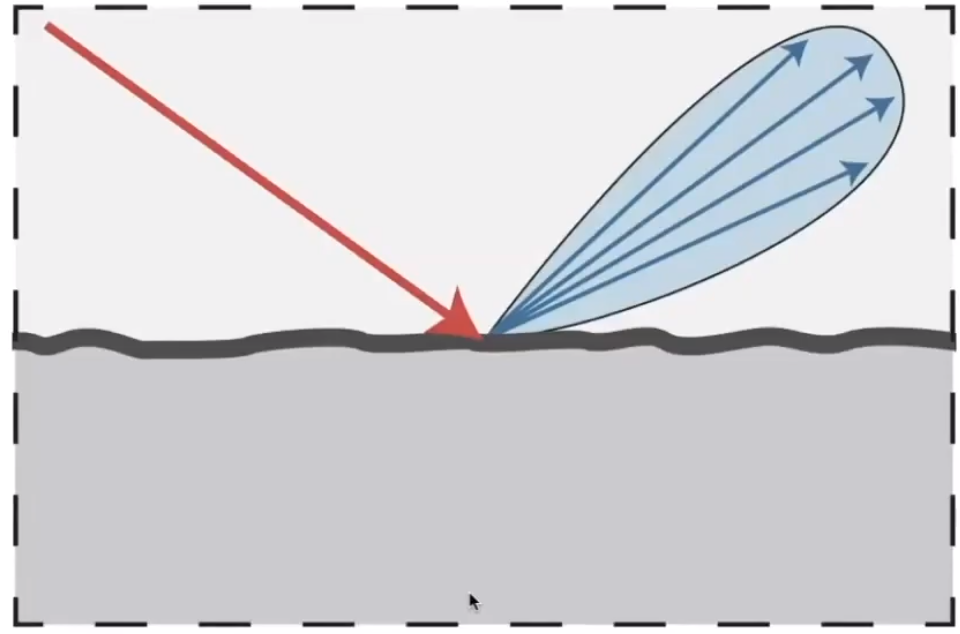
效果看上去有点像金属。
![image-20210201105829086]()
一条入射光,能够在某片区域,反射出多个光线,称之为 「Glossy」。
![image-20210201105902123]()
# 理想反射 / 折射(Ideal reflective/refractive)材质
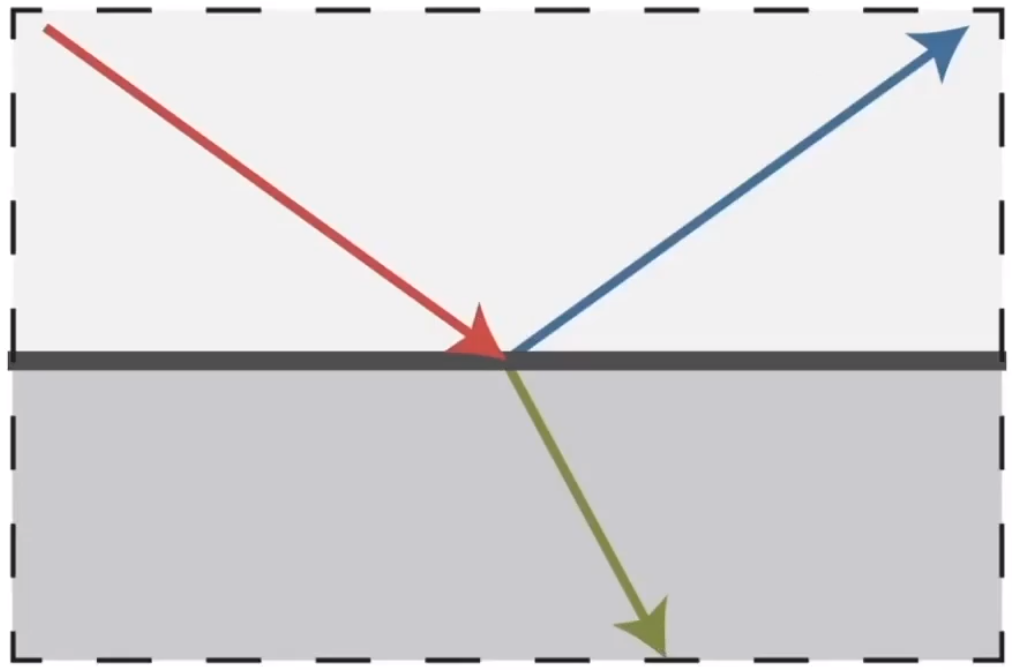
效果上来说,有点像玻璃和水。
![image-20210201110752169]()
光线通过物体进行反射和折射。
![image-20210201110451953]()
# 反射(Reflection)
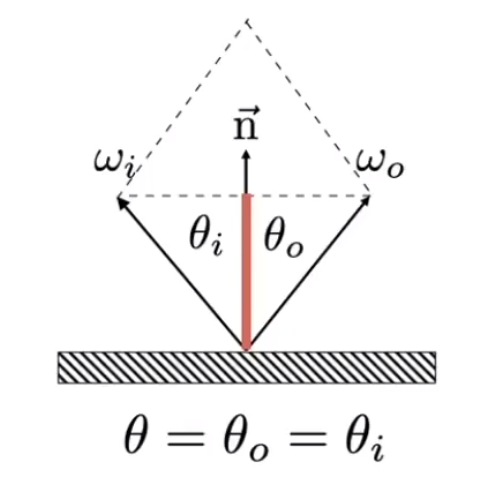
入射角等于出射角。
![image-20210201110932581]()
# 计算反射方向:
![image-20210201111135009]()
wi+wo=2cosθn=2(wi⋅n)n
wo=−wi+2(wi⋅n)n
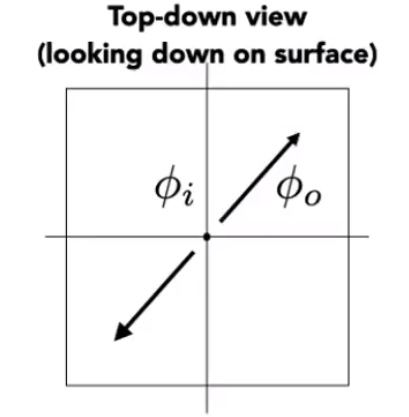
- 通过立体角的性质,假设从 z 轴向 z 轴负方向观察光线。
可以理解为入射角和反射角在 x,y 平面上旋转 180∘。
![image-20210201111707649]()
ϕo=(ϕi+π)mod2π
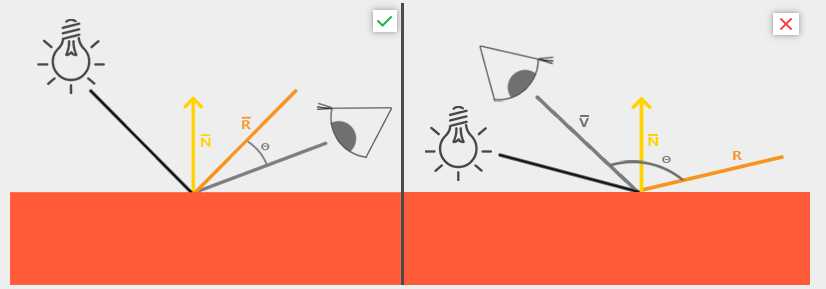
# difference between phong and blinn phong
「phong」模型考虑光线是用观察方向和反射方向做运算,在某些特定的情况下,这个角度会大于 90∘ ,而被抛弃。
![image-20210201114227159]()
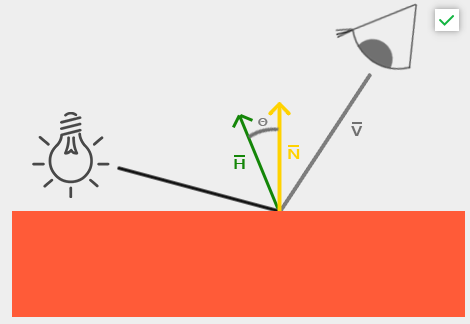
「blinn phong」模型则是直接用光源和观察方向的中间向量和法线之间的夹角来计算,该值不会被抛弃,而且计算效率也更高。
![image-20210201114353495]()
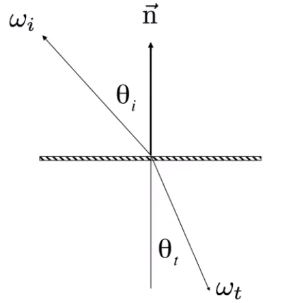
# 折射(Refraction)
![image-20210201115307355]()
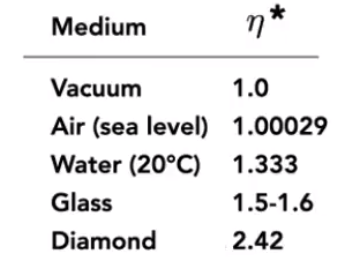
ηisinθi=ηtsinθt
![image-20210201140609854]()
转换为余弦:cosθt=(1−sin2θt)=1−(ηtηi)2sin2θi=1−(ηtηi)2(1−cos2θi)
发生折射的条件:ηtηi>1
折射和反射效果类似。
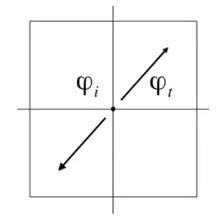
![image-20210201115527610]()
φt=φi±π
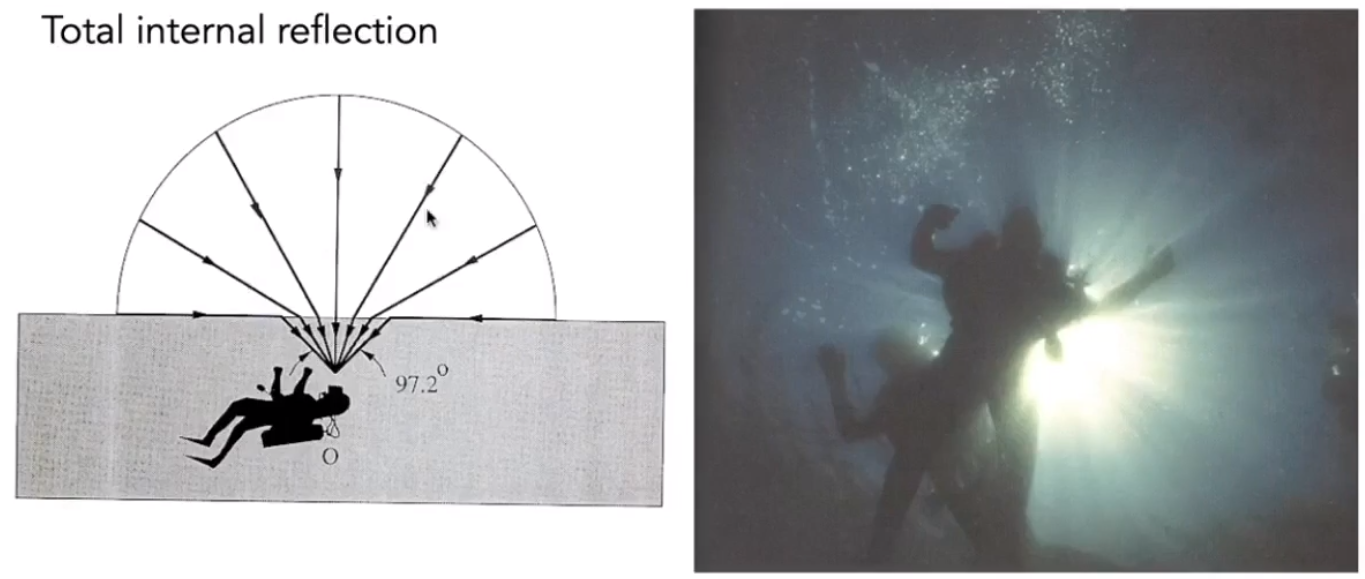
# Snell Window/Circle
在水底向上看的时候,只能看见较小的一块锥型区域。
![image-20210201141903830]()
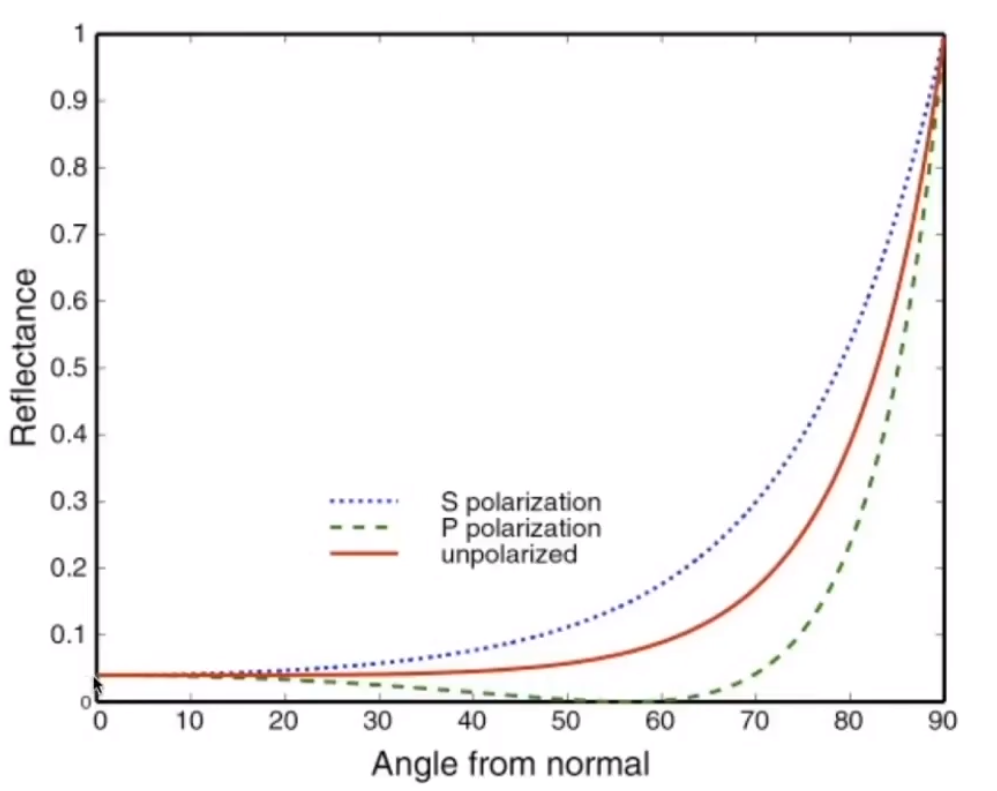
# Fresnel Reflection / Term
反射率会随着入射角的变化而变化
![image-20210201142658704]()
# Fresenel Term(Dielectric, η=1.5)
入射光线越是平行物体表面,反射率越大。越是垂直于表面,折射率越大。
![image-20210201142842883]()
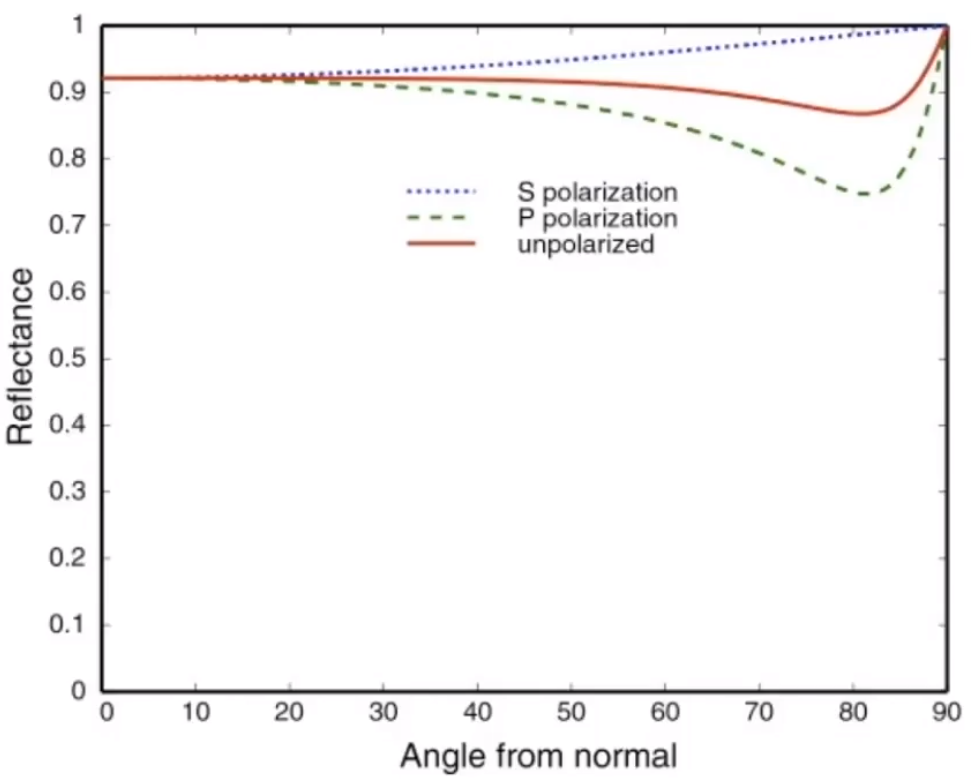
# Fresnel Term(Conductor)
导体(金属)在入射光和法线角度偏小的情况下依旧有着不错的反射能力。
![image-20210201143545593]()
对每个极化单独计算反射率,最终求平均。
Rs=∣∣∣∣∣n1cosθi+n2cosθtn1cosθi−n2cosθt∣∣∣∣∣2=∣∣∣∣∣∣∣n1cosθi+n21−(n2n1sinθi)2n1cosθi−n21−(n2n1sinθi)2∣∣∣∣∣∣∣2
Rp=∣∣∣∣∣n1cosθt+n2cosθin1cosθt−n2cosθi∣∣∣∣∣2=∣∣∣∣∣∣∣n11−(n2n1sinθi)2+n2cosθin11−(n2n1sinθi)2−n2cosθi∣∣∣∣∣∣∣2
Reff=21(Rs+Rp)
简化版计算方法(近似值)
R(θ)=R0+(1−R0)(1−cosθ)5
R0=(n1+n2n1−n2)2
# 微表面(Microfacet)材质
当观察点距离物体足够远的时候,很多物体表面的细节,无法观测到,只能看到光线对物体表面的一个总体作用。
理解成:光滑的物体虽然看上去表面光滑,但是用放大镜观察依旧能看到坑坑洼洼的地方,但最终的光照效果确实非常的光滑。
# Microfacet Theory
对于粗糙的物体表面
- 远处看:看到的是材质和外观。
- 近处看:看到的是几何。
![image-20210201151737332]()
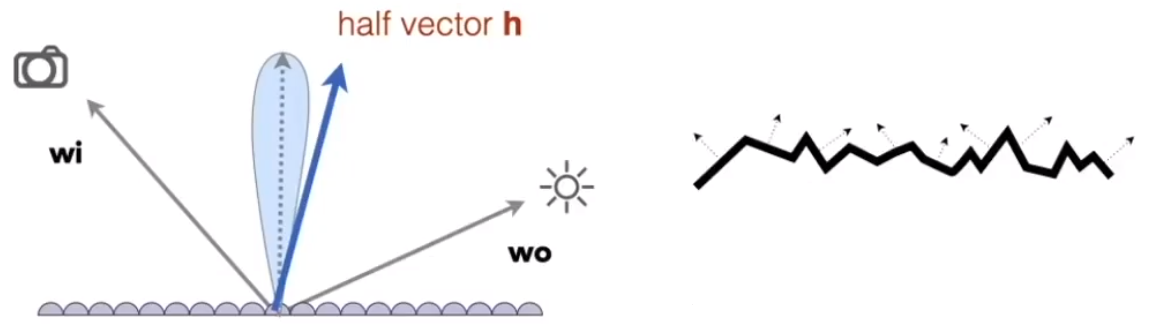
# Microfacet BRDF
微表面的法线分布:
- Concentrated < == > glossy
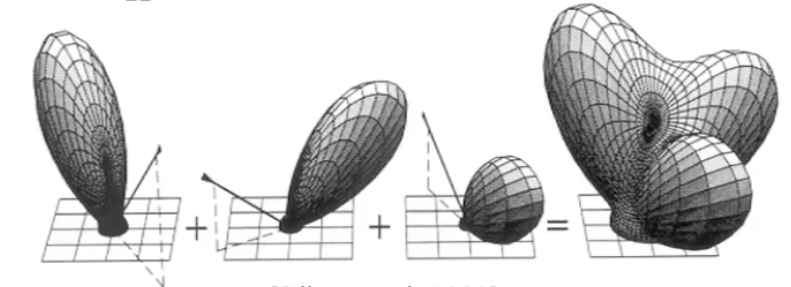
![image-20210201163305776]()
![image-20210201163213329]()
# 如何计算微表面的材质
![image-20210201164308639]()
f(i,o)=4(n,i)(n,o)F(i,h)G(i,o,h)D(h)
各个函数含义:
- F(i,h):Fresnel term,计算能够被反射的能量。
- G(i,o,h):shadowing-masking term,微表面之间是否存在互相遮挡。一般用于降低物体表面轮廓的亮度。
- D(h):distribution of normals,法线分布,表示任何方向的法线分布值。得到法线就能够判断光线是否会经过反射,进入人眼。
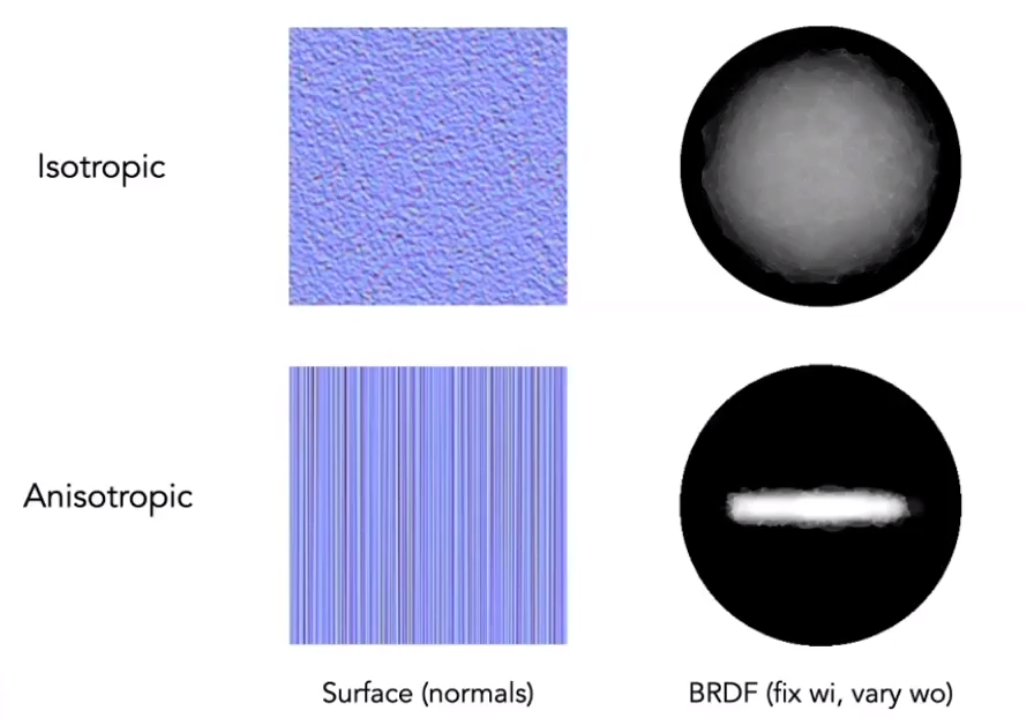
# Isotropic / Anisotropic Materials(BRDFs)
同向或异向的判断条件:沿着 z 轴方向旋转,各个立体角的「BRDF」是否相同(一个球体绕着 z 轴旋转,最终的观察结果是否不同)。
![image-20210201170225045]()
![image-20210201170352116]()
# Anisotropic Materials
在方位角旋转后,得到的 BRDF 不一致,那么就称之为「Anisotropic Materials」
fr(θi,ϕi;θr,ϕr)=fr(θi,ϕr;θr,ϕr−ϕi)
# BRDF 特性
- 非负:fr(wi→wr)≥0 。
- 线性性质:
Lr(p,wr)=∫H2fr(p,wi→wr)Li(p,wi)cosθidwi
![image-20210201171835282]()
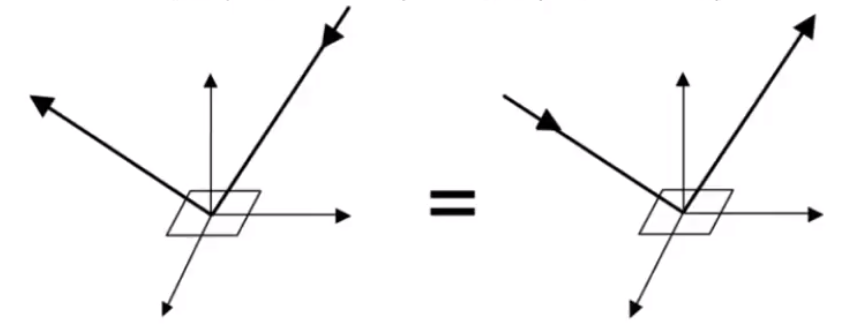
- 可逆性:fr(wr→wi)=fr(wi→wr)
![image-20210201171927569]()
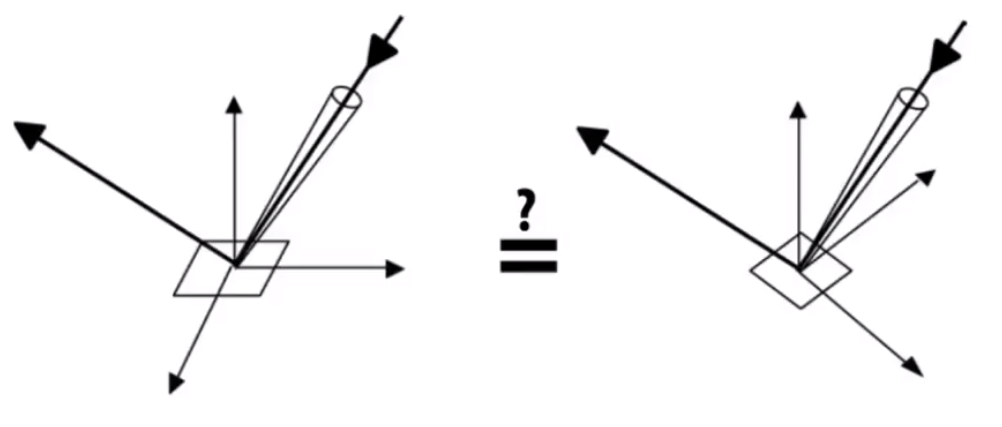
∀wr∫H2fr(wi→wr)cosθidwi≤1
- 各向同性 vs 各向异性
- 各向同性:fr(θi,ϕi;θr,ϕr)=fr(θi,ϕr;θr,∣ϕr−ϕi∣) 。
- 所有的 BRDF 都是可逆的。
![image-20210201173106066]()
# Measuring BRDFs
![image-20210201173421783]()
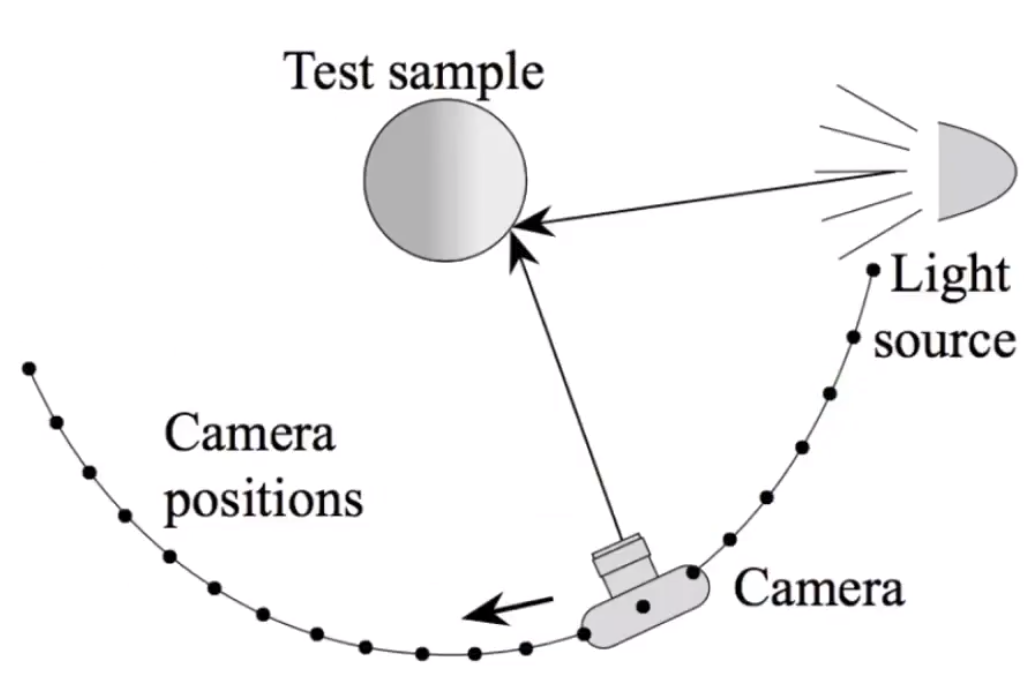
# gonioreflectometer
通过得到物体在不同位置光源和摄像机下的成像,计算出物体的 BRDF。
![image-20210201173748469]()
# 性能优化
- 假设材质是各向同性:较少一个维度的计算。
- 所有的 BRDF 都是可逆的,减少一半的计算量。
- ...
# 关键字
- Polarization(极化):波在多个方向上振荡的能力。
- MERL BRDF Database:各类 BRDF 的数据库。