# 光线追踪（Ray Tracing）

如何提高判断光线和物体是否有交点的速度呢❓

# 统一空间划分（Uniform Spatial Partitions）「Grids」

所有的空间划分，都是建立在计算光照之前。

适用于场景内物体分布均匀的情况。

# 预处理（Preprocess）

• 构建物体的包围盒。

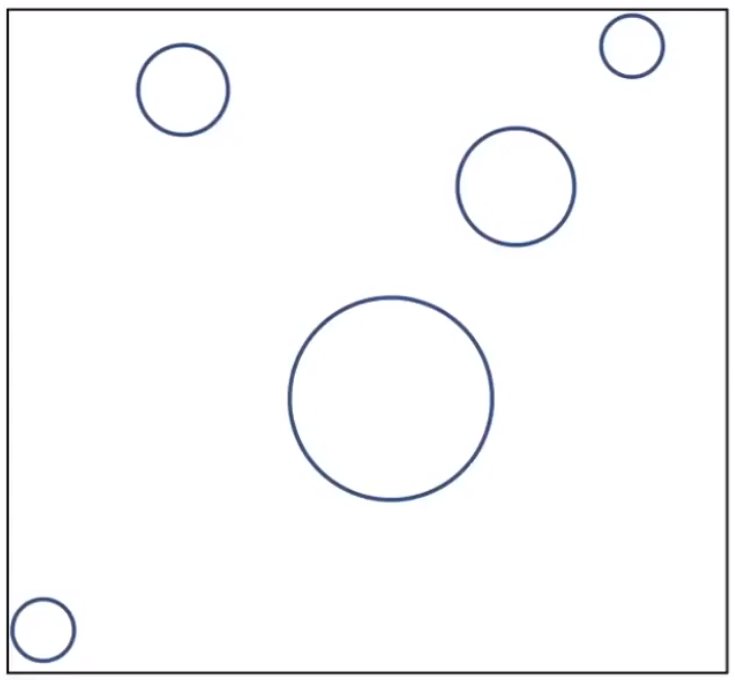
• 构建包围盒内的网格。

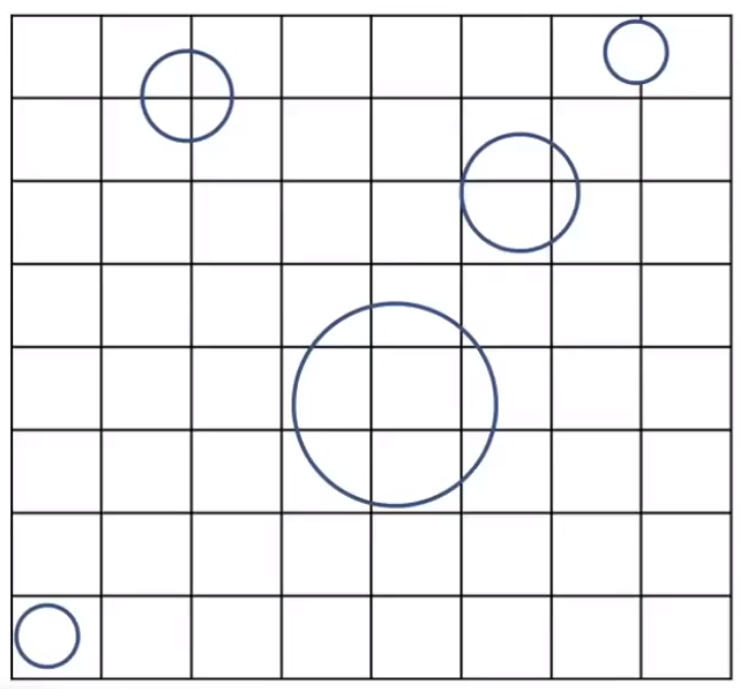
• 判断包围盒内是否有物体。

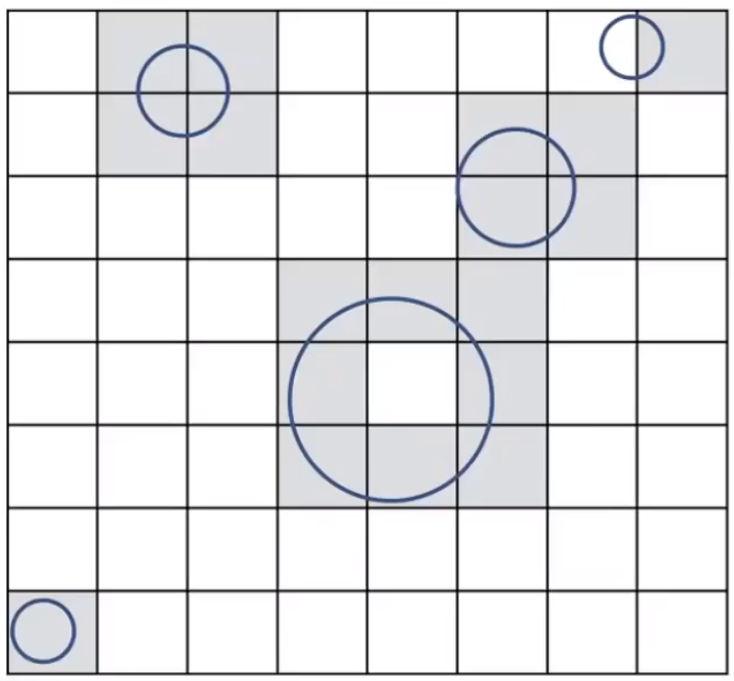
# Ray-Scene Intersection

假设：光线和实际物体求交的速度非常慢，但和网格求交非常快。

• 计算出和光线会发生相交的盒子。
• 判断盒子内是否存在物体。
• 存在的情况下，对光线和盒子内的物体求交点。

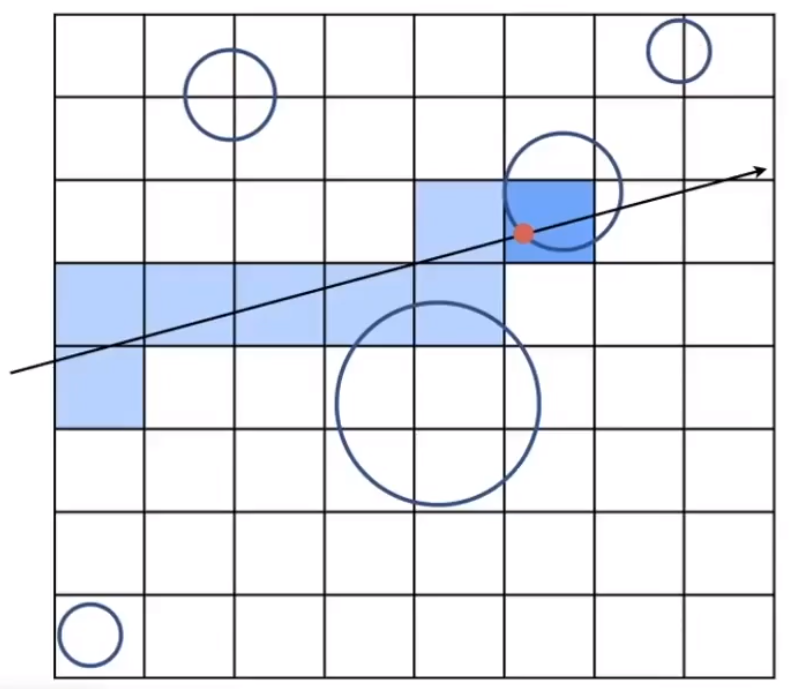
这里存在一个平衡，如果格子划分太大或者太小，都可能降低性能。

# 空间划分（Spatial Partitions）

相比于「Uniform Spatial Partitions」。「Spatial Partitions」针对不同大小的物体，会采用不同的划分方式，以减小计算消耗。

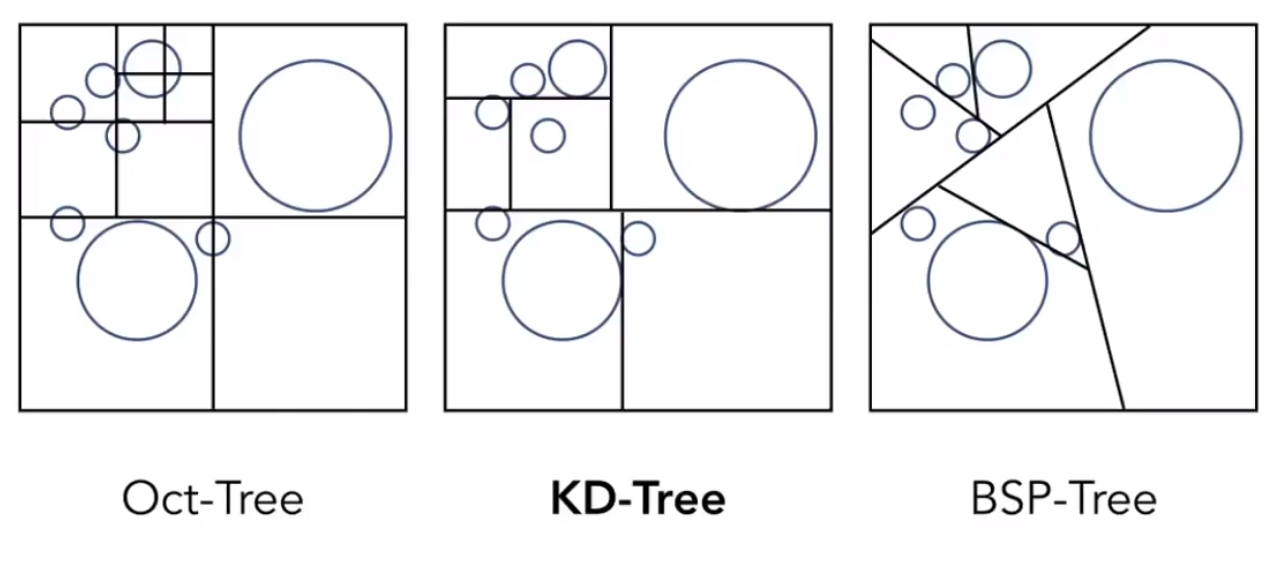
# 八叉树（Oct-Tree）

把空间的立方体切分为八块。再对新的八个方块进行类似操作，以此类推。二维空间内，就是四叉树。

# KD-Tree

相比于八叉树，直接对空间中的立方体砍三刀。「KD-Tree」每次只会沿着包围盒砍一刀（x 轴一下，y 轴一下，z 轴一下，保证空间均匀）。

这样整个结构就类似一个二叉树。

# KD-Tree Pre-Processing

先给空间竖的砍一刀。

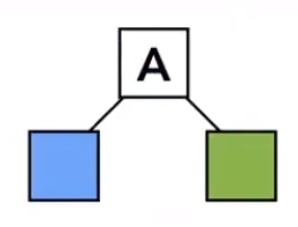
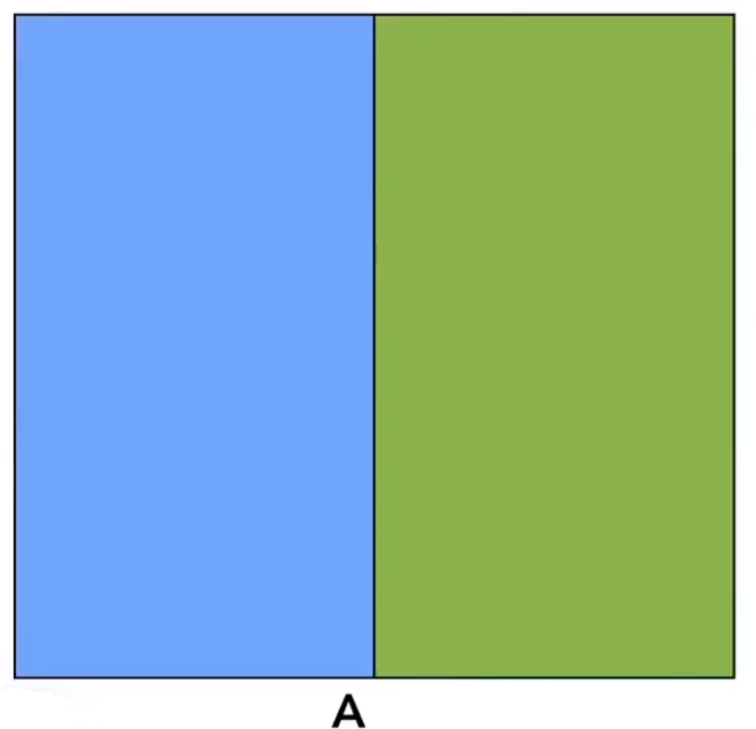
再对每个小空间，横的砍一刀（按理是需要继续划分的，这里只画一半）。

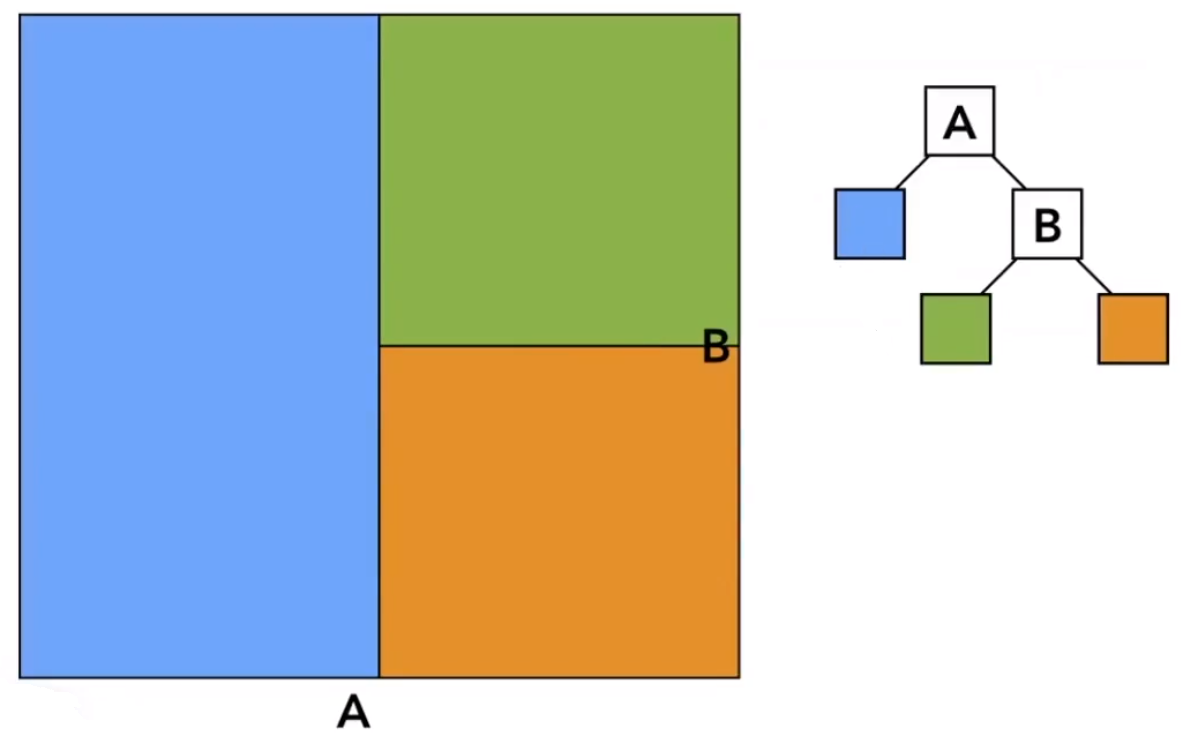
一直这样反复，最终可以得到一个二叉树结构，然后树的叶子节点就存储了该节点下的物体。

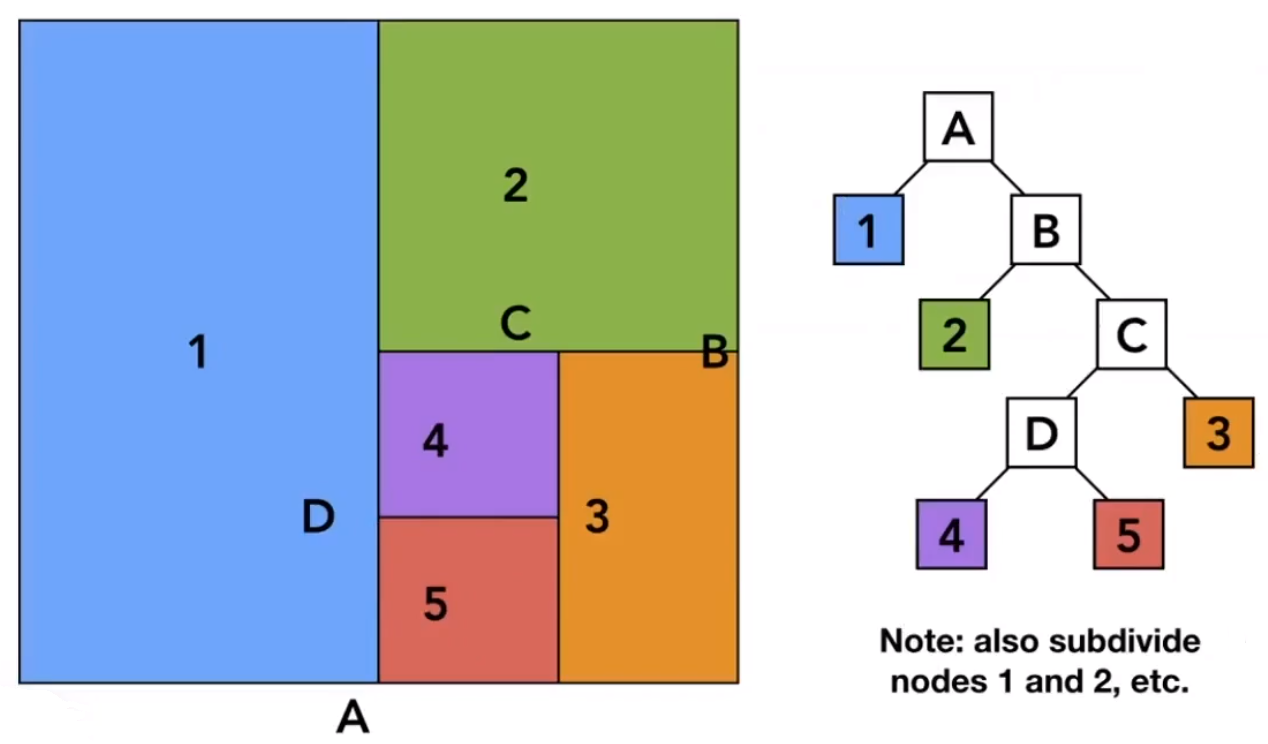
# Traversing a KD-Tree

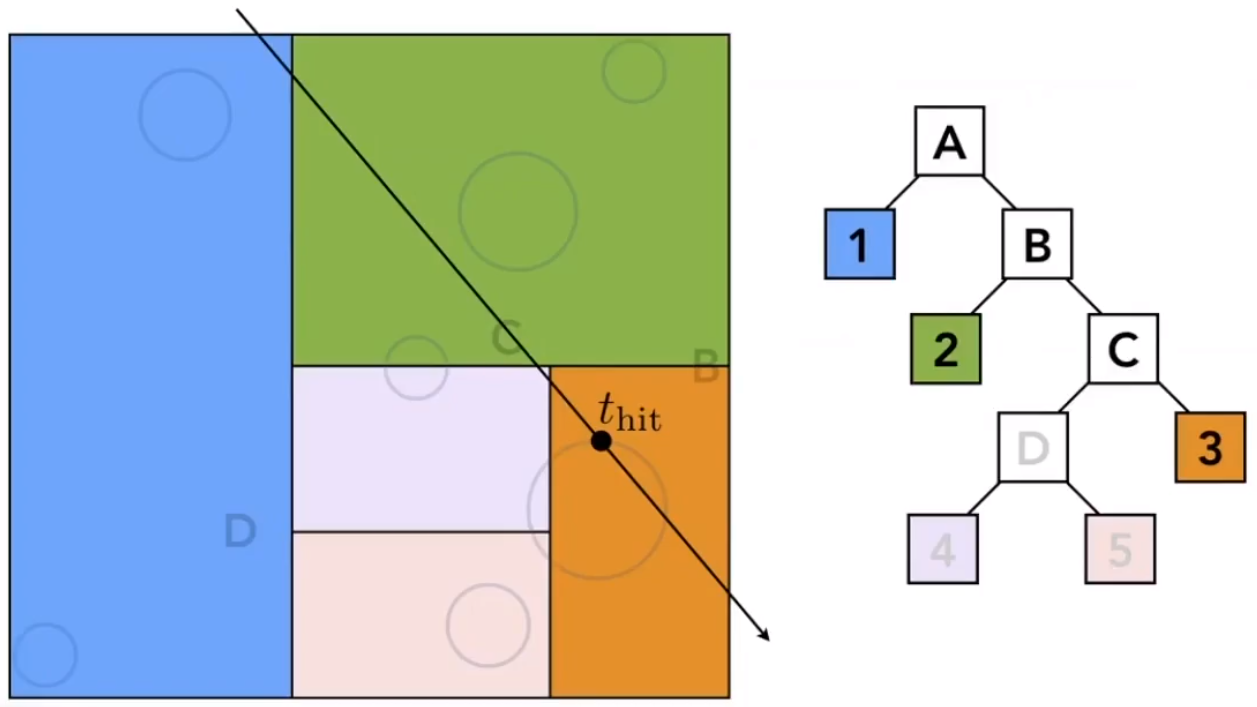
• 依次从根节点开始，遍历格子是否和光线有交点。

• 如果有交点，切该节点非叶子节点，则分别求其子节点是否和光线有交点。

• 之后就可以求得光线和所有有交点的叶子节点。

• 再把在叶子节点的所有物体都和光线求交，就可以判断哪些物体和光线存在交点了。

# 「KD-Tree」的弊端

• 很难判断一个三角形和一个物体是否相交（三角形三条边和物体之间都没相交的情况 —— 包裹了物体）。
• 如果一个物体同时存在多个盒子里，就需要对物体进行多次相交计算。

# BSP-Tree

类似「KD-Tree」，只不过砍的时候，是斜着砍的。

# Object Partitions & Bounding Volume Hierarchy（BVH）

相比于上面的针对空间的划分，该划分方式则是以「物体」为单位的划分。

# Bounding Volume Hierarchy（BVH）

首先把所有物体归到一个包围盒内。

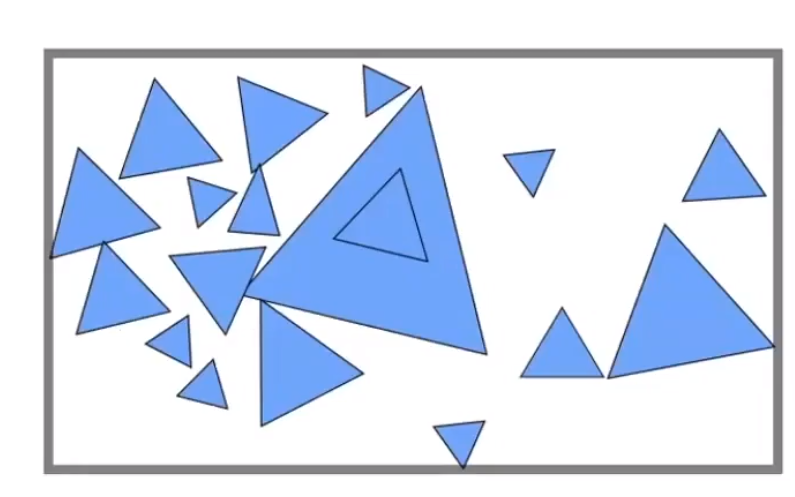
把当前的包围盒「试图」（暂不考虑怎么分）分为两部分。

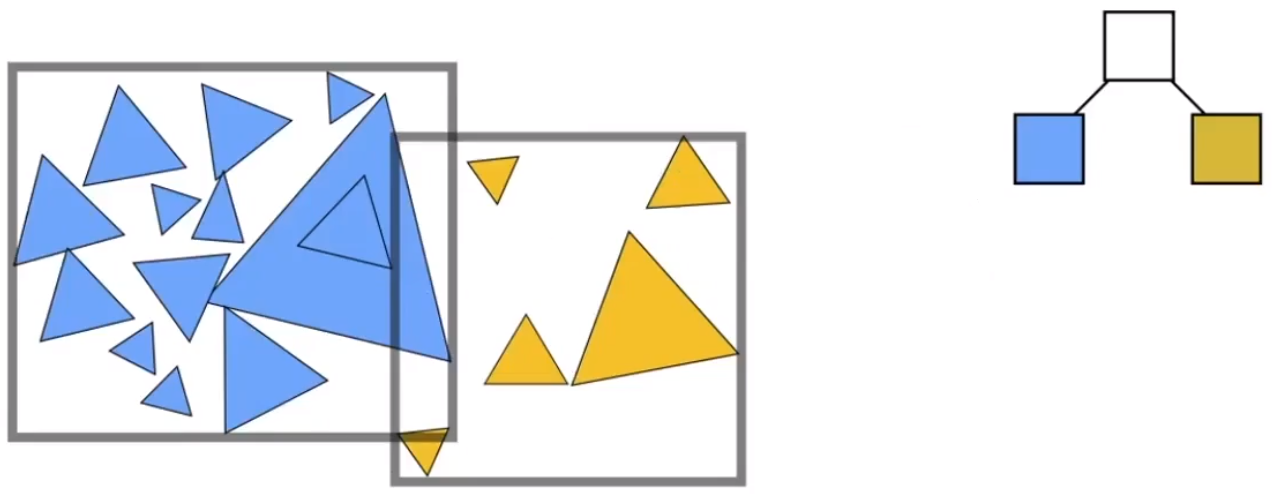
以此类推，继续划分，知道满足某些规则后停止。例如：某个盒子内有 N 个三角形。

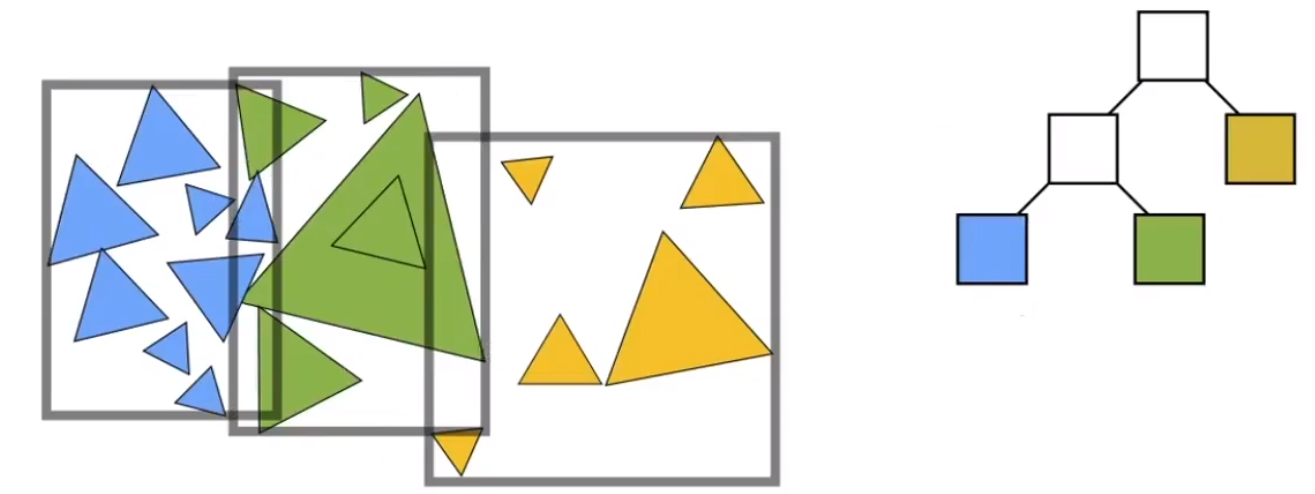
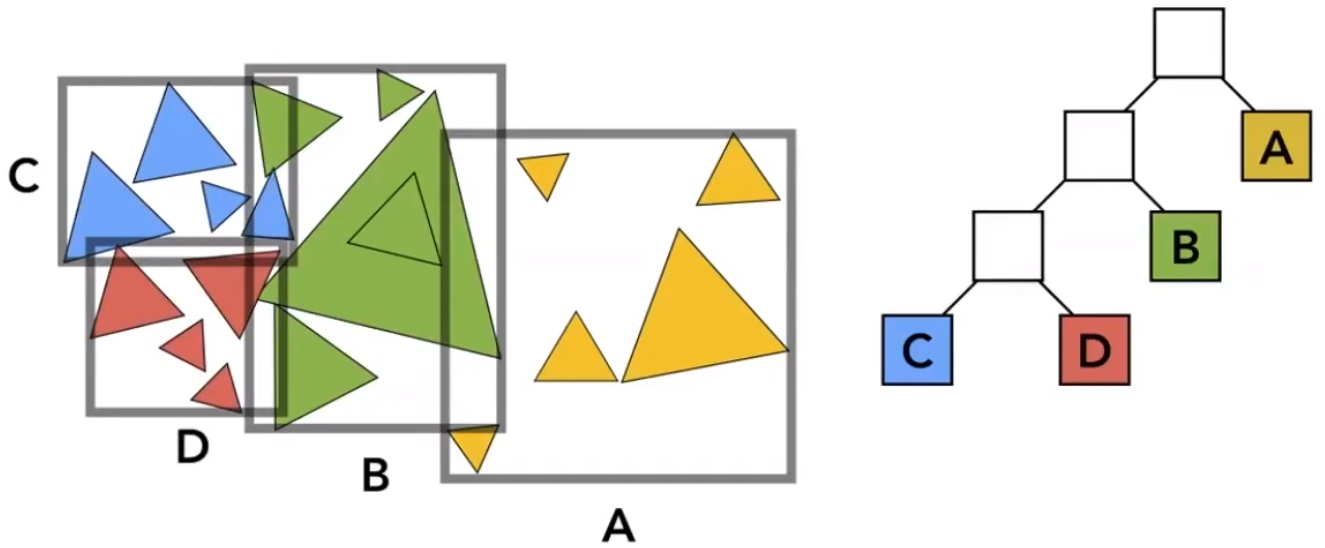
# BVH 的性质：

• 一个物体只能存在于一个盒子内。
• 不同的盒子之间会有交集。

# Building BVHs

划分包围盒的策略很多，例如：

• 每次都按照最长的轴进行划分（保证包围盒划分均匀）。
• 从包围盒中间的物体进行划分（保证两颗树保持平衡）。

# 扩展阅读

• GTC news：DLSS 2.0 传送门

• GTC news：RTXGI 传送门

# 关键字

• 快速选择算法：求 n 个数内，第 i 大的数。时间复杂度 $O(n)$。本质上就是快排，每次的锚点就是第 k 大的数，然后根据锚点 k 和 i，判断是否继续进行快排和快排的集合。