以下为个人学习笔记整理,涉及坐标内容统一用右手坐标系,课程官网。
# 曲面(Surfaces)

# 双三次贝塞尔曲面补片(Bicubic Bezier Surface Patch)
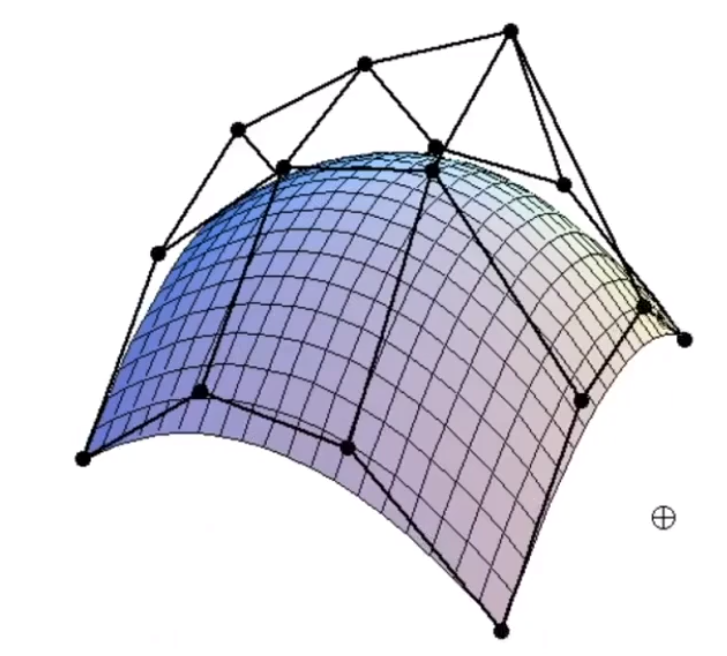
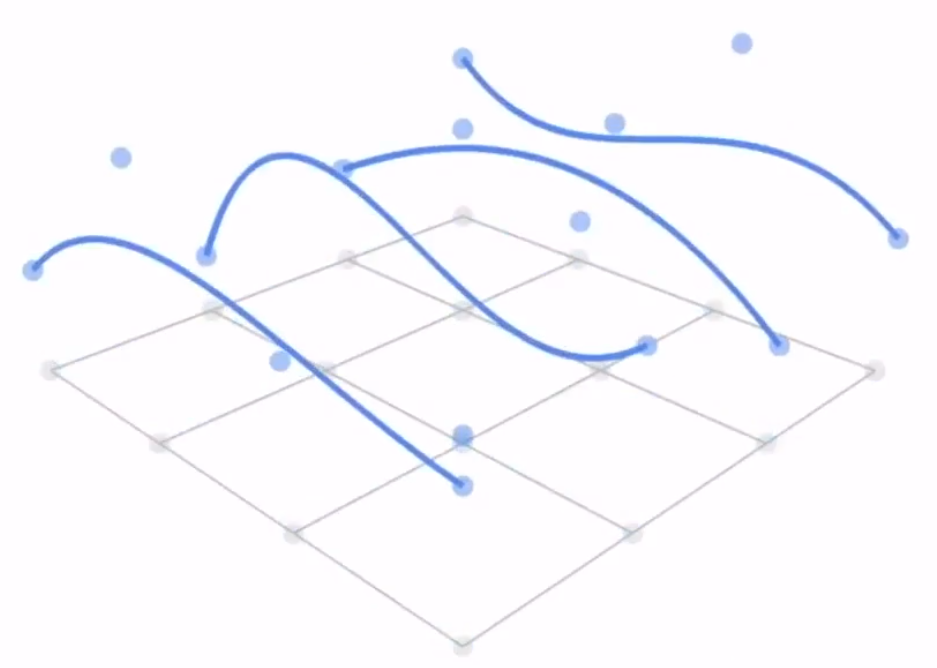
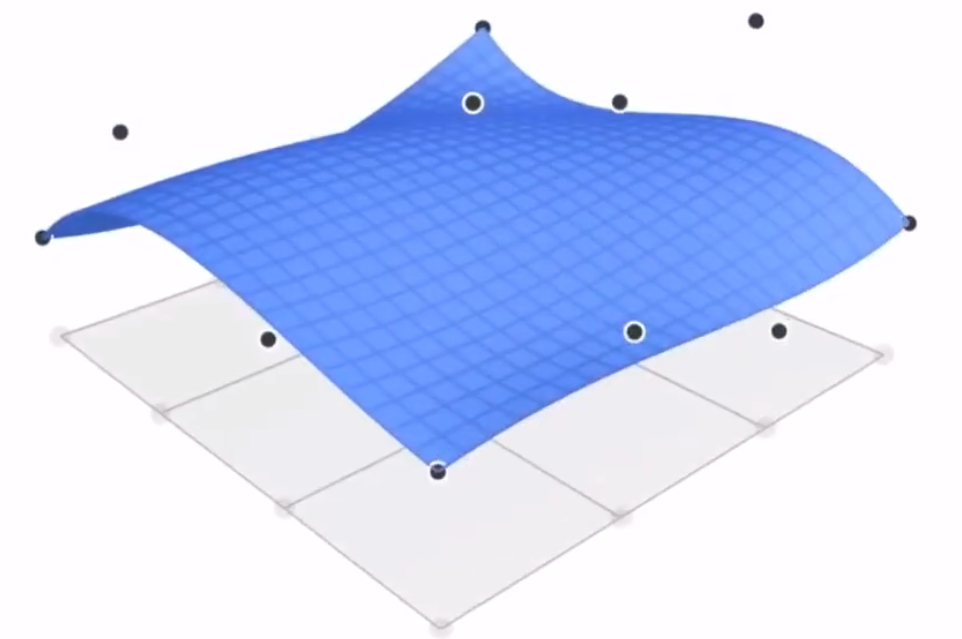
可以理解为通过 16 个控制点,得到 4 条贝塞尔曲线。

再通过 4 条贝塞尔曲线,得到一个贝塞尔曲面。
# 网格相关操作

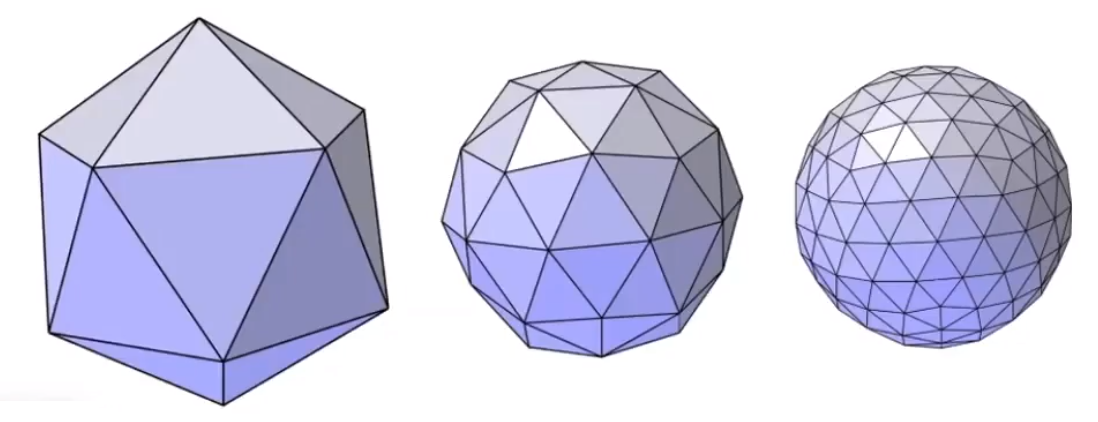
# 网格细分(Mesh subdivision)
把一个三角形拆分成多个小的三角形,并把拆分的三角形进行一定规则的移动。
# Loop Subdivision
# 「Loop Subdivision」细分操作的基本单元必须是三角形,不适用于非三角形的面片。
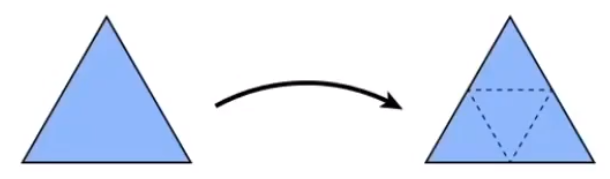
# 对原有的顶点和新得到的顶点进行不同规则的变换
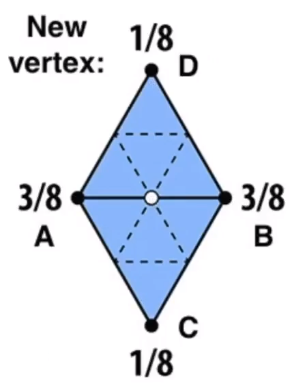
- 对于新的顶点:这里如果求「白色」顶点的位置。「A,B」是和白点共线的顶点;C,D 是和白点不共线的顶点。这里给出的计算公式如下
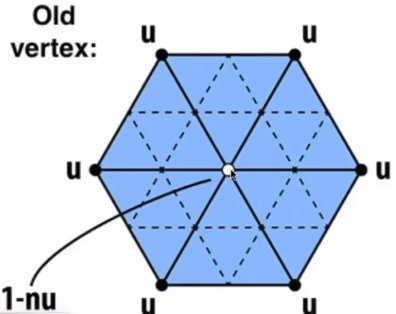
- 对于旧的顶点:假设顶点的度(顶点上边的数量)为
n。每个周围顶点的权重u。最终的计算公式:

# Catmull-Clark Subdivision
# 用于解决多边形下的细分规则。并定义如下几个概念:
- Non-quad face(非四边形面):顾名思义,非四边形。
- Extraordinary vertex(奇异点):度数不为
4的顶点。
对每个非四边形面,得到该面内的「中心点」和各个边的「中点」,然后连接各个「中点」和「中心点」。
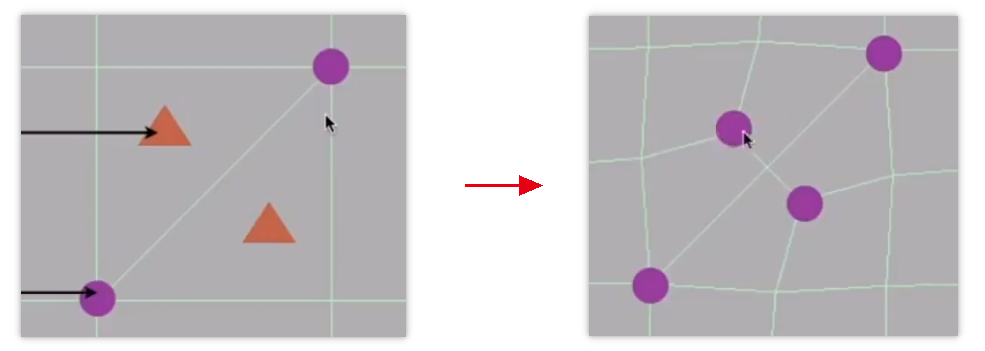
# 最终得到的结果:
- 所有的非四边形面全部消失了。
- 新增奇异点的数量与消失的非四边形面的数量相等。
# 顶点更新规则:
- 在四边形面内的点:
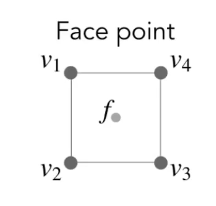
- 在四边形边上的点:

- 四边形各个顶点:
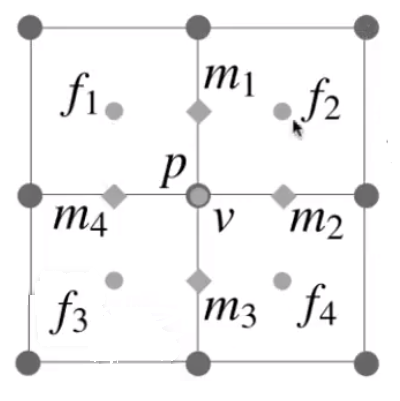
# Catmull-Clark 细分效果:
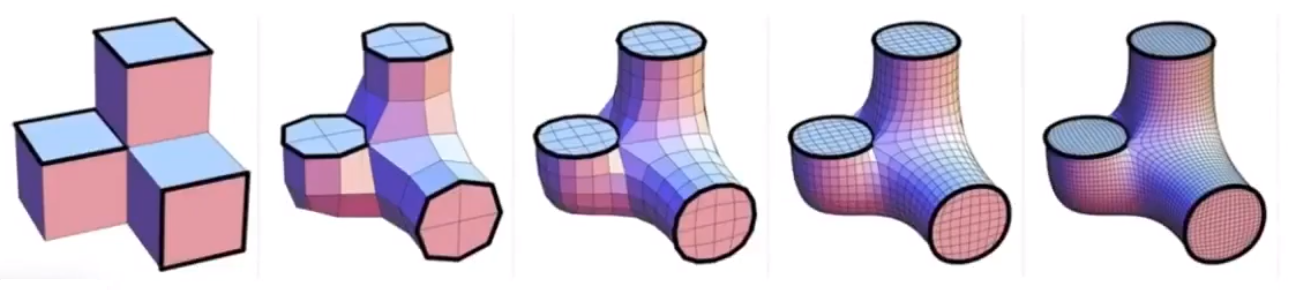
# 网格简化(Mesh simplification)
如何在减小面数的情况下,尽量保持模型的细节。
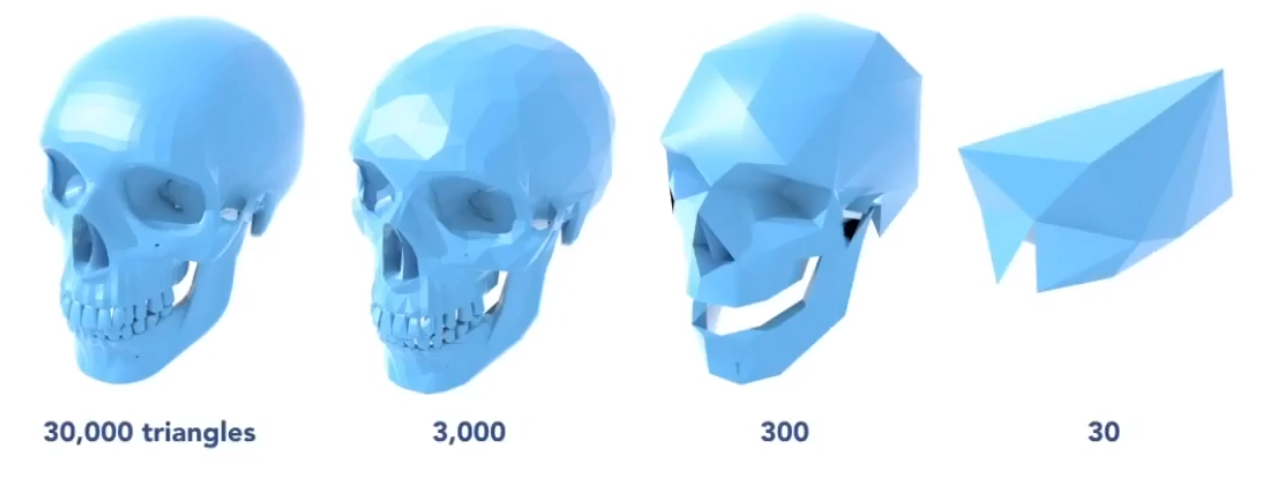
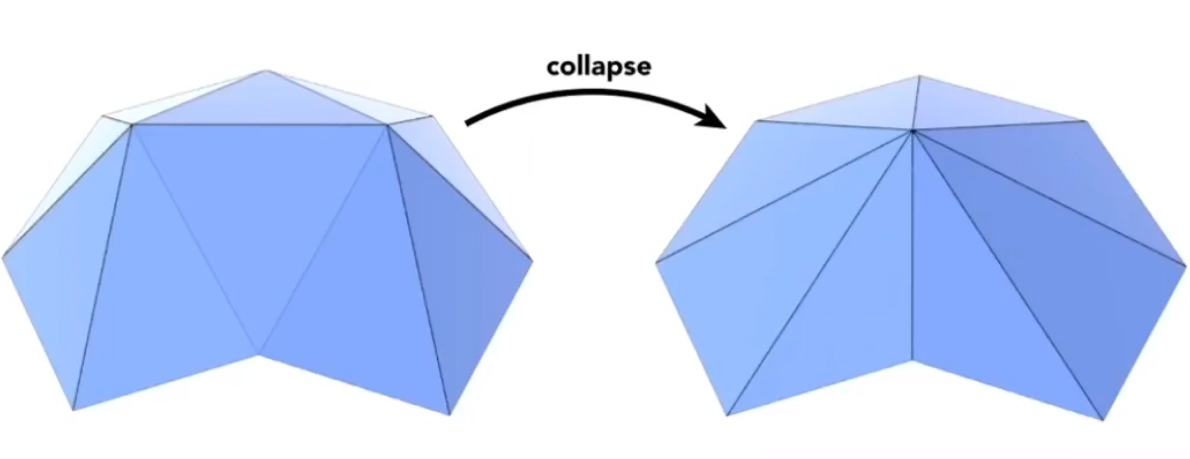
# 边坍缩(Collapsing An Edge)
主要的内容就是合并两个顶点。那么如何决定合并哪些顶点,便成为了问题的关键。
# 二次度量误差(Quadric Error Metrics)
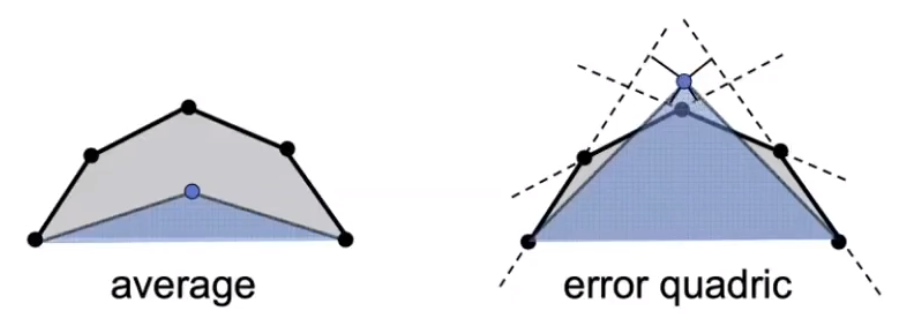
平均法计算最终顶点时,效果往往不够理想,所以引入了一个新的概念 ——「二次度量误差」。
基本理念:计算出一个点,该点到其他点的距离平方和最小。
- 该值便代表了,坍缩这条边的误差值。
- 每次需要坍缩时,就取误差值最小的边进行坍缩。
- 每次坍缩后,其他和这些点关联的边也会发生变化,需要重新计算误差值。
# 二次度量误差的坍缩效果

# 网格正规化(Mesh regularization)
pass