以下为个人学习笔记整理,涉及坐标内容统一用右手坐标系,本节课中所指的「亮度」,均为 Radiance,课程官网。
# 蒙特卡洛路径追踪(Monte Carlo Path Tracing)
# Probabilities
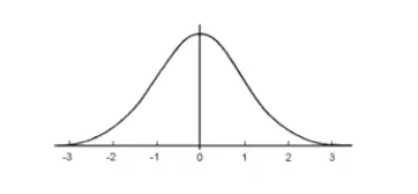
# 概率密度函数(Probability Density Functions)
![image-20210127102344198]()
X∼p(x)
总概率是 1:p(x)≥0&&∫p(x)dx=1
期望:E[X]=∫xp(x)dx
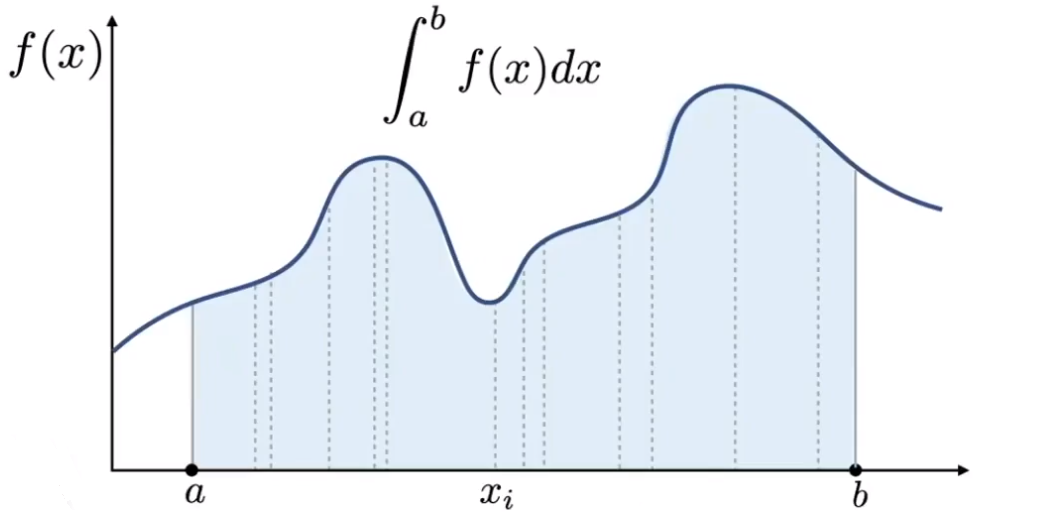
# 蒙特卡洛积分(Monte Carlo Integration)
并不对整个区间求积分,而是在整个区间内做多次均匀的采样。
求得采样的平均值,并把平均值视为区域任何点的 f(x) 值(不规则曲线看成直线)。
![image-20210129173511038]()
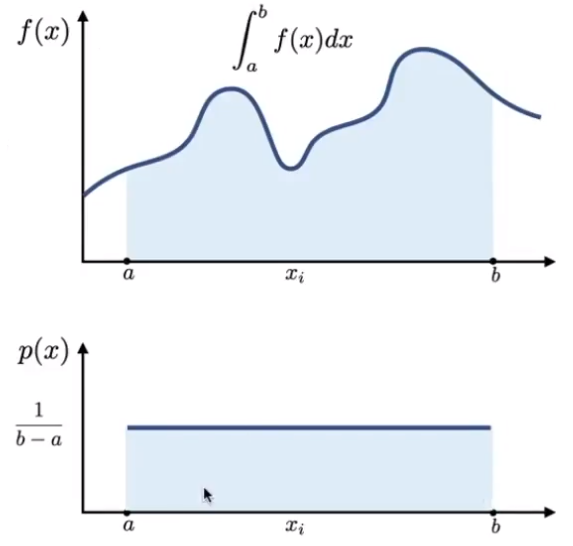
# Definite integral
简单的积分
∫abf(x)dx
把积分曲线视作一个平滑的水平直线
![image-20210130193148210]()
Xi∼p(x)=b−a1
# Basic Monte Carlo estimator
均匀采样 N 个点,再对 N 个点求平均后得到所有点的宽度高度值,乘上 b−a 就能算出积分矩形面积。
FN=Nb−ai=1∑Nf(Xi)
# Monte Carlo Integration
任意采样规则下的蒙特卡洛积分
∫f(x)dx=N1i=1∑Np(Xi)f(Xi)Xi∼p(x)
- 采样点越多,积分越准确。
- 只能在a∼b 的范围内进行采样。
# Path Tracing
# Whitted-Style Ray Tracing
- 始终执行镜面反射和折射。
- 在漫反射物体表面停止反射和折射。
# 遇到的问题
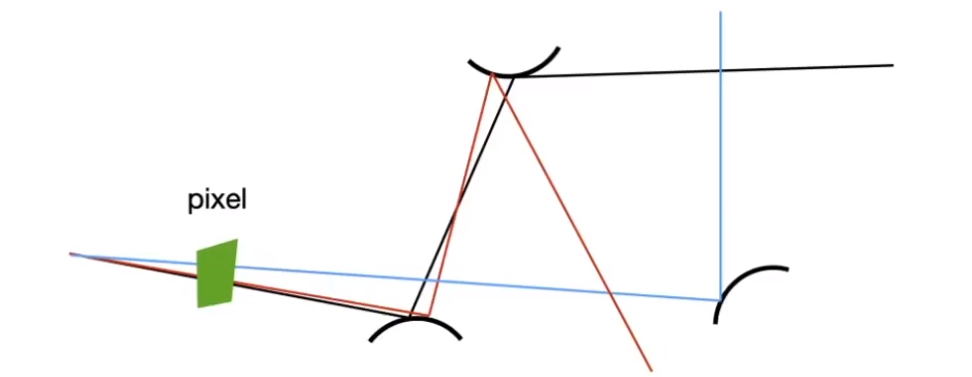
- 对于相对光滑的物体,如何进行光线反射,如何模拟带磨砂的金属。
![image-20210130201422908]()
![image-20210130201922746]()
# Whitted-Style Ray Tracing is Wrong
Whitted-Style 的光线追踪在效果上来说,是不理想的,但是其本身的渲染方程是正确的。
但这个方程的求解本身就比较的困难:
Lo(p,wo)=Le(p,wo)+∫Ω+Li(p,wi)fr(p,wi,wo)(n⋅wi)dwi
# A Simple Monte Carlo Solution
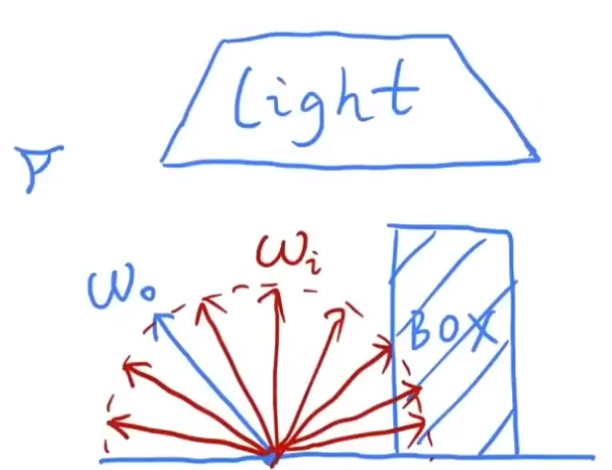
假设只渲染场景中的一个着色点。
![image-20210130202448675]()
假设该点本身是不发光的,所以计算公公式内,不需要计算 Le(p,wo)
![image-20210130202736710]()
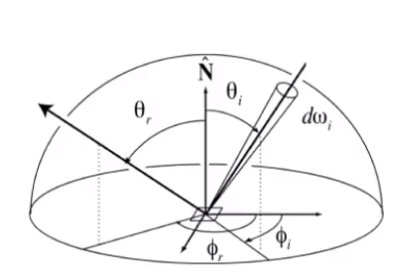
Lo(p,wo)=∫Ω+Li(p,wi)fr(p,wi,wo)(n⋅wi)dwi
所以,计算物体本身在某个方向的光线,需要对物体在整个半球所接受到的光线求积分。
这时候,「蒙特卡洛积分」就闪亮登场了🌟,积分对于整体的计算还是过于耗了,因此进行一个简化:
- 采样某几个点的结果的均值作为最终的积分结果不失为一个不错的选择。
Monte Carlo Intergration:∫abf(x)dx≈N1k=1∑Np(Xk)f(Xk)Xk∼p(x)
其中, f(x) = Li(p,wi)fr(p,wi,wo)(n⋅wi)
PDF:pdf(ωi)=1/2π
因此,对于半球的积分,通过「蒙特卡洛积分」进行多次采样的计算公式可以写成如下形式:
Lo(p,wo)≈N1i=1∑Npdf(wi)Li(p,wi)fr(p,wi,wo)(n⋅wi)
写成代码的形式:
- 从着色点向半球的 N 个方向,射出 N 条光线
- 如果光线最终和点光源有交点,那就计算该光线亮度Lo=Li∗fr∗cosθ/pdf(wi) 。
- 对射出的 N 条光线亮度求平均
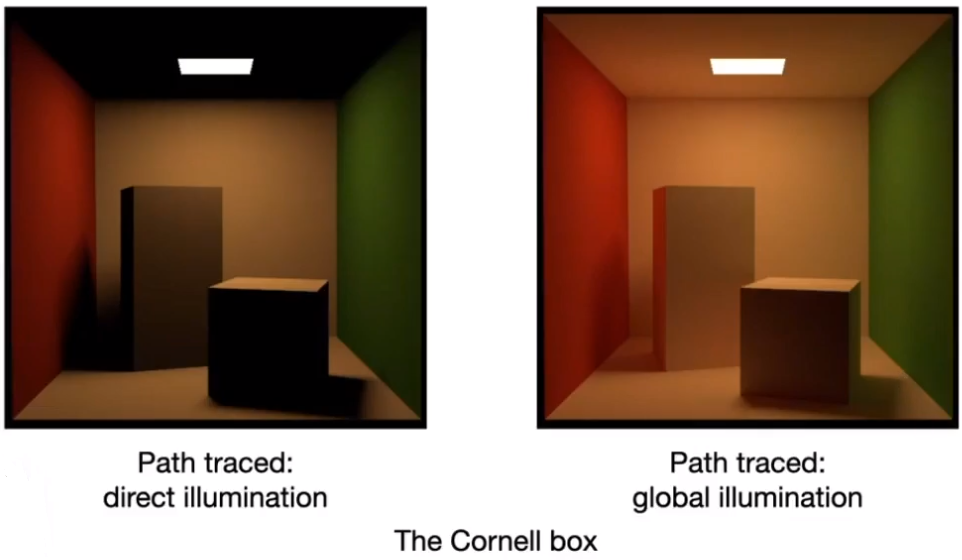
# Inreoducing Global Illumination
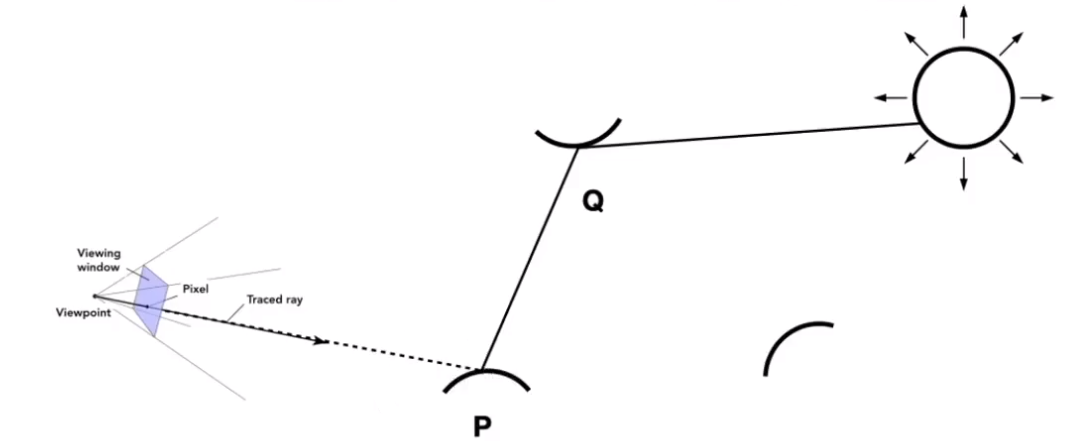
之前叙述的计算蒙特卡洛积分来求着色点问题,没有考虑光线射出后,遇到反射物体的情况。但是在处理全局光照的情况下,这是非常有必要的。
![image-20210130211025384]()
由于物体不仅仅可以接受来自光源的光线,还可以接受来自其他物体反射的光线,因此如果想要得到真实的全局光照,就应该对间接光照进行计算。例如点 Q 提供给点 P 的光照可以简单的视为吧点 Q 作为一个光源,从 P 点对 Q 点进行观察。
写成代码的形式,假设计算该点的着色函数为 shade(p,wo):
- 从着色点向半球的 N 个方向,射出 N 条光线。
- 计算光线和光源交点。
- 如果光线最终和点光源有交点,那就计算该光线亮度 Lo=Li∗fr∗cosθ/pdf(wi) 。
- 如果和反射物体有交点,那就计算反射后的光线亮度 Lo=shade(q,wo)∗fr∗cosθ/pdf(wi) 。
- 对射出的 N 条光线亮度求平均。
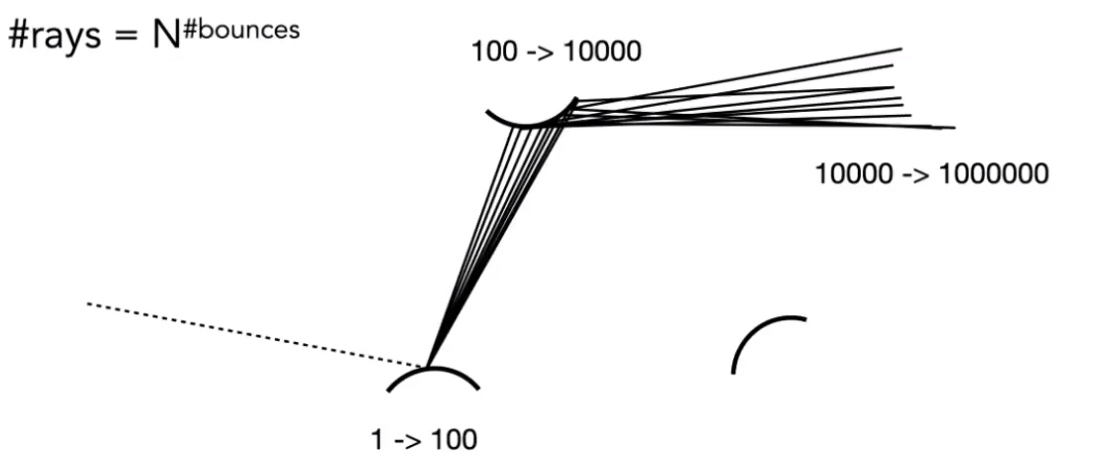
如果递归的计算,当射出的光线数量过多是,计算量级太过庞大。
![image-20210130213323260]()
有没有什么比较好的办法呢?—— 如果只采样 1 条光线。
但是只采样 1 条光线,误差会不会很大呢?因此,为了避免误差产生的噪声,一般会选择多个方向的光线做采样为 1 的「路径追踪」。
当 N 取 1 的情况下,为了降低误差,需要用多个光线穿过着色点进行采样。
- 像素内随机取 N 个点
- 从观察点射出 N 条光线,穿过视点,计算光线追踪。
- 最终把单个像素内的所有点的亮度求平均
![image-20210130213755672]()
# 如果光线一直反射,怎么办
根据之前的计算规则,会计算每次光线反射后的。
但试想一下,如果一条光线一直在进行反射,那么是不是最终就无法计算源像素点的亮度了。
# 解决办法:Russian Roulette(RR)
给追踪一个概率,并非每次光线反射都进行计算。并且,为了避免光线的能量由于概率产生削减,对概率计算进行调整:
E=P∗(Lo/P)+(1−P)∗0=Lo
最终的计算公式 shade(p,wo) :
定义光线发生折射或者反射的概率 P_RR∼[0,1]
- 判断光线是否发生折射或者反射
- 不发生,直接返回 0
- 发生,如果光线击中物体
- 物体如果是光源 Li∗fr∗cosθ/pdf(wi)/P_RR 。
- 物体非光源 shade(q,−wi)∗fr∗cosθ/pdf(wi)/P_RR 。
# 思考
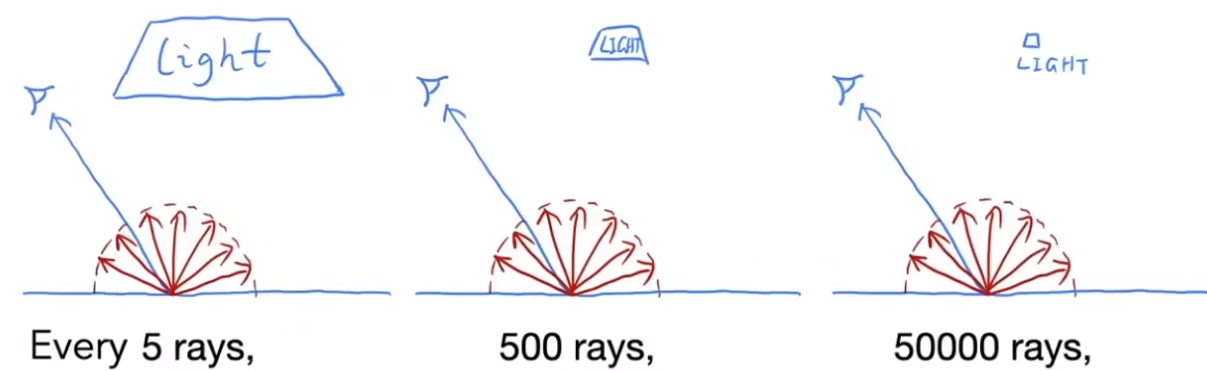
如果光源本身非常非常的小,就算从一个点打出 N 个光线,依然没有一个光线能够和光源有交集,这种情况下的计算将变得非常低效。
![image-20210130220537808]()
# 如何提高效率
为了提高采样效率,可以选择直接在光源上进行采样。
假设光源上是一个二维的平面,面积为 A。那么对 A 区域采样的 PDF 值为 1/A 。
那么在着色点计算半球积分,是否能转化为对光源区域 A 范围内的积分。
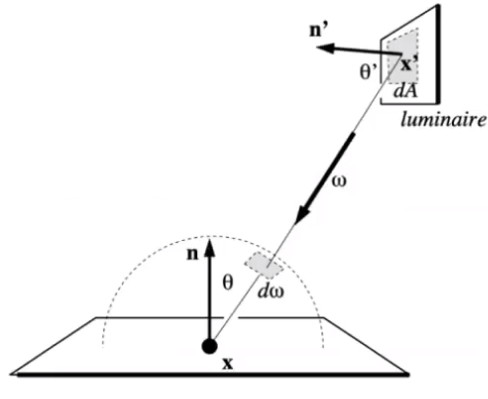
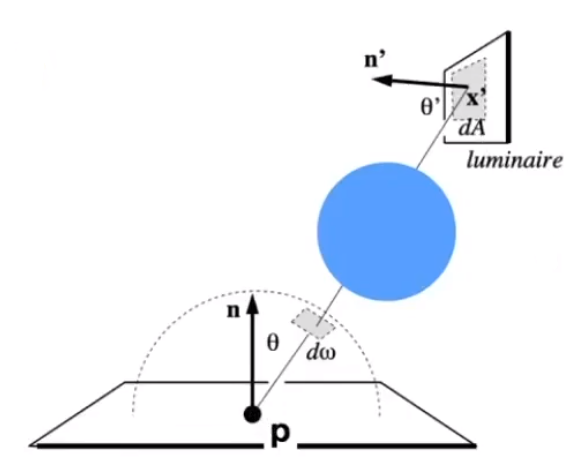
![image-20210130220705421]()
因此需要在 dw 和 dA 之间做个转换。又因为 dw 表示投影到单位圆上的面积,立体角定义,面积 / 距离平方。参考十六课。所以 dA 和 dw 关系如下
dw=∣∣x′−x∣∣2dAcosθ′
重新定义渲染方程,用以光源做积分的形式表示
最终的渲染方程变得异常的简单,只需要对光滑的表面进行积分,再对距离做一定的运算。
Lo(x,wo)=∫Ω+Li(x,wi)fr(x,wi,wo)cosθdwi=∫ALi(x,wi)fr(x,wi,wo)∣∣x′−x∣∣2cosθcosθ′dA
# Sampling the Light
把着色点的光照计算分成两个部分
- 光源对着色点的影响(直接光照,不需要计算 RR 概率)。
- 其他物体反射后对着色点的影响(间接光照,需要计算 RR)。
![image-20210131135024184]()
# 渲染方程
shade(p,wo):
在光源上均匀采样,并计算光线亮度 Llight=Li∗fr∗cosθ∗cosθ′/∣∣x′−p∣∣2/pdf(light) 。
通过 RR 概率,从着色点打出 N 条光线,计算和物体相交的光线亮度并求和。Lother=shade(q,−wi)∗fr∗cosθ/pdf(wi)/P_RR 。
最后对两者求和 Llight+Lother。
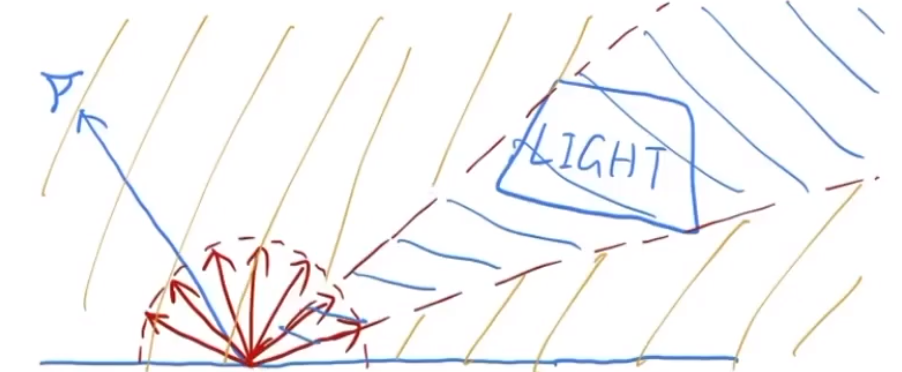
# 思考
如果光源本身被物体遮挡,那么如何计算光源对物体的直接影响呢?
![image-20210131140054630]()
# 最终的渲染方程:
对于被遮挡的光线,直接不计算即可
shade(p,wo):
- 在光源上均匀采样,并求和。
- 如果光线不被遮挡:计算光线亮度 Llight=Li∗fr∗cosθ∗cosθ′/∣∣x′−p∣∣2/pdf(light) 。
- 如果光线被遮挡,直接跳过。
- 从着色点打出 N 条光线,通过 RR 概率,判断发射光线是否需要计算,并求和:
- 需要计算:计算和物体相交的光线的亮度。Lother=shade(q,−wi)∗fr∗cosθ/pdf(wi)/PRR 。
- 不需要计算,直接跳过
- 最后对两者求和 Llight+Lother 。
# 另一个值得思考的问题🤔
如果光源本身是点光源的情况,怎么对光源进行积分,来求直接光照影响呢?
简单的处理办法,可以视作一个较小的面积光源,但并不非最好的解决办法。
# Ray tracing——Previous vs Modern Concepts
# Previous
- Ray tracing == Whitted-style ray tracing
# Modern
- Unidirectional & bidirectional path tracing
- Photon mapping
- Metropolis light transport
- VCM / UPBP
- ...
# 思考🤔
- 如何对半球进行均匀的采样呢?参考资料
- 如果采样不是均匀的,应该怎么处理?(Importance sampling)参考资料
- 如何保证随机数更加的「随机」(low discrepancy sequences)参考资料
- 如果把光源和半球的采样方法相结合,效果会不会更好(multiple imp sampling)
- 为什么把像素上多个点的亮度平均起来,就可以得到像素本身的亮度。需不需要加权?(pixel reconstruction filter)
- 像素的亮度是他的颜色吗?No,需要经过 gamme 矫正(gamma correction,curves,color space)
# 关键字
- Probability Distribution Function(PDF)—— 概率分布函数
- The Cornell Box 传送门