以下为个人学习笔记整理,涉及坐标内容统一用右手坐标系,课程官网。
# 曲线(Curves)
# 贝塞尔曲线(Bezier Curves)
# 德卡斯特利亚算法(Casteljau Algorithm)
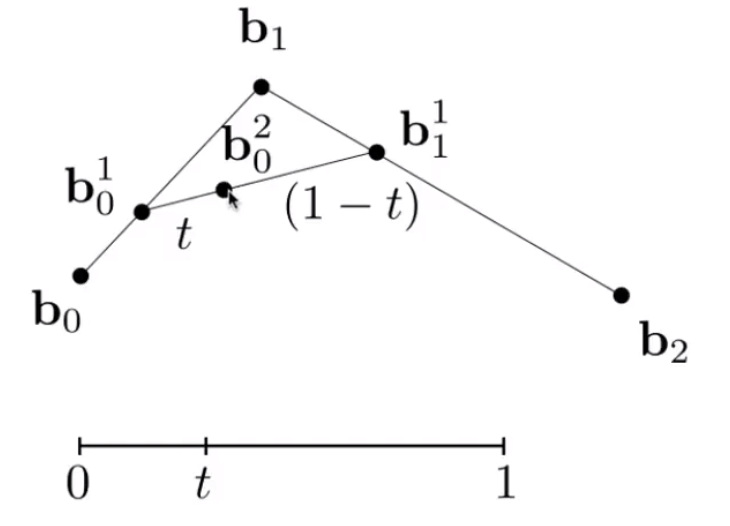
假定绘制一条曲线所需三个点 。曲线的起点为 0 终点 为 1,那么 t 位置处的点如何求得:
- 只需要求 和 的比例 位置的点 。
- 再计算 比例 位置的点 。
- 便是 t 位置处的点。
可以得到 n 个顶点的通用计算公式,该多项式就是 与「伯恩斯坦多项式」的乘积求和。
# 伯恩斯坦多项式(Bernstein Polynomials):
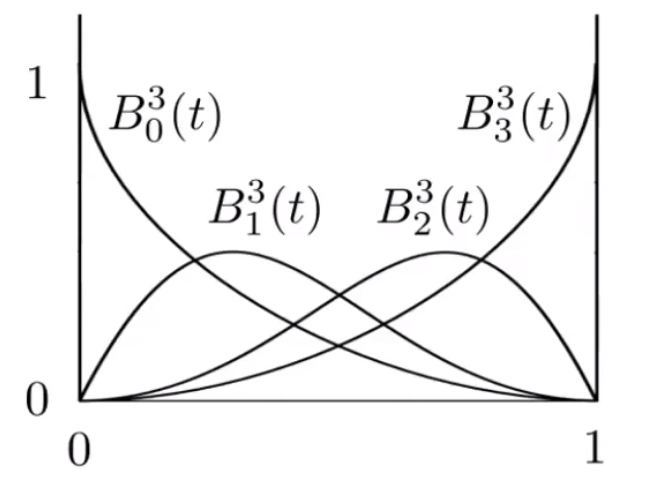
# 贝塞尔曲线的性质
「仿射变换」下,不论是先对顶点进行变换,再绘制曲线;还是先绘制曲线,再进行仿射变换,最终结果一致
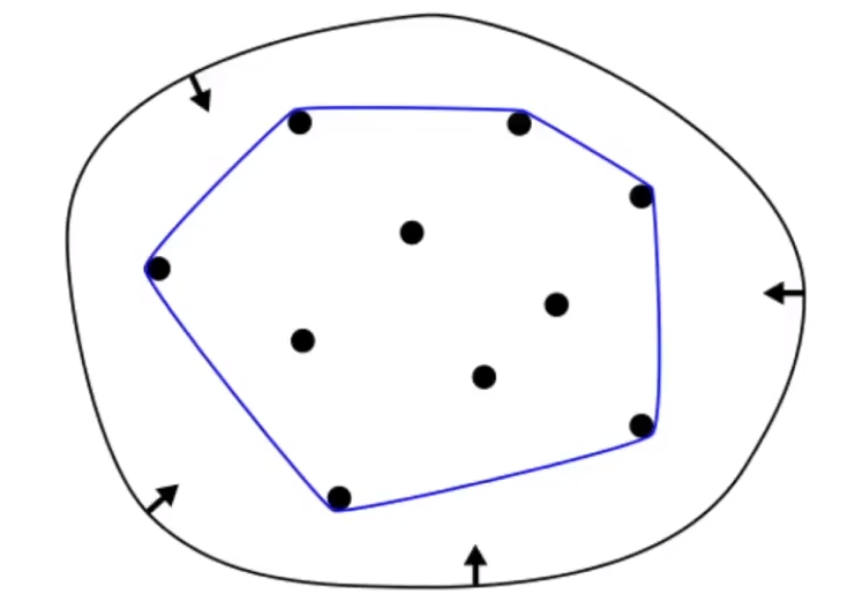
凸包性质:任何贝塞尔曲线内的点,都在形成贝塞尔曲线顶点组成的凸包内。
# 分段贝塞尔曲线(Piecewise Bezier Curves)
由于贝塞尔曲线的每个点,对于整条曲线都会有所影响,想要调整曲线的效果就会变得很麻烦,所以引入了「分段」这个概念。
- 通过多个贝塞尔曲线拼接而成。
- 每个贝塞尔曲线由四个点控制。

# 曲线的连续性
# 连续:两条曲线都过同一个点。
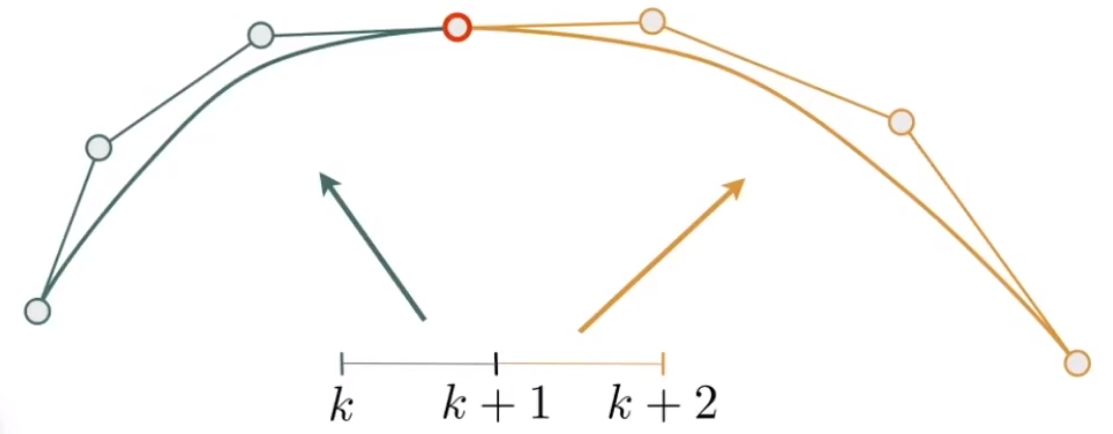
# 连续:两条曲线都过同一个点。且该点左右两边的切线连续(异界导出相同,长度相同)。
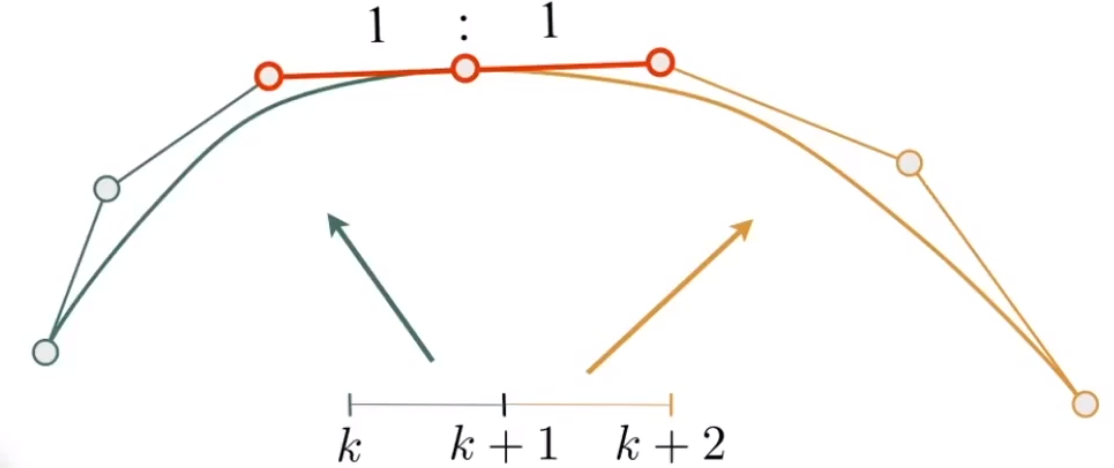
# 连续:pass
扩展视频 —— 如何设计一个逼真的三维模型
# 关键字
- 凸包(Convex):用不严谨的话来讲,给定二维平面上的点集,凸包就是将最外层的点连接起来构成的凸多边形,它能包含点集中所有的点。