# 几何（Geometry）

如何描述不同形状的几何，如何定义光滑的曲面。

# 几何的表示

# 隐式（Implicit）

隐式的表示方法相当于定义了一组规则，即：每个点都可以由函数推导出来。而我们不给出每个点的具体值，只提供推导函数。例如：

• 球体的表示 $x^2 + y^2 + z^2 = 1$
• 通用的定义形式：$f(x,y,z) = 0$

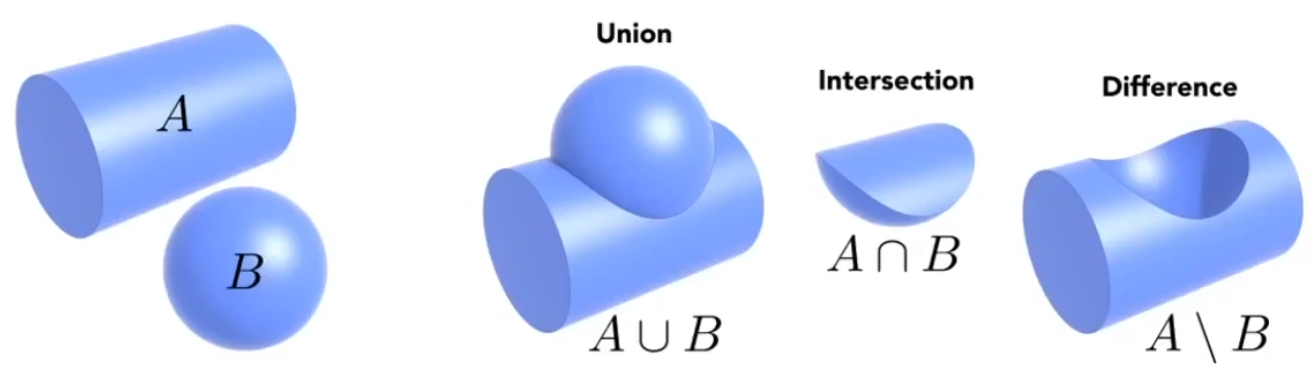
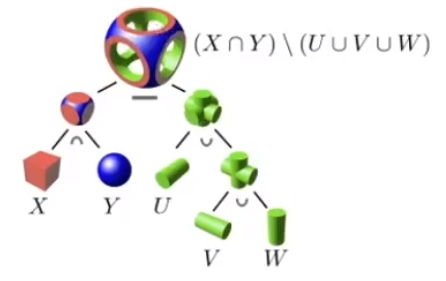
# 构造立体几何（Constructive Solid Geometry）

通过基本几何之间的互相运算，来表示其他的复杂几何。

# 距离函数（Distance Functions）

定义空间中的某个点，几何形体上各个顶点到该点距离，就可以视作一个距离函数。

• 两个几何物体的合并，就可以视为两个几何物体的距离函数的 blending。
• 得到新的距离函数，再恢复成几何物体，就可以得到最终的融合效果。

可以通过 Blend 的方法，得到水滴的融合效果。

# 混合移动边界（Blending a moving Boundary）

通过一个物体两个不同时间的形状，推断出其中间时刻的形状。

例如一个物体在 A 时刻占据了 $1/3$ 的大小，B 时刻占据了 $2/3$ 的大小，那么在 A，B 的中间时刻，按理应该占据 $1/2$ 的大小。

直觉上，以左边界作为原点直接使用 blend 对距离函数进行混合，结果会出现偏差，中间 $1/3$ 的区域会变成半透明状态。

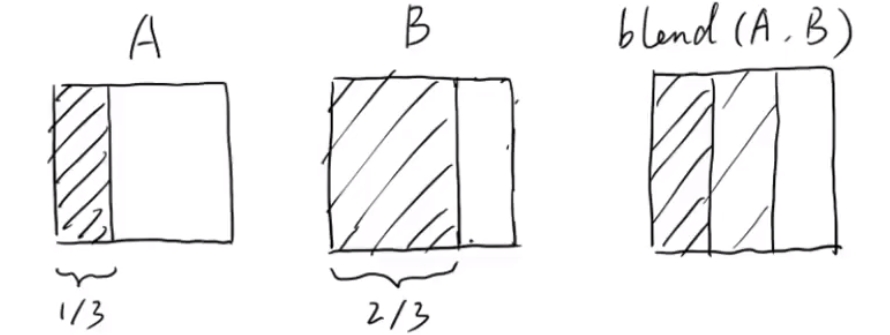
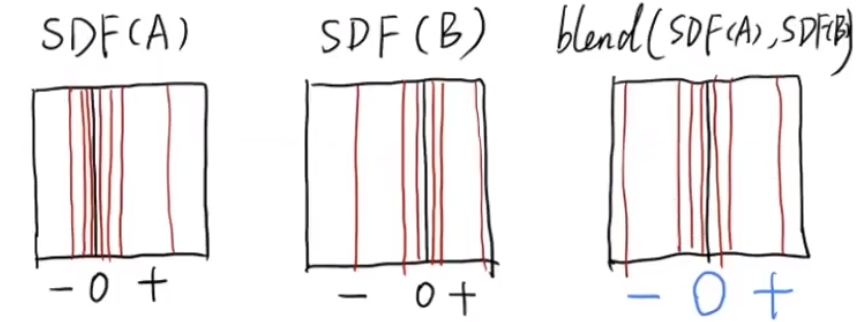
如果把物体的右边界作为原点，使用 blend 对距离函数进行混合，才能得到正确的混合效果。

# 距离函数到几何物体

最直观的办法就是求得距离函数上所有距离为 0 的位置给求出来，就可以形成几何物体的表面。

$$f(x) = 0$$

# 水平集方法（Level Set Methods）

当某些情况下，距离函数不太好写成解析形式（求 $f(x) = 0$ 比较困难）的时候，就可以通过「水平集方法」来粗略的得到边界。

通过求得每个格子的距离值，来大致的估算最终为 0 的边界。

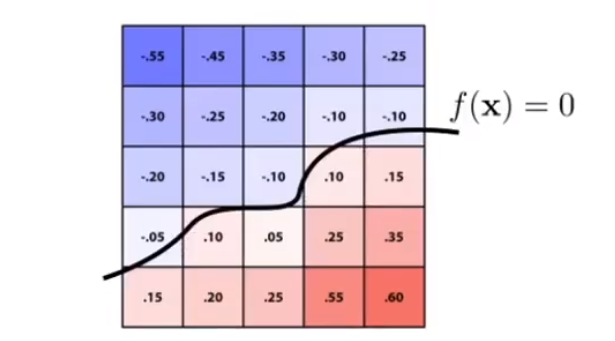
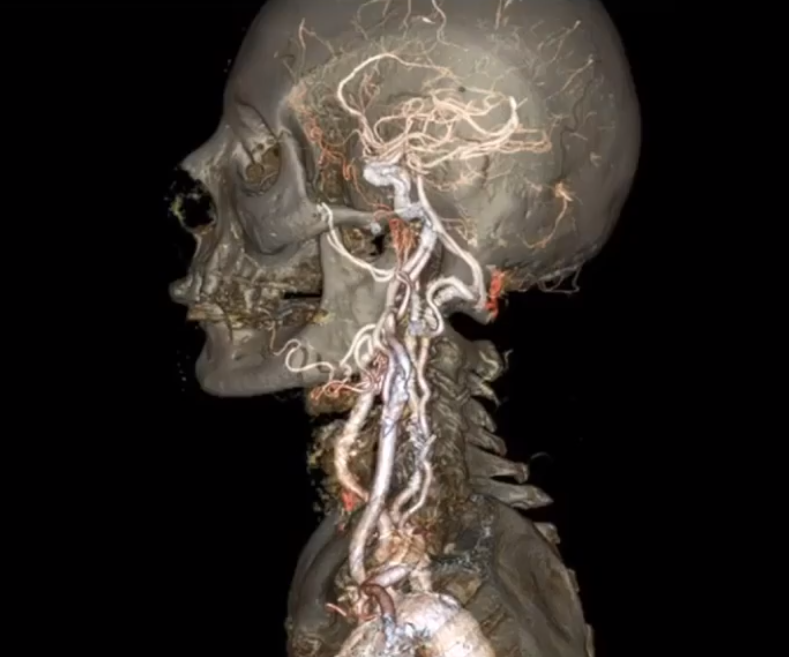
通过定义一个水平级（恒定组织密度），来得到某一类物体的表面轮廓（组织器官的轮廓）

# 分形（Fractals）

类似递归的概念。

# 优缺点

• 优点：
  • 表示简单，占用空间小。
  • 判断判断空间中的一个点是否在该物品表面（内 or 外）非常的简单。
  • 对于光线求交的计算比较方便。
  • 描述简单集合更加的严谨和精确。
  • 易于处理拓扑变化。
• 缺点：
  • 很难给复杂的几何建立隐式的表示。

# 显示（Explicit）

要么直接给出三维空间中的坐标，要么通过定义一个 $(u,v)$ 到 $(x,y,z)$ 的映射的函数。

$$f:R^2 \to R^3; (u,v) \to (x,y,z)$$

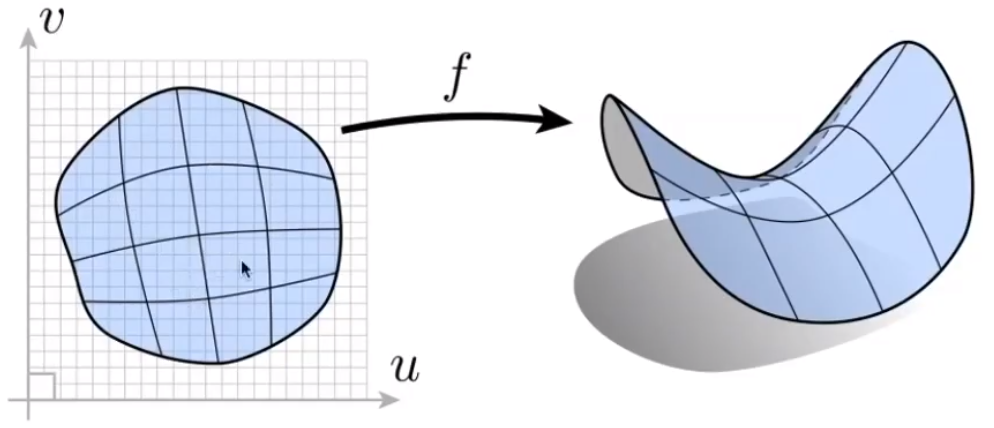
# example

$$f(u,v) = ((2 + \cos u) \cos v, (2 + \cos u) \sin v, \sin u)$$

# 点云（Point Cloud）

用一个个的点，来绘制想要的图形。

# 多边形网格（Polygon Mesh）

通过顶点和多边形组成图形。

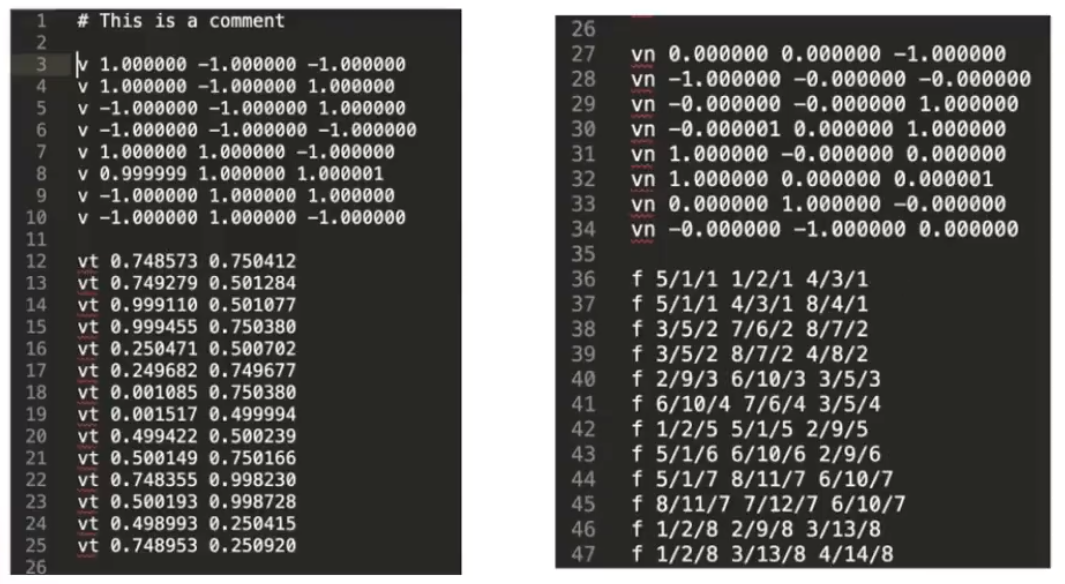
# 常见的多边形网格表示（.obj file）

下图表示的是一个空间中的立方体。

• v x y z ： v 表示是顶点， x y z 表示立方体的每个顶点的坐标。
• vn x y z ： vn 表示各个面的法线， x y z 表示各个面的法线方向。
• vt x y ： vt 表示纹理坐标， x y 表示顶点的纹理坐标值 u v 。
• f v_number\vt_number\vn_number ： f 表示构成面的顶点， v_number 表示顶点编号， vt_number 表示纹理坐标编号， vn_number 表示法线编号。

# 优缺点

• 优点：
  • 表示复杂的图形比较简单
• 缺点
  • 但要判断一个点是否在几何图形上（内 or 外）比较困难
  • 占用空间较大