以下为个人学习笔记整理,涉及坐标内容统一用右手坐标系,课程官网。
# Antialiasing
# 瑕疵(Artifacts)
通过采样得到的图像往往会有些许瑕疵🏸
- 锯齿(Jaggies)

- 摩尔纹(Moire)

- 视觉错觉(Wagon wheel illusion)

# WHY?
信息的变化速度超过了采样的速度。且信息变化的越快,往往「瑕疵」越明显。
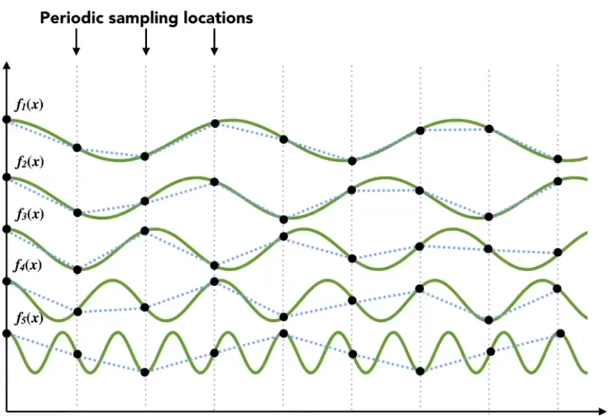
# 走样
相同的采样频率下,对下图的两种波形,没办法很好的区分开。这样的结果被称之为走样。
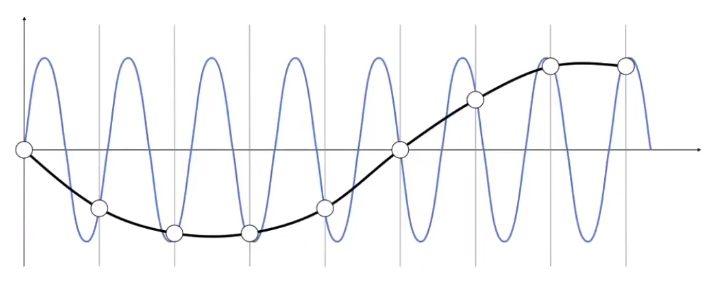
# 傅里叶变换(Fourier Transform)
任何一个函数都可以通过一系列变化,得到另一个函数。
# 傅里叶级数(Fourier series)
任何函数都可以通过多个 和 函数加上一个常数来表示。
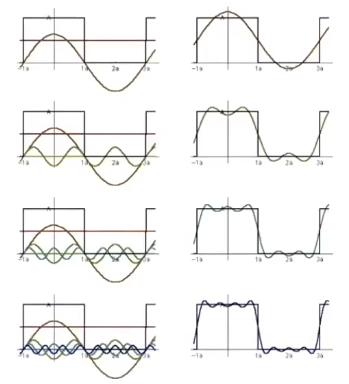
# 可视化图像频率内容
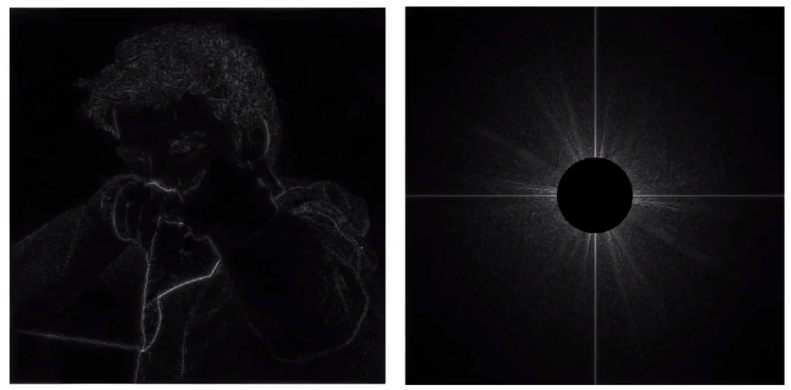
把图片(左边)的信息转换为表示高、低频率的图像(右边)。
- 右图中,中心区域的频率最低,往四周逐渐增大。
- 右图中,亮和暗表示图片在高低频率上的分布情况,中心越亮表示图片大部分内容都集中在低频段。
- 右图中的两长线,表示图片的边界。由于分析信号的过程中,会把信号视作一个周期变化的,而图片信号实际上就是将多个相同的图片进行平铺得到的,所以边界处的差异会比较大,频率会相应的更高。

# 高通滤波(Hight-pass filter)
通过把图片信号转为频率图片,再把其中的低频内容过滤,之后反推回之前的图像,就能得到图像内的高频内容(图像的轮廓)。
# 低通滤波(Low-pass filter)
过滤掉了高频率内容,只留下低频内容。最终的图片变得模糊(失去了明显的边界)

# 如果过滤掉高、低频,结果如何呢❔

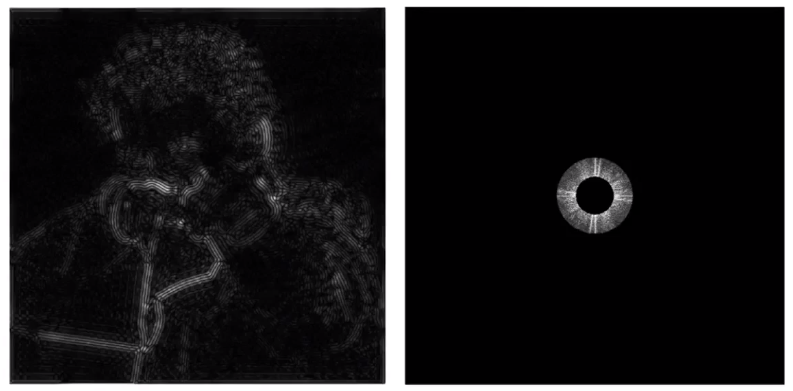
# 过滤、平均、卷积(Filtering、 Averaging、Convolution)
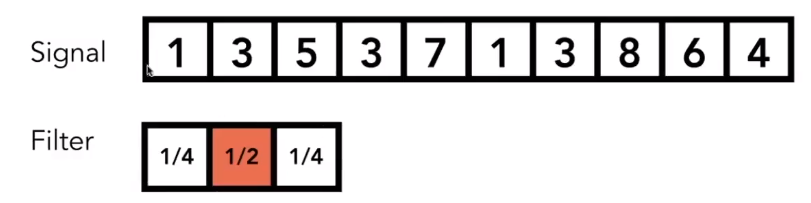
# 卷积
滤波器和信号相同位置进行点乘再相加,得到的结果放回滤波器中心所在的位置。看起来就像是对某片区域的数进行一个加权平均操作。

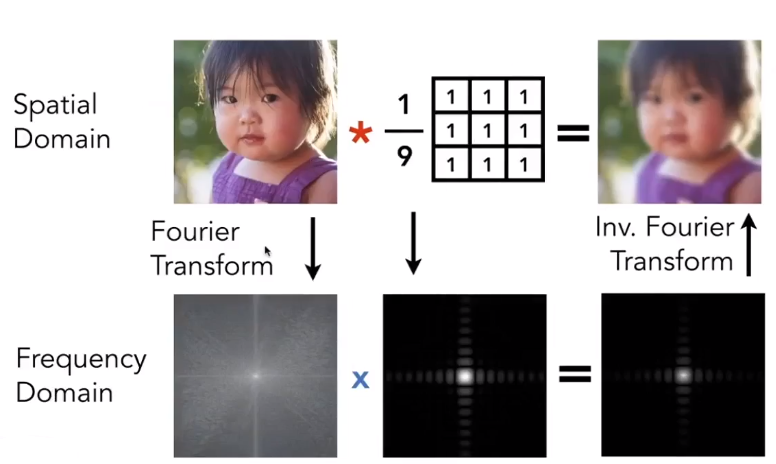
# 卷积定理
时域的乘积等于频域的卷积
图像矩阵点乘卷积核得到的结果,等同于把图像和卷积核通过傅里叶变换,再相乘得到的结果,在进行「逆傅里叶变换」还原到的图像。
# 抽样 = 重复(Sampling = Repeating)
图左是一个时域上的函数,假设右图是该函数在频域上的分布
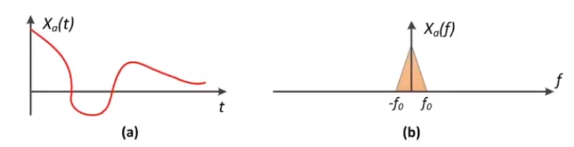
通过冲击函数对其进行采样,(时域的乘积等于频域的卷积)
- 冲击函数:只在某个 t 值上,有对应的 P 值。
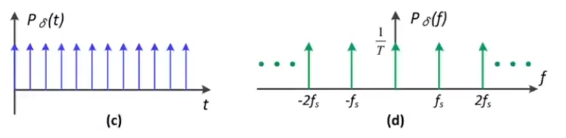
最终得到的采样结果:频域上的卷积,就像是对频域上的内容进行平铺。

# 走样的根源
采样间隔越小,频域之间的步长就越大,反之则反之。
如果采样的间隔过大,则会导致频域之间出现叠加,导致走样。
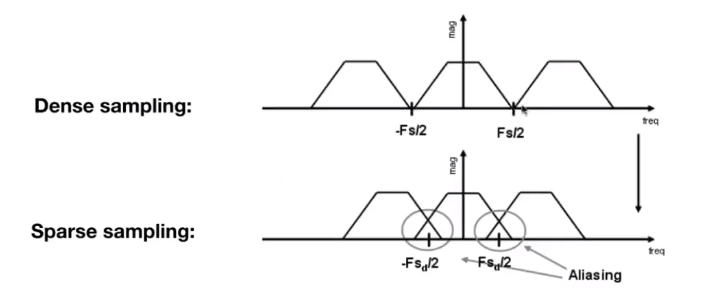
# 反走样
# 先砍掉高频信号(模糊操作,去边界),再进行采样。
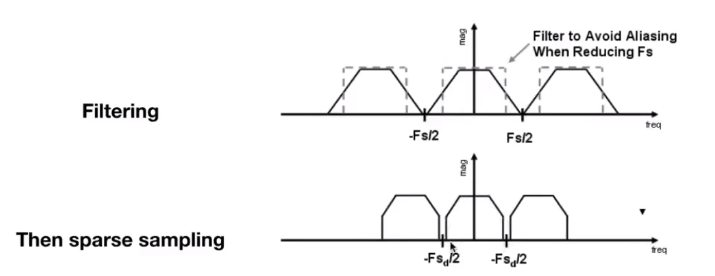
# 为什么不能先采样,再去高频?
如果先采样,再把高频部分重叠给去掉。
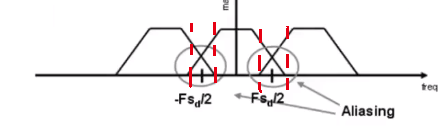
如果只截取高频那么还是会有混叠
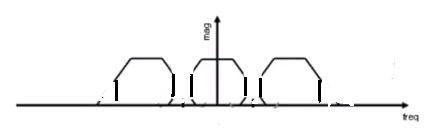
如果把混叠全部截断对比于先模糊再采样,两个频域之间的间隔就变大了。
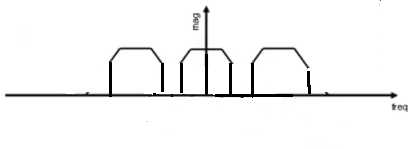
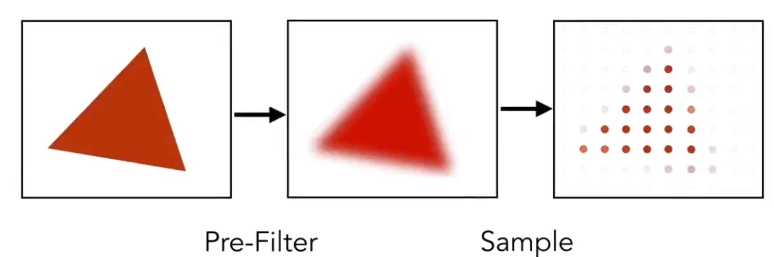
# 如何进行低频滤波(Pre-Filter)
对一个像素点内部求平均,但是由于计算量较大所以没有这么做。
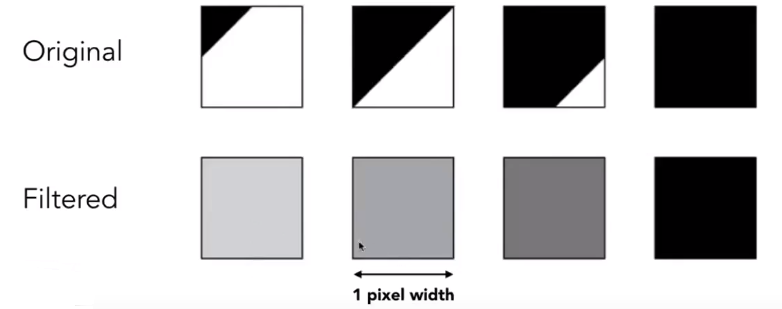
# 多采样抗锯齿 (Multisample Anti-aliasing)
MSAA 实际上不能完全解决锯齿。仅仅是对像素值做了一个平均。
对于任意的一张图像:
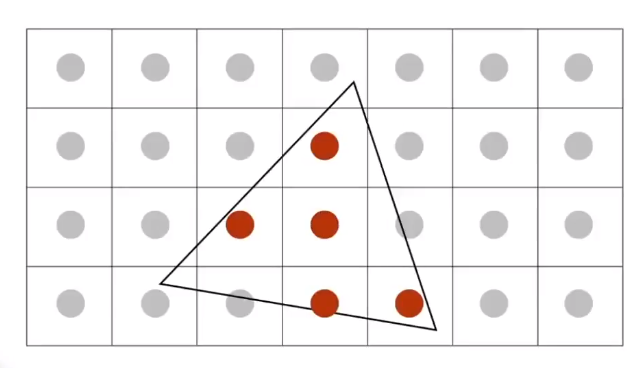
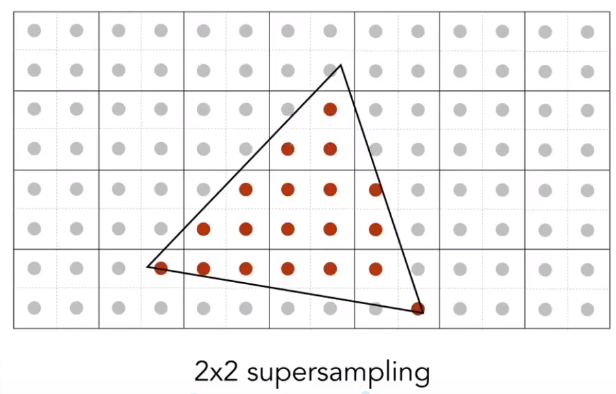
把每个像素拆分成 nxn 的子像素
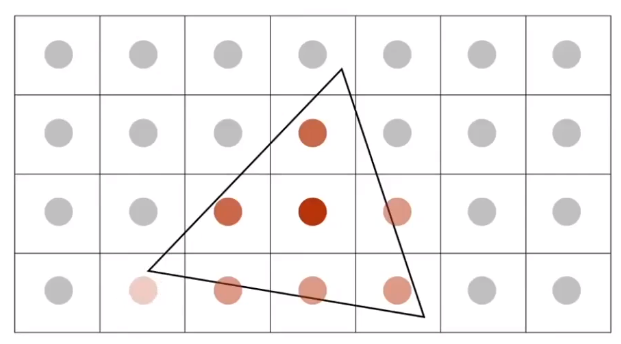
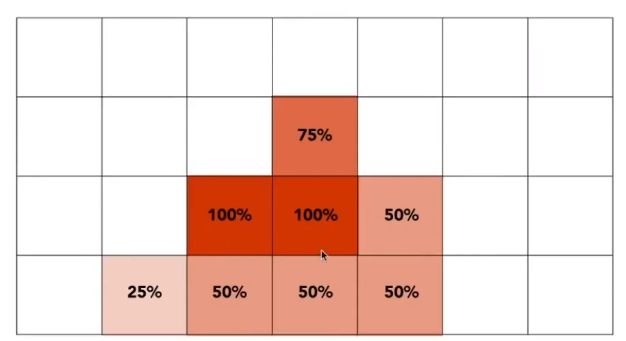
通过计算子像素的「覆盖率」,对像素颜色进行深浅的插值。
最终的效果就像是做了一个模糊操作。
# MSAA 相关优化:
- 边缘 MSAA
# Fast Approximate AA(FXAA)
图像的处理,替换边界。
# Temporal AA(TAA)
提取上一帧的结果,不对本帧的像素做拆分。而是把相同帧的不同时间段的像素值做 MSAA
# 超分辨率
扩大图像的分辨率,但保持图像的清晰
- Deep Learning Super Sampling(DLSS)
# 关键字
- 多采样抗锯齿 (Multisample Anti-aliasing):简称 MSAA
- 傅里叶变换(Fourier Transform)
- 卷积(Convolution)