以下为个人学习笔记整理,涉及坐标内容统一用右手坐标系,课程官网。
# Animation
# Single Particle Simulation
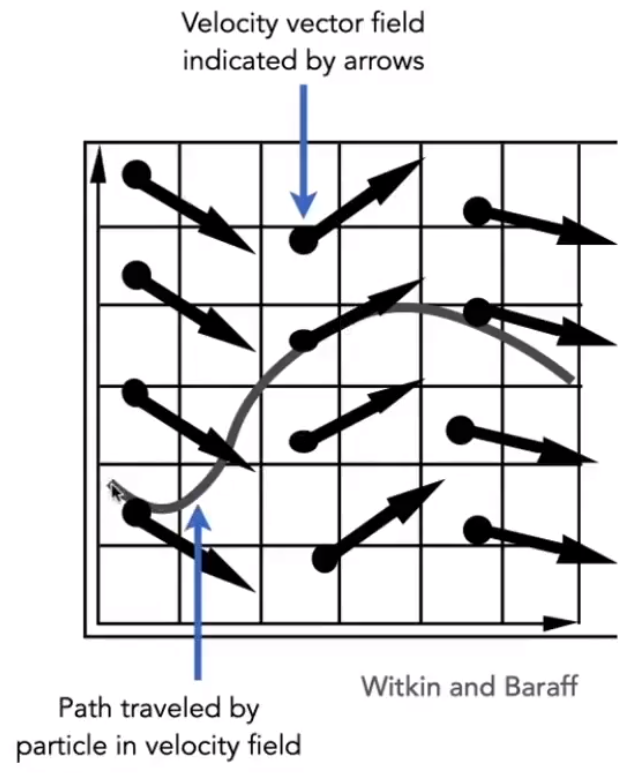
先从单个的粒子开始,假设物体的运动由一个速度矢量场决定,不同位置不同时间粒子会获得不同方向不同大小的速度 v(x,t) 。
![image-20210207164348850]()
# Ordinary Differential Equation(ODE)
定义一个一阶的常微分方程(ODE),用于计算物体的速度 v 。
dtdx=x˙=v(x,t)
![image-20210207164643815]()
# Solving for Particle Position
通过常微分方程(ODE),在已知位置 x0 的情况下,求解 x˙ 。
# Euler Method
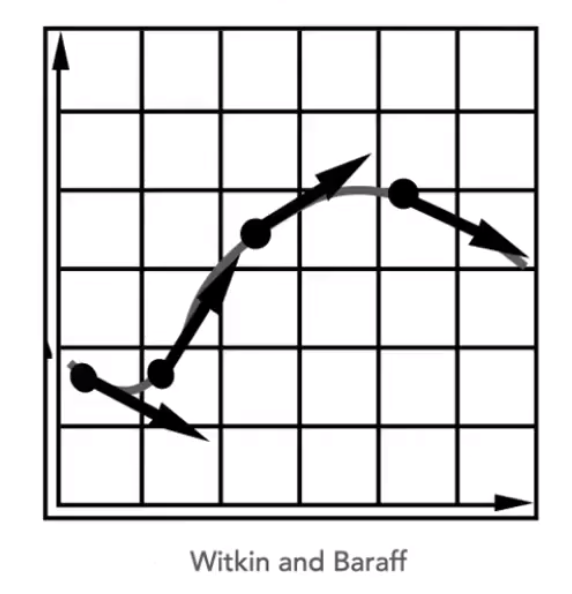
通过当前状态推断下一个阶段的状态。
xt+Δt=xt+Δtx˙t
x˙t+Δt=x˙t+Δtx¨t
# Euler Method Errors
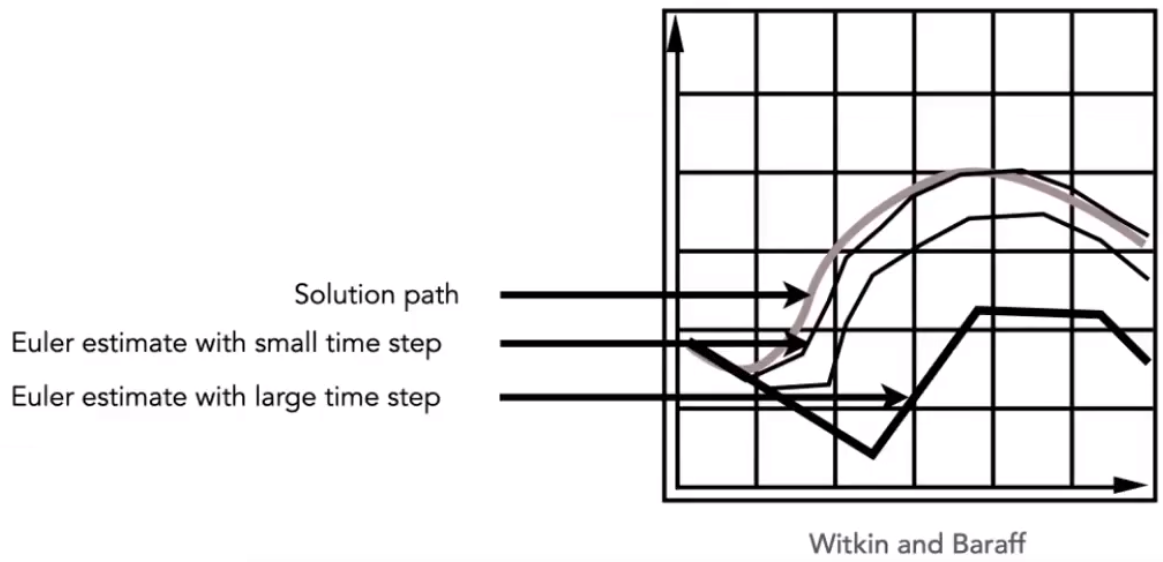
![image-20210207165735695]()
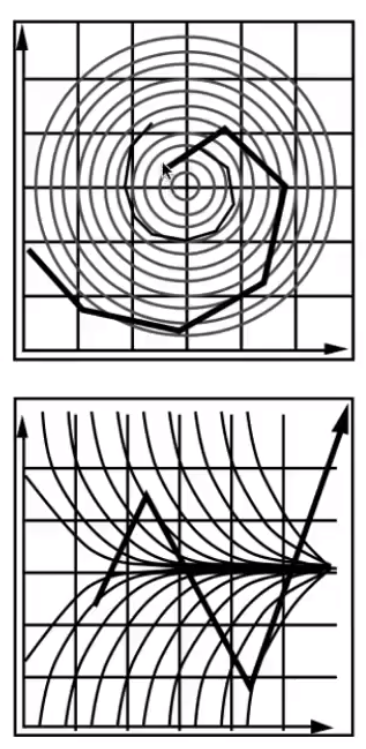
- 欧拉方法的不稳定性(Instability):由于每个位置的方向都不一致,导致不论步长取多大,都会出现一定的偏差。
![image-20210207165826660]()
- 误差可以通过减小步长来弥补,但是不稳定性却无法解决。
# Combating Instability
- Midpoint method / Modified Euler
- Adaptive step size
- Implicit Euler method
- Position-based / Verlet integration
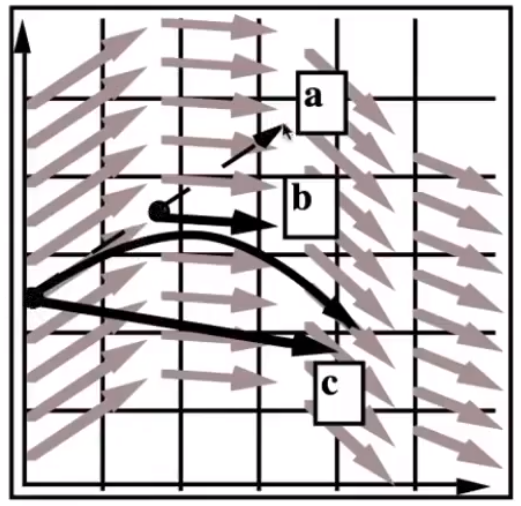
# Midpoint method
- 通过起始位置和方向,计算下一个目标点 a 。
- 计算起点和目标点 a 的中点 b 的速度。
- 把 b 点的速度应用在起点,得到下一个目标点 c 。
![image-20210207170921947]()
xmid=x(t)+Δ/2⋅va(x(t),t)=xb
x(t+Δt)=x(t)+Δt⋅vb(xmid,t)=xc
Modified Euler:
假设起点为xo:xct+Δt=xot+2Δt(x˙ot+x˙at+Δt)
xat+Δt=x˙ot+Δtx¨ot
xct+Δt=xot+Δtx˙ot+2(Δt)2x¨ot
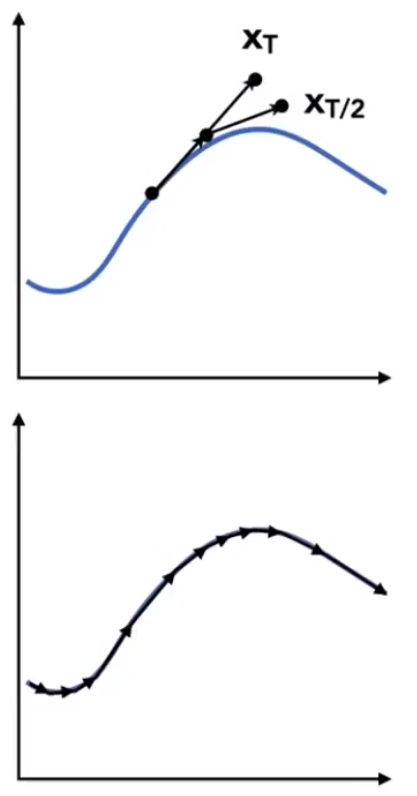
# Adaptive Step Size
- 计算一个步长后的结果 xT 。
- 对计算结果减半后再中点处,在计算一次半个步长,得到另一个点 xT/2 。
- 比较两个点之间的误差是否在可接受范围。
- 大于预期误差,继续细分。
- 小于预期误差,应用 xT/2 。
- 最终就可以得到一个动态变化步长的细分曲线。
![image-20210207173559994]()
# Implicit Euler Method
相比于常规的 「Euler Method」,「Implicit Euler Method」的区别在于,使用的是下一个 Δt 下的速度、位置、加速度来更新上一个 Δt 。
xt+Δt=xt+Δtx˙t+Δt
x˙t+Δt=x˙t+Δtx¨t+Δt
# 如何定义「Instability」❓
局部误差 (local truncation)「every step」/ 总误差(total accumulated)「overall」 的比值的阶和 Δt 的关系。
- Implicit Euler
- Local truncation:O(h2) 。
- Global truncation:O(h) 。
O(h) 表示,h 如果减小到一半,全局误差也减小到一半。O(h2) 表示如果 h 减小到一半,局部误差减小到 41 。
# Runge-Kutta Families
一系列用于求解「ODE」的方法。
- 对于非线性的情况效果较好。
- 其中一个四阶方法 ——RK4,被广泛运用。
初始条件:dtdx=f(x,t),x(t0)=x0
R4方程:tn+1=tn+Δtxn+1=xn+61Δt(k1+2k2+2k3+k4)
其中:k1,k2,k3,k4→k1=f(tn,xn),k2=f(tn+2Δt,xn+k12Δt),k3=f(tn+2Δt,xn+k22Δt),k4=f(tn+Δt,xn+Δtk3)
# Position-Based / Verlet Integration
基于非物理的一些规则定义物体的位置使得物体看上去符合现实中的某些规律。
- 效率高且计算简单。
- 非物理导致可能出现能量不守恒等其他问题。
# Rigid Body Simulation
刚体的模拟,可以当作一个粒子去看待。
dtd⎝⎜⎜⎜⎛XθX˙ω⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛X˙ωF/MΓ/I⎠⎟⎟⎟⎞⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡X: 位置θ: 旋转角度X˙: 速度ω: 角速度F: 力M: 质量Γ: 力矩I: 转动惯量⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
# Fluid Simulation
# A Simple Position-Based Method
基于位置的方法,把流体视作一个个的粒子,并计算每个粒子的位置信息,就能模拟出流体的运动。
- 假设水在任何地方都不可压缩 —— 粒子是刚体。
- 且在任何时刻,水的密度都需要趋近于平稳状态下的密度,通过「纠正」每个粒子的位置信息。
- 需要计算每个粒子所在位置的梯度密度,这样如果某个位置的粒子运动将会影响附近的粒子跟着运动。
![image-20210208102743045]()
# Eulerian vs Lagrangian
# 质点法(Lagrangian Approach)
观察的基本单位是一个个的点,考虑任意时间点上,每个点的位置变化。
![image-20210208110629997]()
# 网格法(Eulerian Approach)
观察的基本单位是一个个的网格,考虑单位时间内,每个网格的状态变化。
![image-20210208110638096]()
# Material Point Method(MPM)
混合型方法,考虑「Lagrangian」和「Eulerian」。
- 遵从粒子的特性来考虑物体的材质属性。
- 物体的变化通过网格的形式来计算。
- 计算得到的网格数据应用到格子内的每个粒子上。
![image-20210208111601277]()
# oceans of stars