以下为个人学习笔记整理,涉及坐标内容统一用右手坐标系,课程官网。
# Physical Basis of Color
# The Visible Spectrum of Light
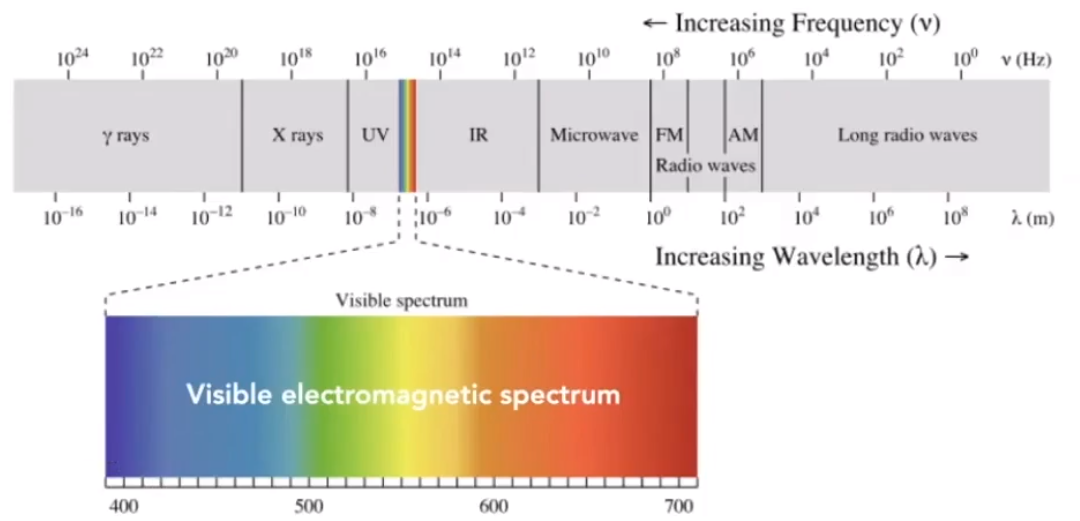
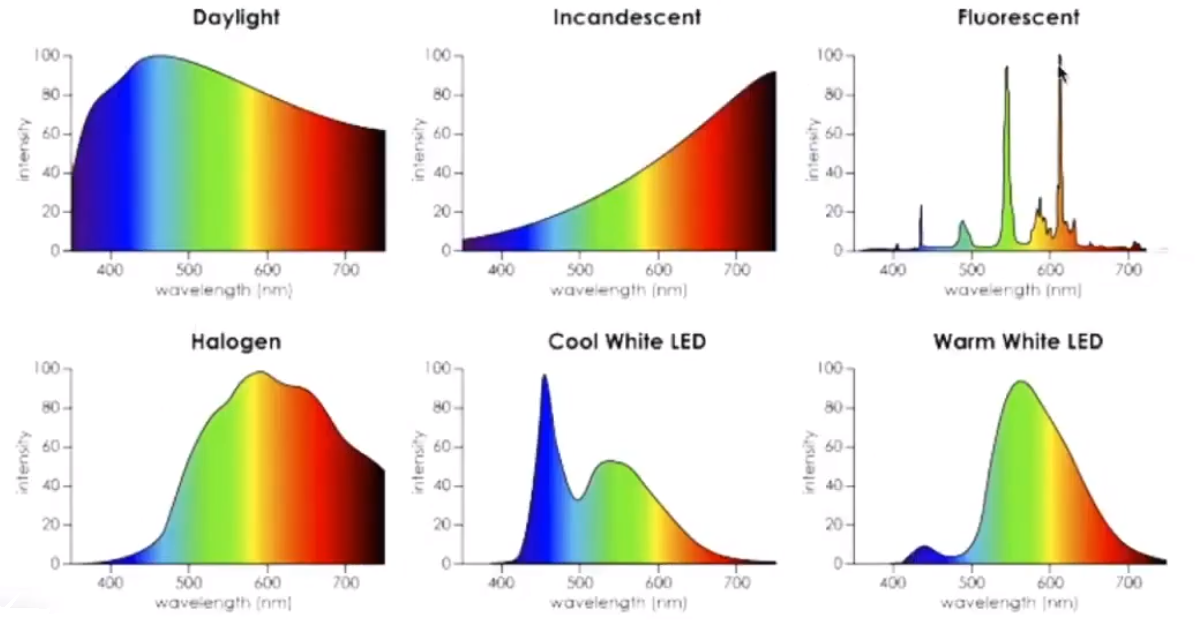
# Spectral Power Distribution(SPD)
光谱率密度(SPD)表示:在某个波长下的光线功率。
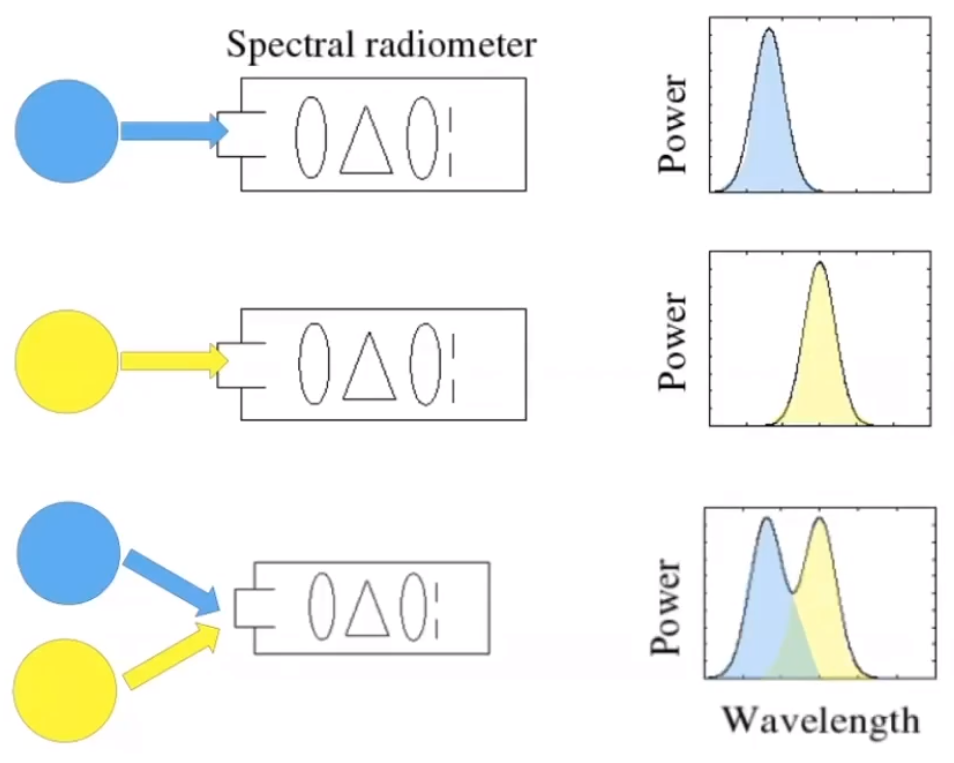
# Linearity of Spectral Power Distributions
光谱率密度满足线性的特性。两种相关同时照射一个物体,两个光线的「谱光率密度」会叠加。
# What is Color
颜色只是人对于不同波长的光线的一种感知。
# Biological Basis of Color
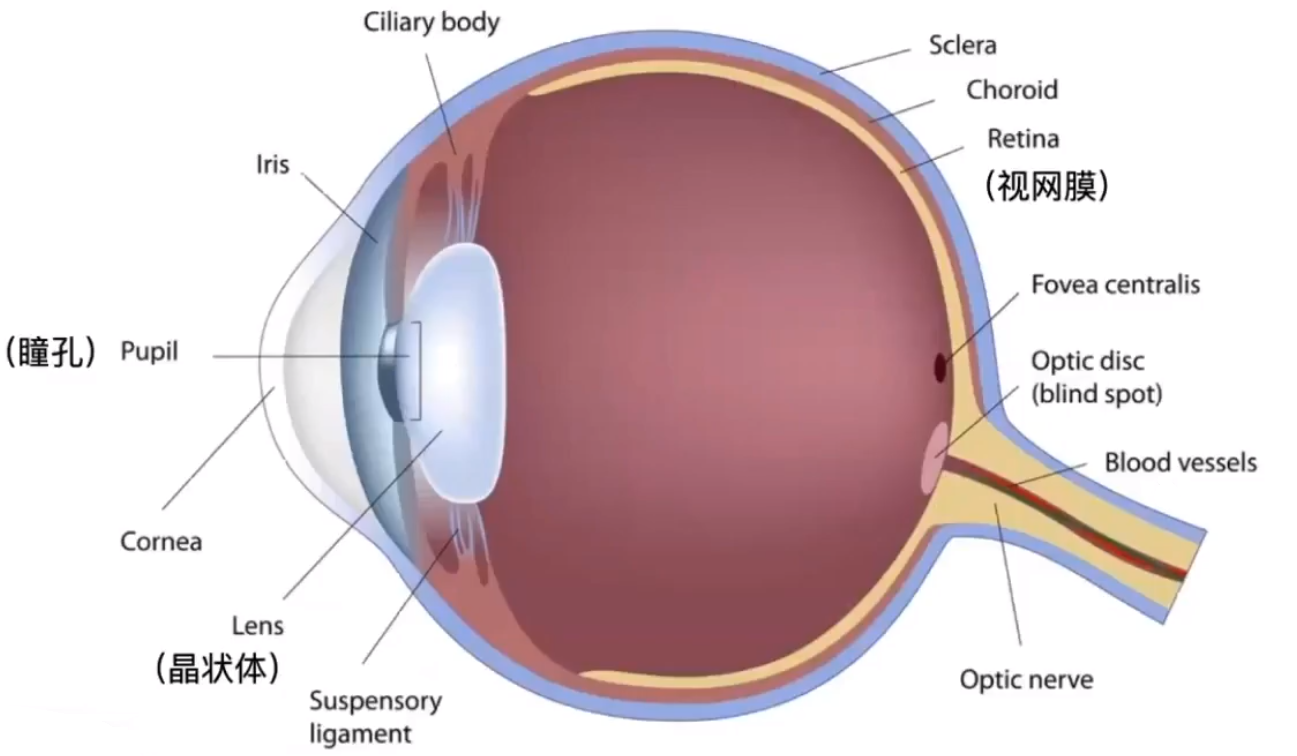
# Retinal Photoreceptor Cells:Rods and Cones
- Rods Cells:感知光线强度的细胞。
- Cones Cells:感知光线的波长(颜色)。
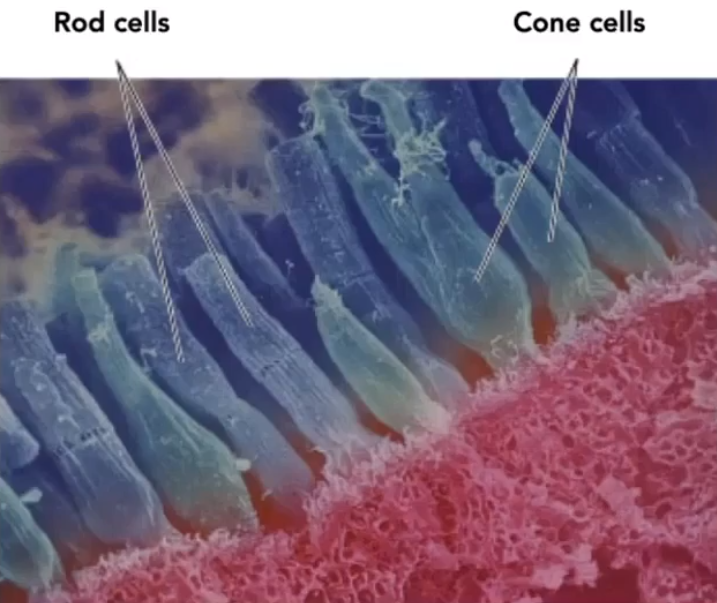
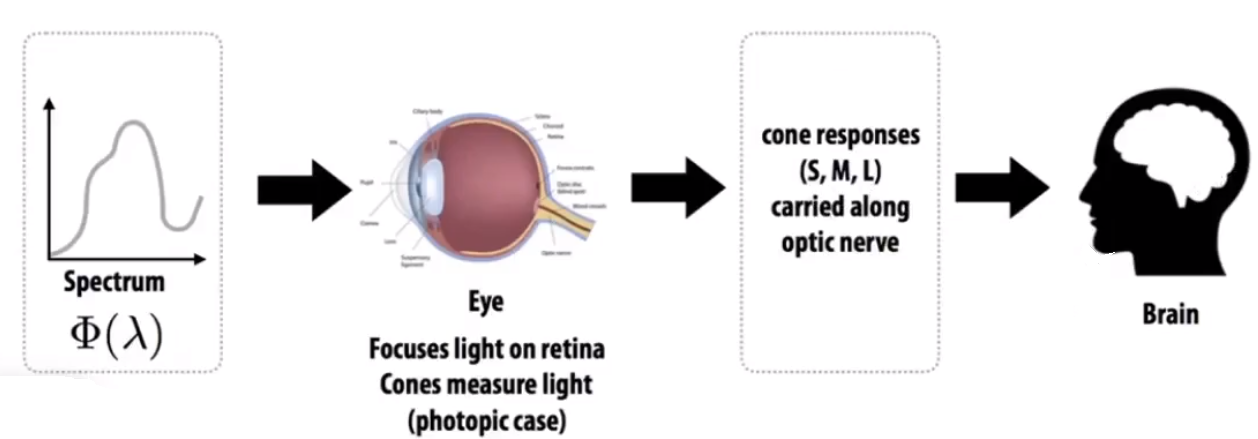
# Spectral Response of Human Cone Cells
「Cones Cells」细胞又可以分成三类(S、M、L):三种细胞对于不同波长的光线感知程度也不一样。
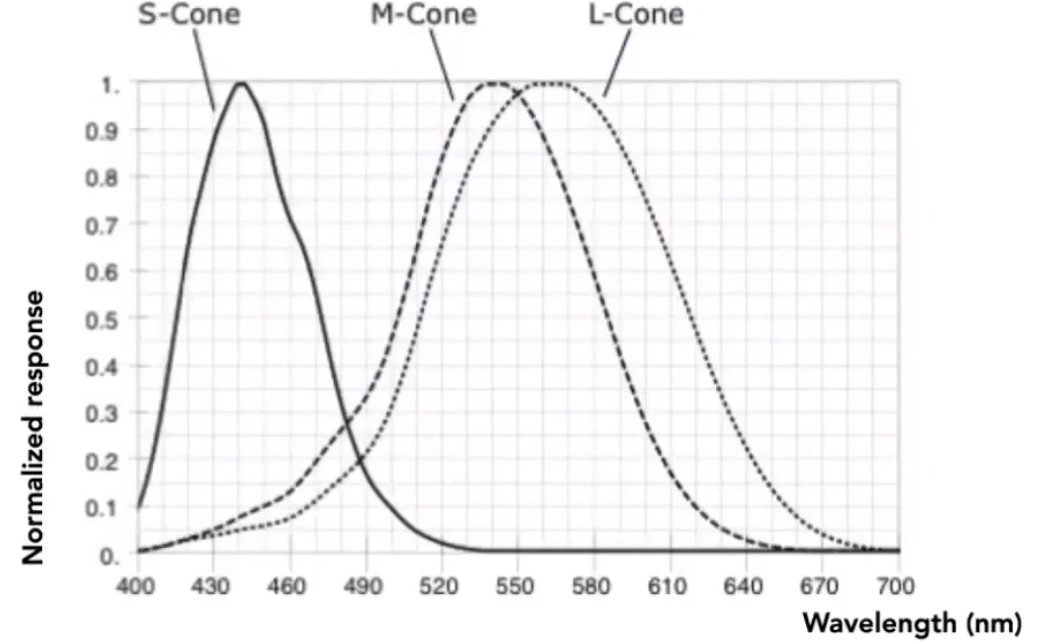
已知一个光谱的情况下,用光谱上各个波长的光线强度和感知强度求积分,就可以得到三个值(S、M、L)。通过不同的 S、M、L 值,就可以表示一个光谱。
这样就可以通过 S、M、L 来表示我们所看到的颜色。
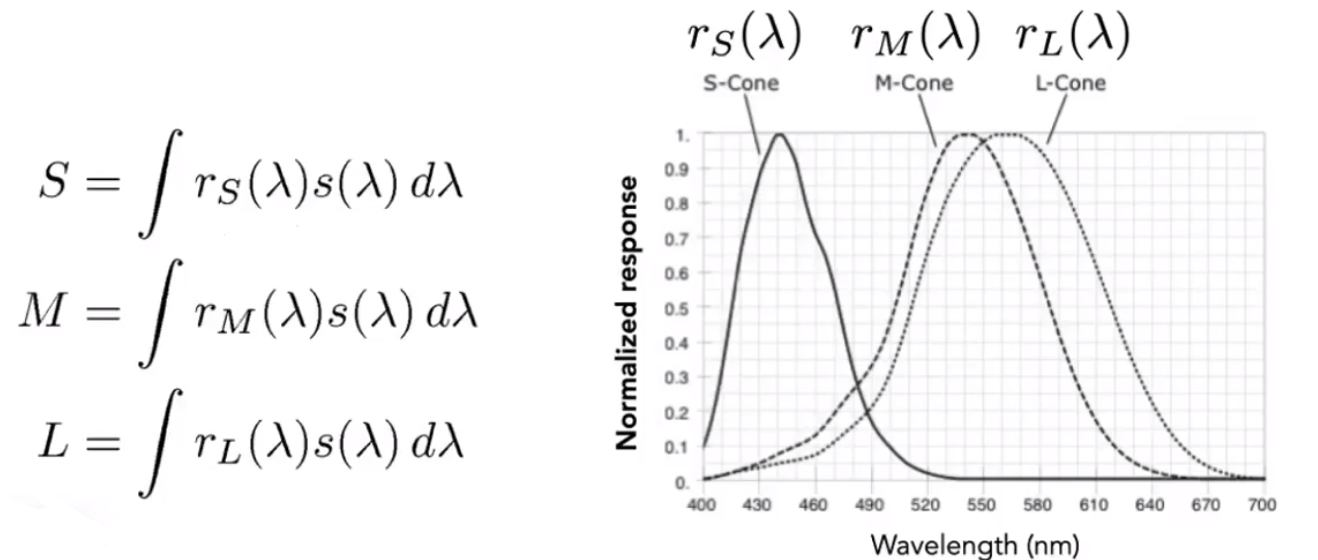
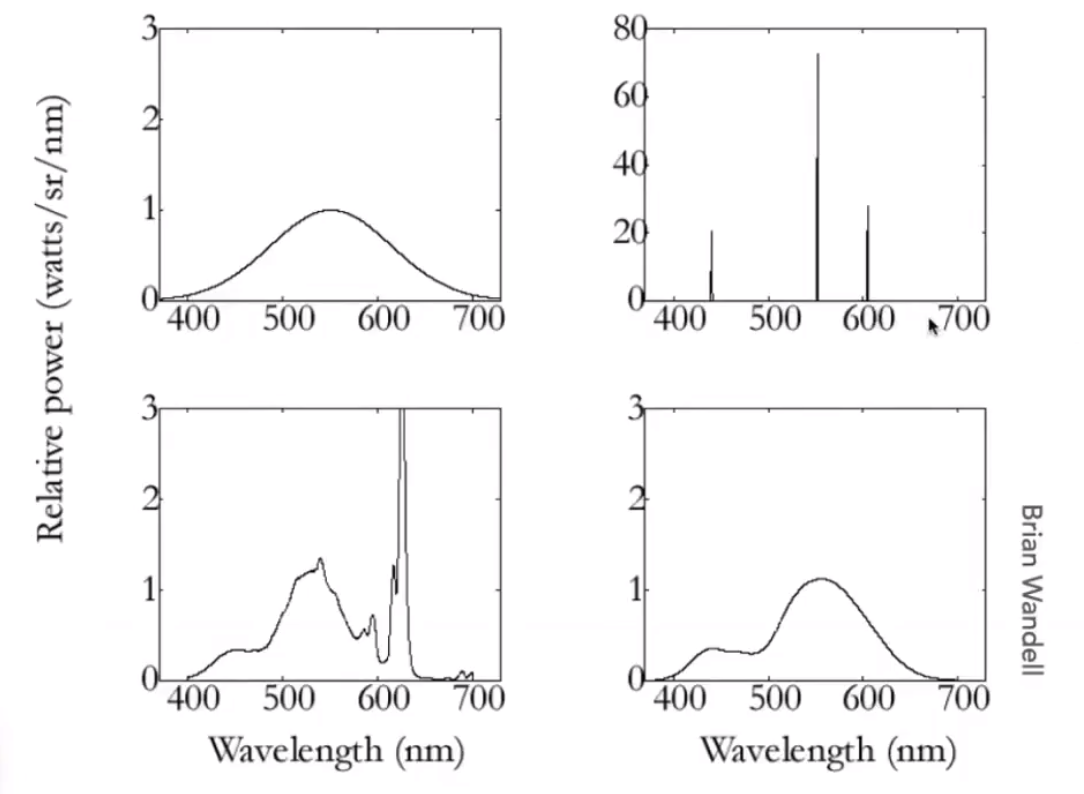
# Metamerism
有没有可能出现相同的 S、M、L 但是光谱却是不同的呢。—— 答案是可能。
左边和右边的光谱,最终的 S、M、L 值相同。
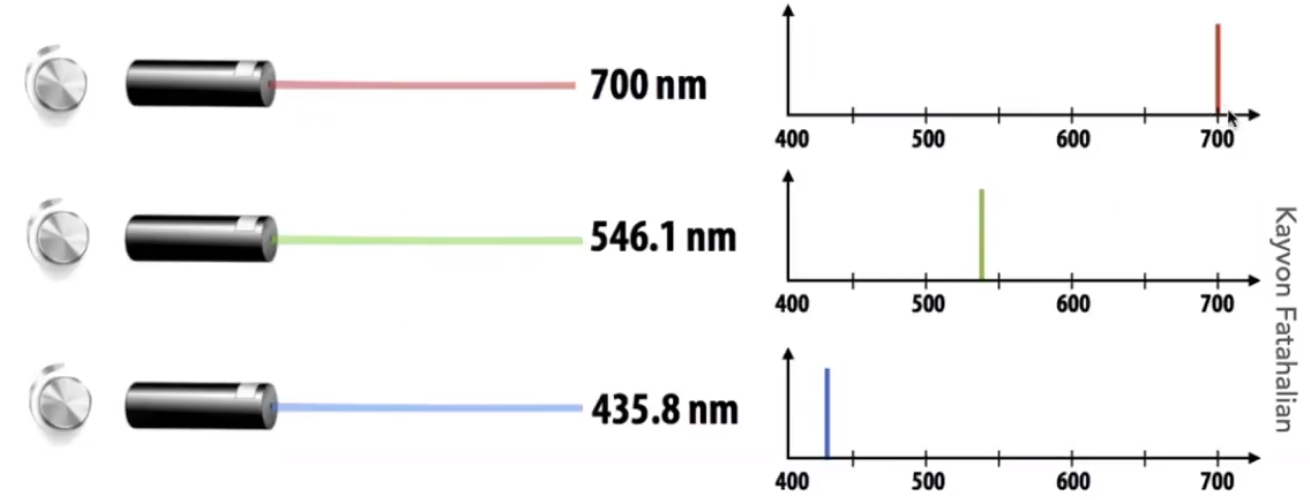
# CIE RGB Color Matching
为了能够得到任意颜色的光线,可以先假定三种颜色的光线,并通过一定强度的混合,从而获得新的颜色的光线。
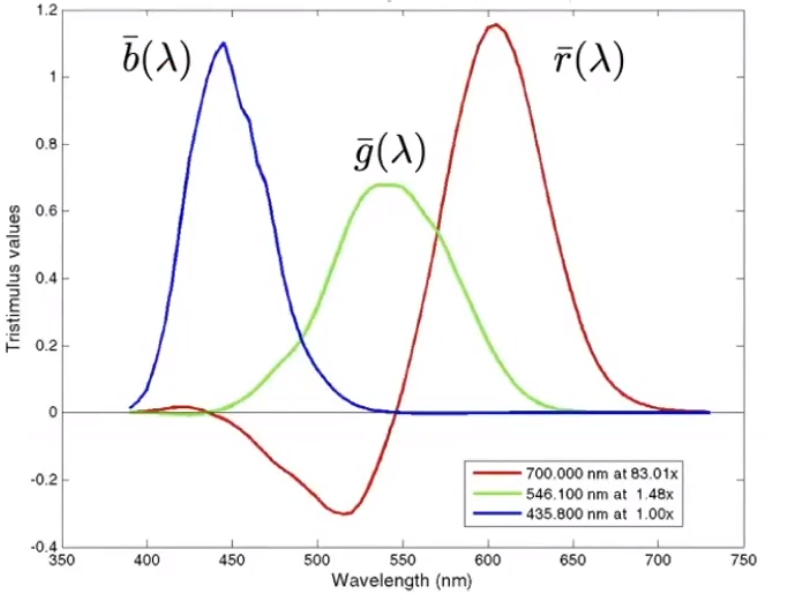
# CIE RGB Color Matching Function
由此,如果我需要得到特定波长的光。就可以用一定系数的 rgb 三种颜色的光效表示。
# Color Reproduction with Matching Function
因此,如果需要模拟一个完整的光谱。对匹配函数进行积分,并把任意波长位置的光线用 RGB 三种光线系数代替。
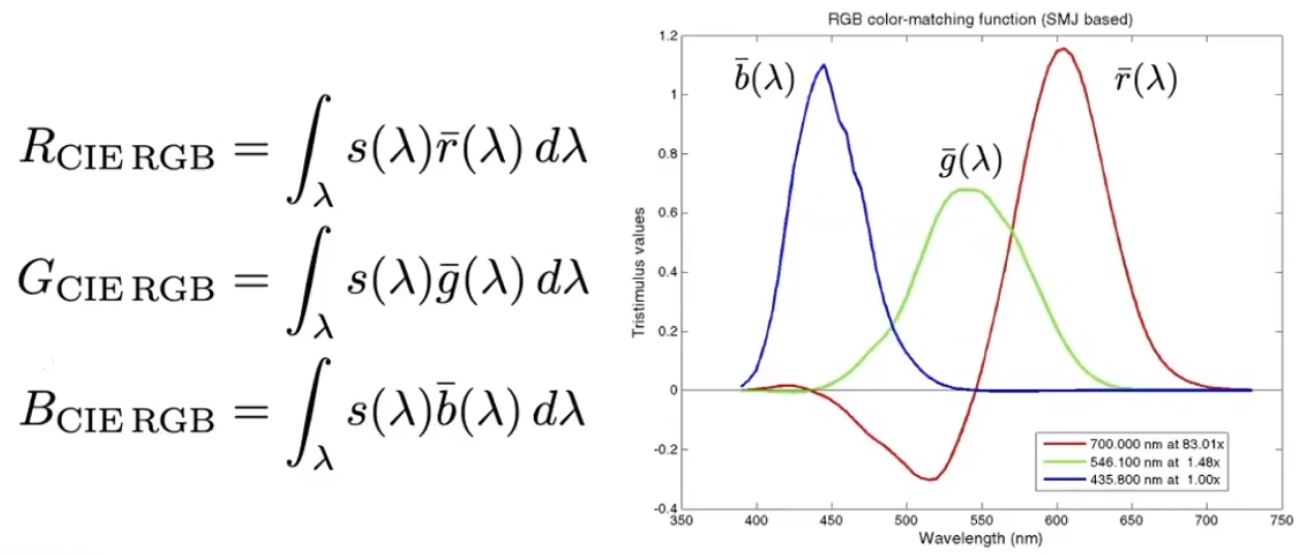
进而就可以得到三个积分结果 RGB ,以下公式仅供理解,并非推导方程:
# Color Spaces
# A Universal Color Space:CIE XYZ
- 定义好三个曲线 。并假定不同的波长可以按照曲线定义的比例进行混合后得到。
- 曲线 的分布比较均与,切覆盖整个波长,所以可以把 曲线视作亮度。
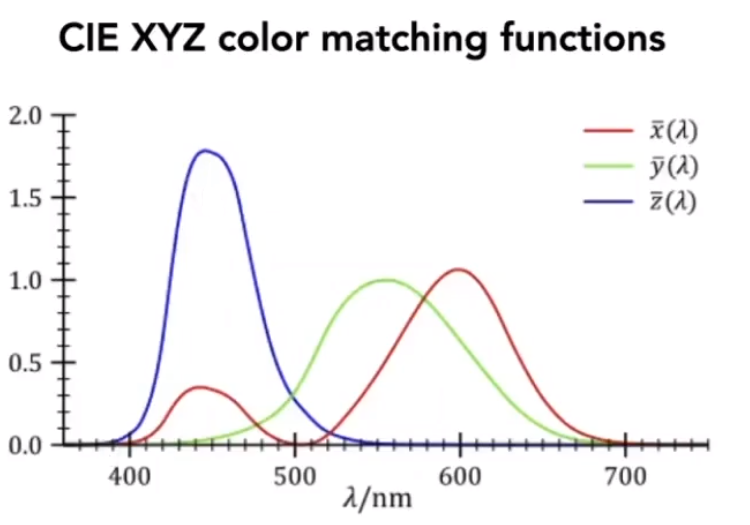
# Separating Luminance,Chromaticity
为了能够直观的表示一个二维的颜色域。对 ,进行归一化操作 ——$ x + y + z = 1$ 。
由于亮度不影响色域,所以假定 值恒定,那么就可以在变化 的情况下,绘制出 平面上的色域图。
# Gamut
这样就可以得到整个颜色空间内所有的颜色。
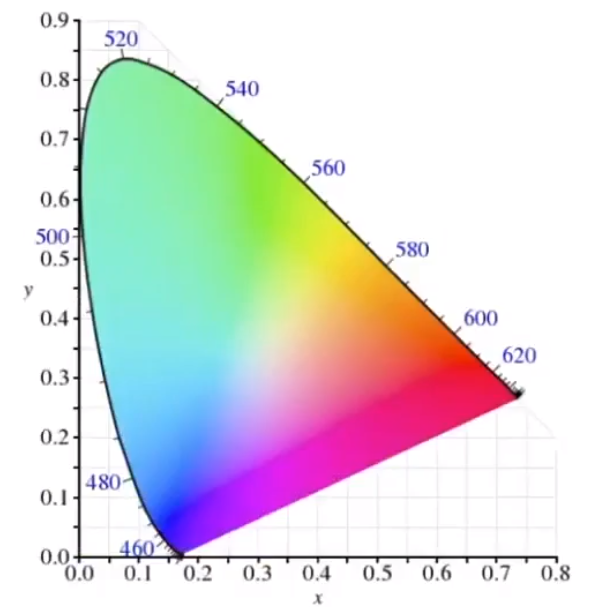
从下图可以看出,不同的表示方法所能表示的颜色范围是有限的。
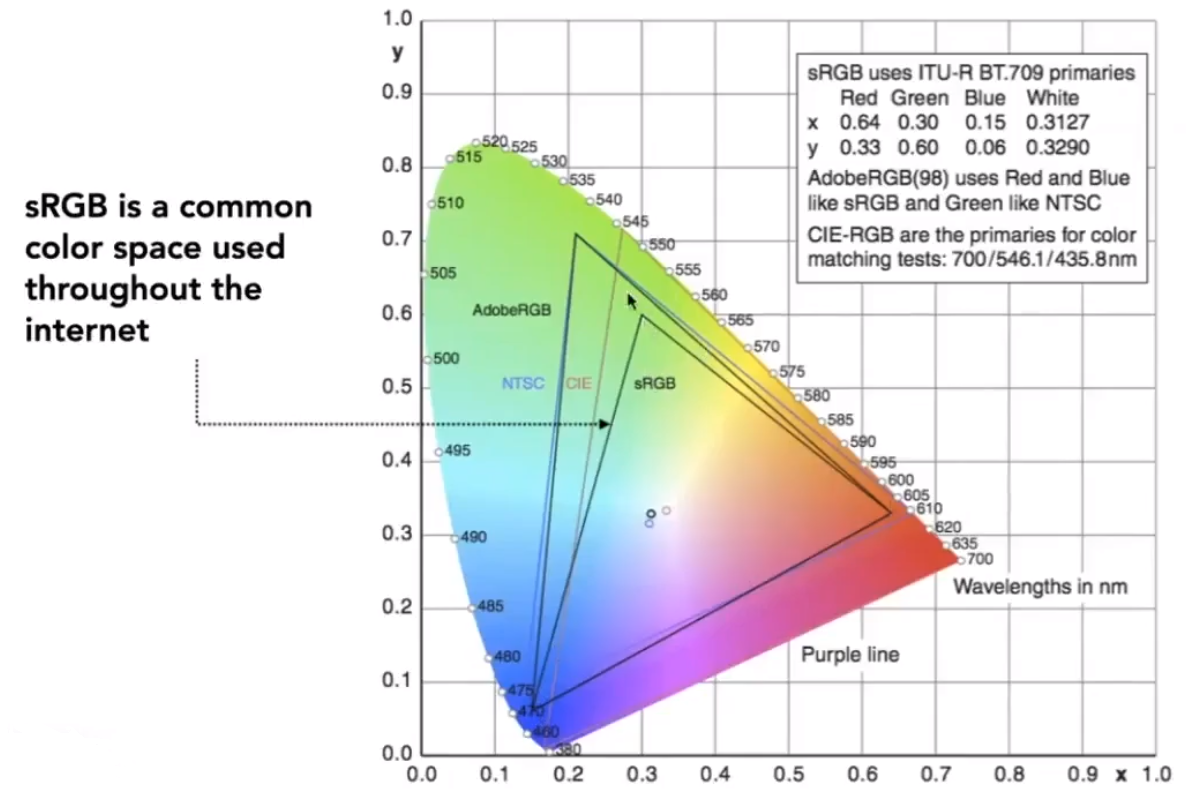
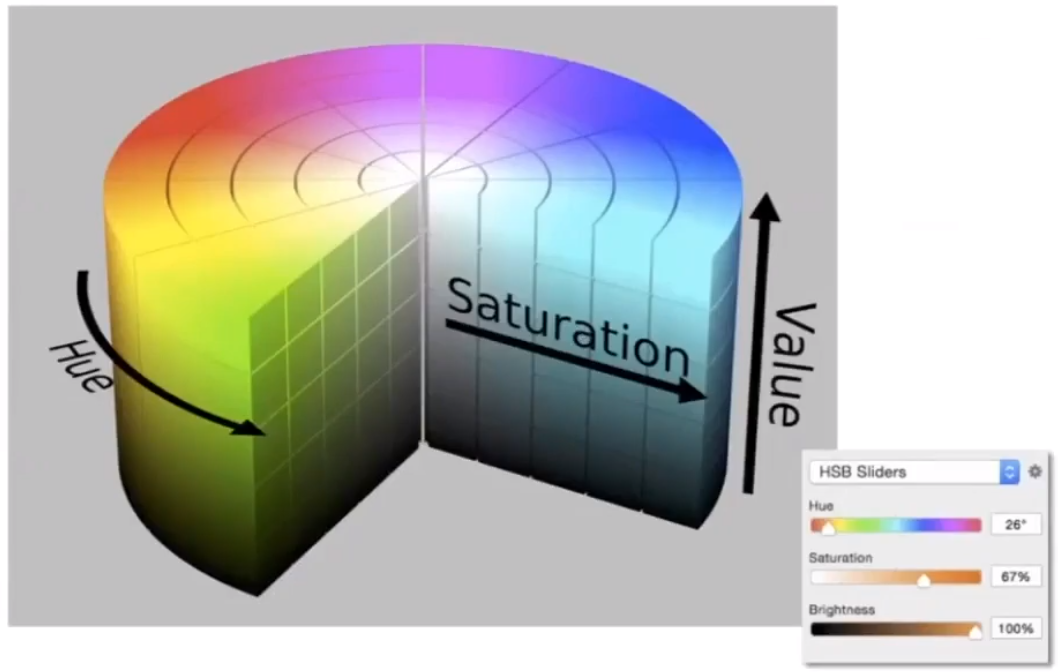
# HSV Color Space(Hue-Saturation-Value)
- H:定义颜色类型。
- S:定义颜色接近于白色程度。
- V:定义颜色的亮度。
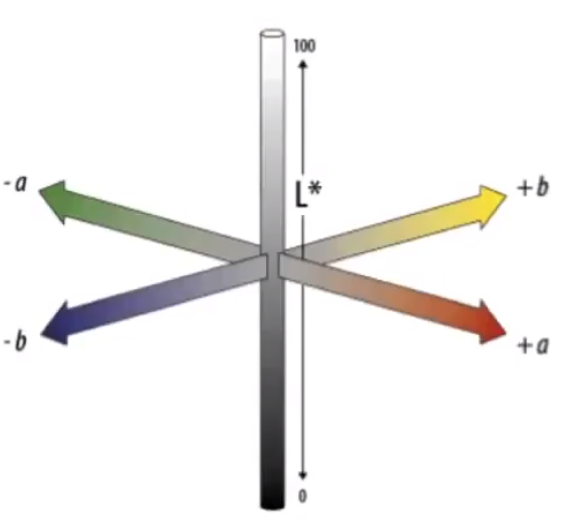
# CIELAB Space(AKA L*a*b*)
认为任意两个极端颜色之间互补。(白 - 黑,红 - 绿,黄 - 蓝)
- L* 表示亮度
- a * 表示红和绿
- b * 表示黄和蓝
# Additive Color
加色系统:不同颜色混合后,最终会变成白色。

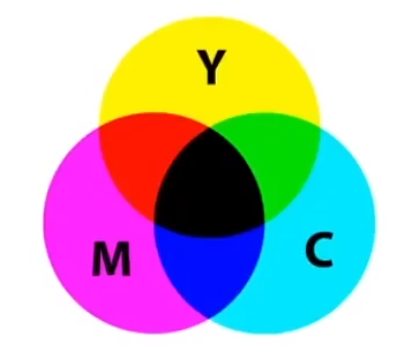
# CMYK:A Subtractive Color Space
减色系统:不同颜色混合后最终越来越接近黑色。
- C:Cyan
- M:Magenta
- Y:Yellow