以下为个人学习笔记整理,涉及坐标内容统一用右手坐标系,课程官网。
# Animation
# Keyframe Animation
给定了一个动画内几个比较关键的画面,从而推导出整个动画。
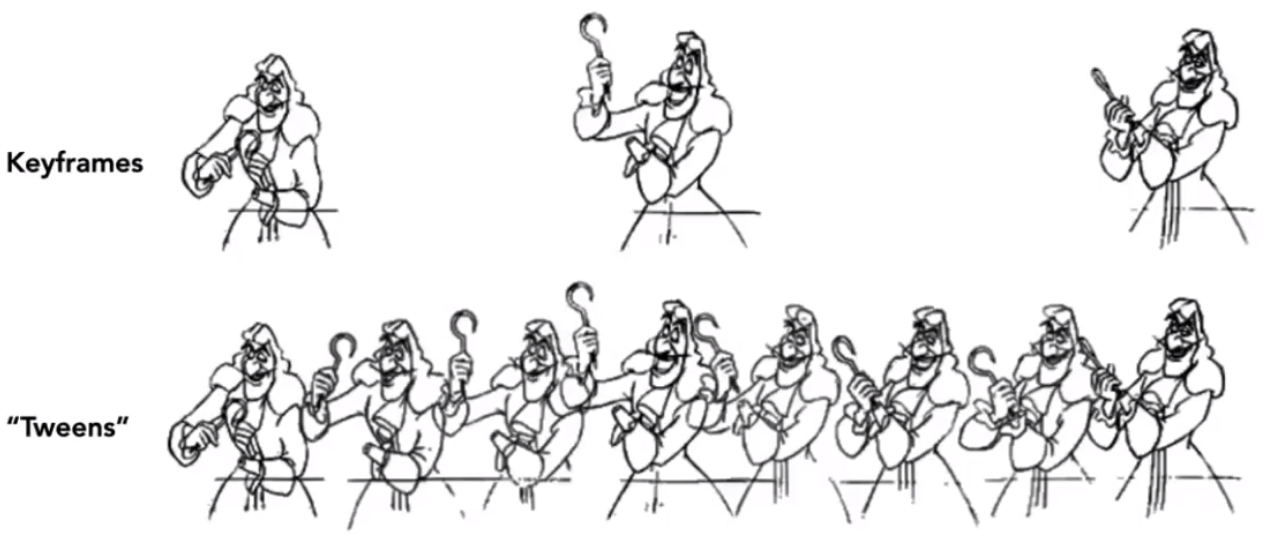
# Keyframe Interpolation
可以理解为,每个关键帧上有多个关键点,同一关键点在不同关键字的位置的插值,就能得到中间帧的关键点。
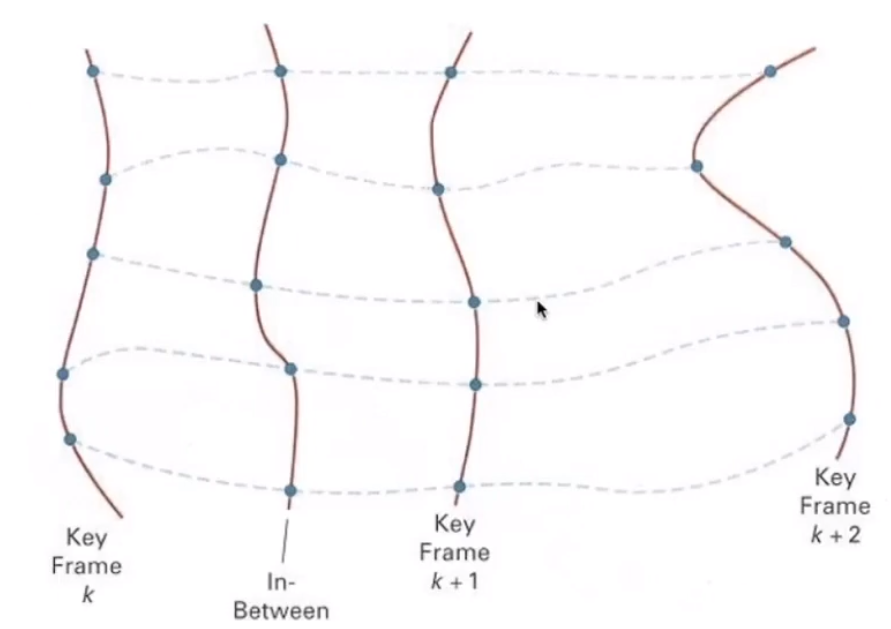
# Keyframe Interpolation of Each Parameter
因此,如何进行插值就是关键帧动画实现的核心。
- Linear interpolation:效果往往不是那么理想。
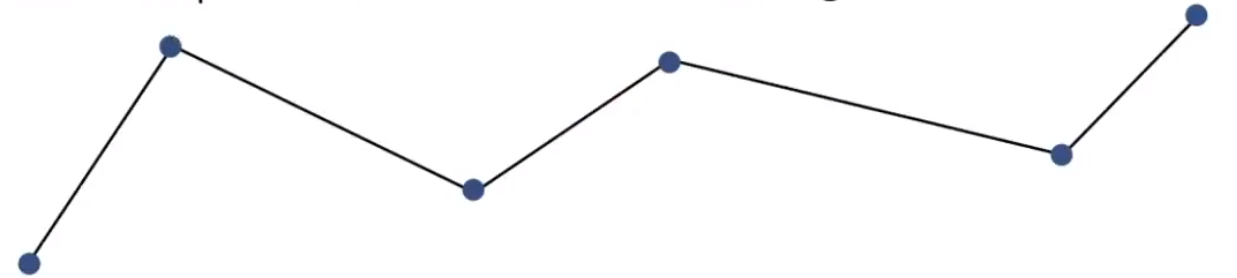
- Recall splines for smooth /controllable interpolation:追求线条的连续性。
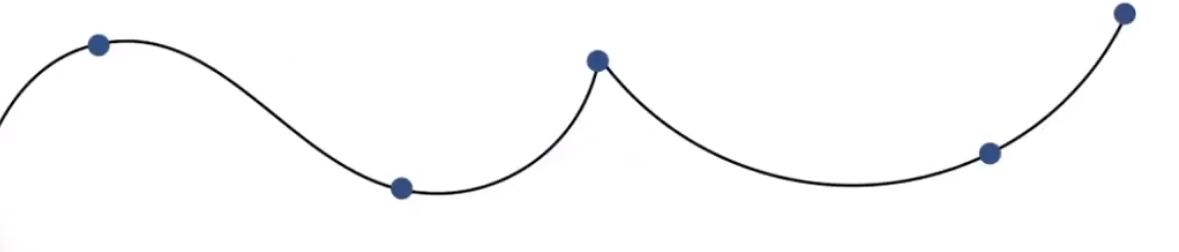
# Physical Simulation
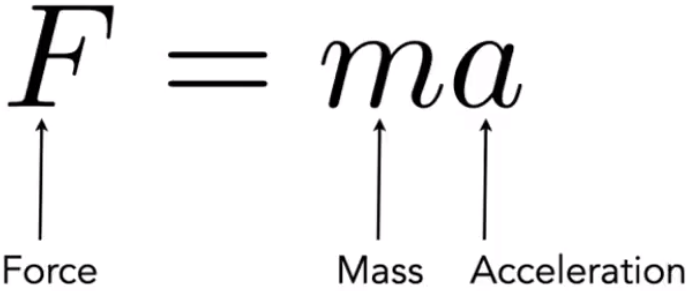
# Physical Based Animation
通过数值的模拟,来生成物体的运动。
# Mass Spring System
任何的物体都可以视为多个质点和弹簧相互连接的系统。
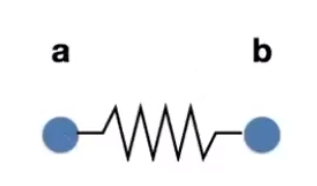
# Non-Zero Length Spring
没有弹簧初始长度为 0 ,这里需要定义一个初始长度
这里存在一个问题:能量没有消耗,弹簧会一直震动下去。
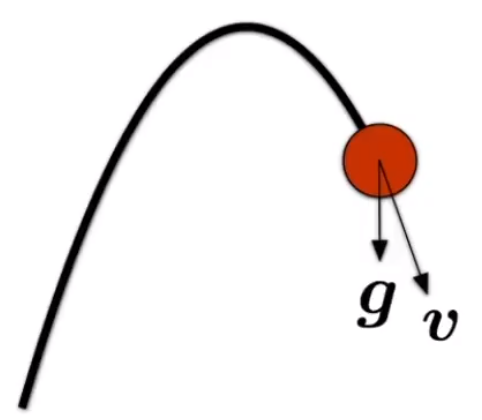
# Dot Notation for Derviatives
如果 是物体本身的位置,那么通常情况下会用 来表示速度向量 ,用 来表示加速度向量 。
# Introducing Energy Loss
为了能够使得弹簧停下来,引入一个能量损失。
这个力的目的是为了让物体能够停下来,所以力的方向是速度的反方向,并通过系数 控制大小。
这样,仍然会有一个问题:能量损失会导致,弹簧即使没有被拉伸,但是存在一个运动速度。最终也会因为能量损失这个问题导致停下来。因此,这个模型没办法很好的模拟弹簧内部的消耗。
# Internal Damping for Spring
引入弹簧的阻尼,用于描述弹簧内部之间作用力的消耗。考虑拉伸的情况下:
阻力方向和拉伸方向相反。 。
既然速度没办法描述弹簧内部的作用力,那么便引入弹簧两个质点的速度向量差来作为内部作用力。 。
然后对两者进行点乘投影,由于弹簧阻力方向只在 质点的连线方向,所以考虑阻力时也需要知道速度差在该方向上的投影值大小。
最终,在和阻力方向的单位向量相乘,就能得到最终的阻力向量(有大小,有方向)。
# 总结
最终,弹簧所受的力就等于:
- 和拉伸长度有关的反向作用力: 。
- 和弹簧本身阻尼有关的损耗阻力: 。
# Structures from Springs
通过多个质点和弹簧的模型,就可以模拟各种集合物体。
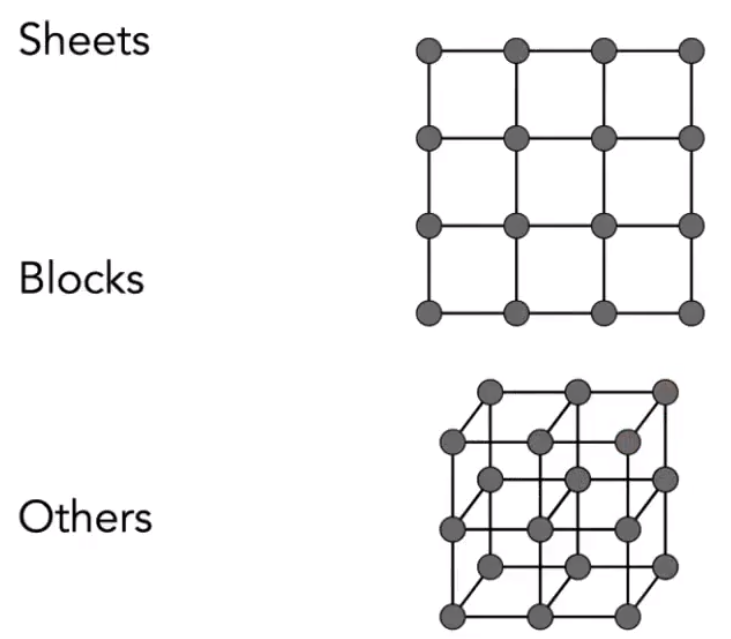
连接的方式,决定了结构的性质。
如果用如下方式模拟布料,会存在一些问题:
- 沿着对角线拉伸,会使得模型扭曲,并且不会回归远样。但实际情况下,布料并不会出现这种情况。
- 如果沿着对角线对折,也不会受到任何阻力。
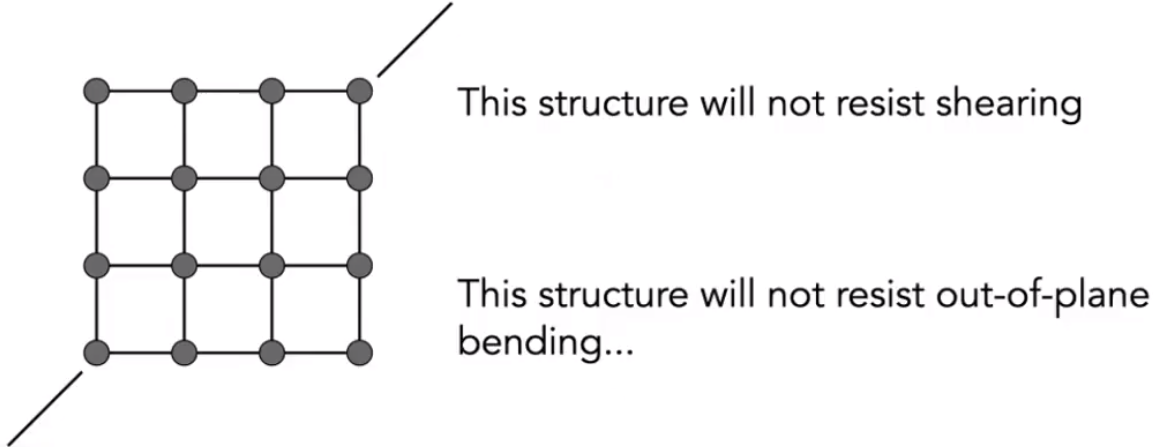
增加斜方向的弹簧,解决对角线拉伸问题。但是模型本身兑成了,且依旧没有解决对折问题🤒。
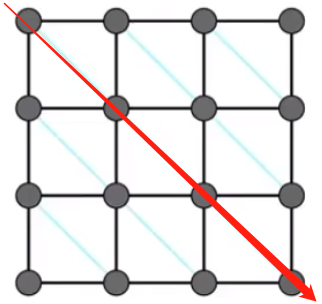
再引入另一个方向上的斜对角弹簧。虽然解决了对角线拉伸和对折,但对于水平或者数值的对折依旧存在问题🤔。
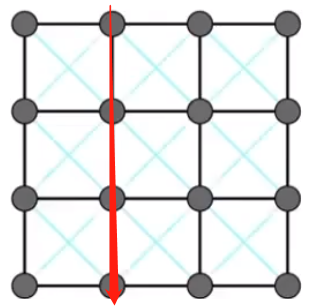
任意一个点和它相隔的点再引出一条连线。这下,模型看上去大致符合常理了😉🎉🎉🎉🎉,但离真正的布料还差的远呢(まだまだです)。
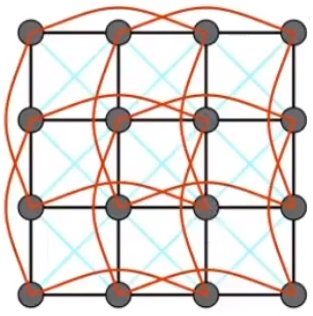
# Aside:FEM(Finite Element Method)Instead of Springs
类型模拟力从一个位置扩散到其他地方的方式,描述物体的运动。

# Particle Systems
用大量微笑的粒子集合来为物理系统进行建模。并且分析每个粒子的受力。

# Particle System Animation
实现粒子系统动画的步骤:
- 生成粒子
- 计算粒子的各种受力
- 根据受力更新粒子的速度
- 粒子销毁
- 渲染粒子
# Particle System Forces
- 引力和斥力
- 万有引力,电磁力
- 弹力,推力
- 阻力
- 摩擦力,粘力, 空间阻力
- 碰撞
- 墙壁,容器,固定物体
- 动态对象,角色身体
# Gravitational Attractoion
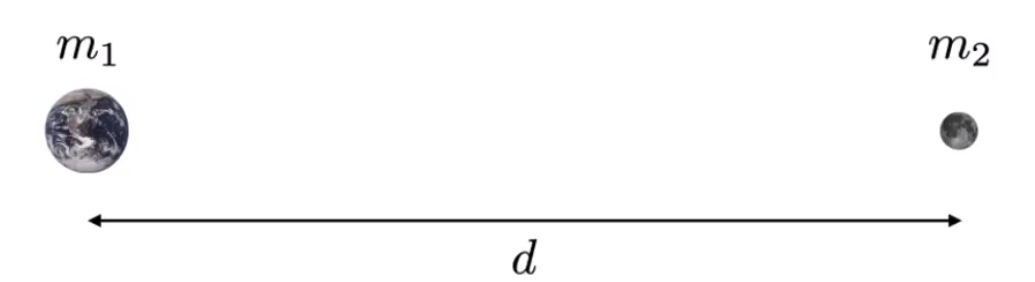
# Simulated Flocking as an ODE
例如通过粒子系统,模拟一个鸟群,根据鸟群的特点,总结出如下几个特性。
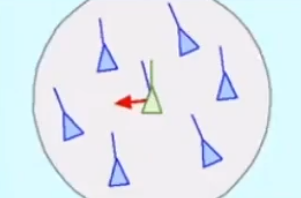
- attraction:任何单独个体的鸟,都希望能够进入鸟群的中心。
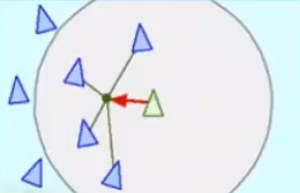
- repulsion:任何单独个体的鸟,有希望和其他同类保持一定的距离。
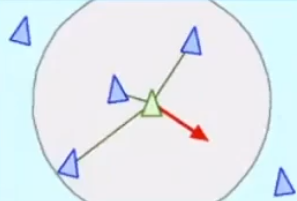
- alignment:任何单独个体的鸟,都会把偏向和同类一致的运动方向(轨迹)。
# Forward Kinematics
定义人体的运动方式。
- 拓扑结构(通过哪个关键)
- 关节的几何关系
- 树形结构(不含循环)
定义了几种关节的运动模式
- Pin:固定住的关节,只能绕着固定的点进行旋转(1D rotation)。
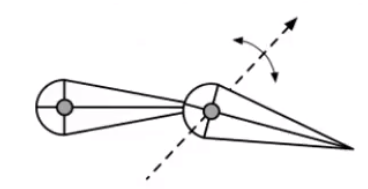
Ball:可以发生围绕某个点的旋转(2D rotation)。类似一个球在碗里的旋转。
Prismatic joint:出了旋转之外,还可以进行一些移动
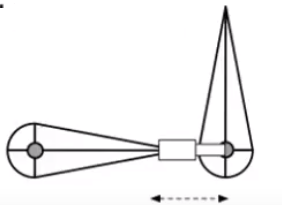
对一个关键末端求解:
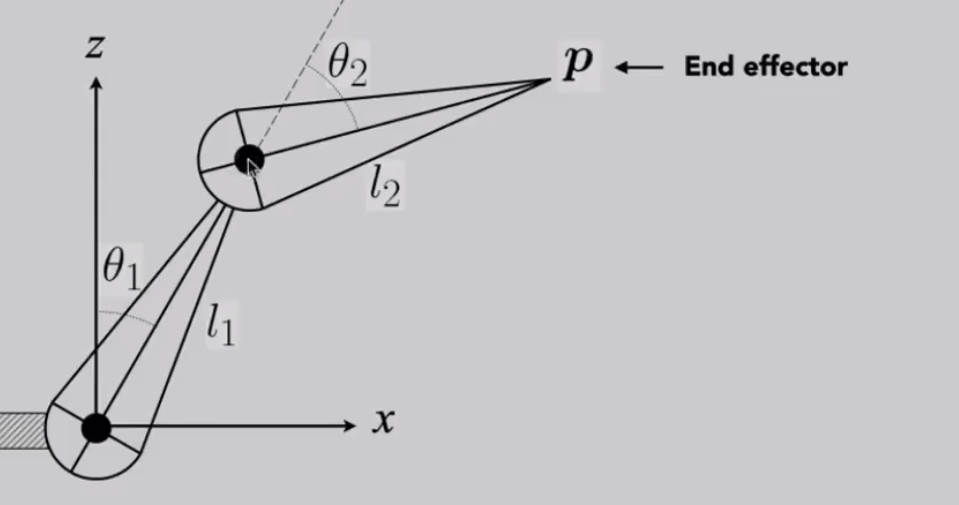
# Kinematics Pros and Cons
- 优点
- 控制直接方便
- 实现简单
- 缺点
- 动画效果不一定和物理一致时,该如何控制。
- 对于艺术家来说需要花费更多时间。
# Inverse Kinematics
并非定义每一个关键位置,最终实现控制末端位置的模式。
而是通过定义末端位置,从而推断出各个关节所需要的方向。
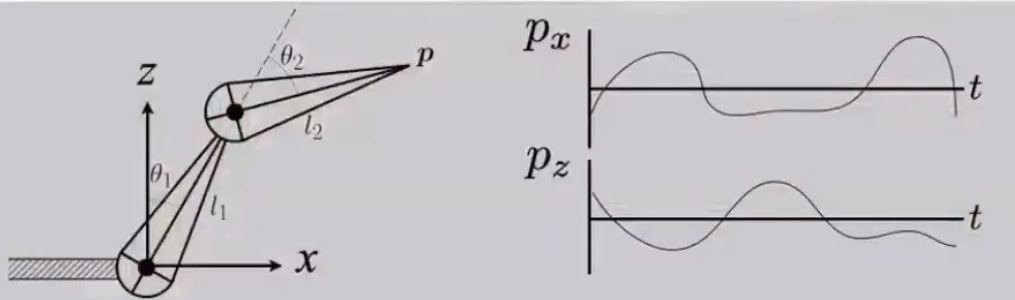
# Problem
- 逆运动学的解通常并不唯一。
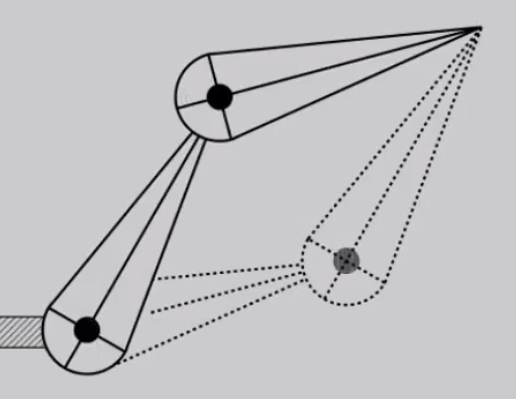
- 或者解压根就不存在。
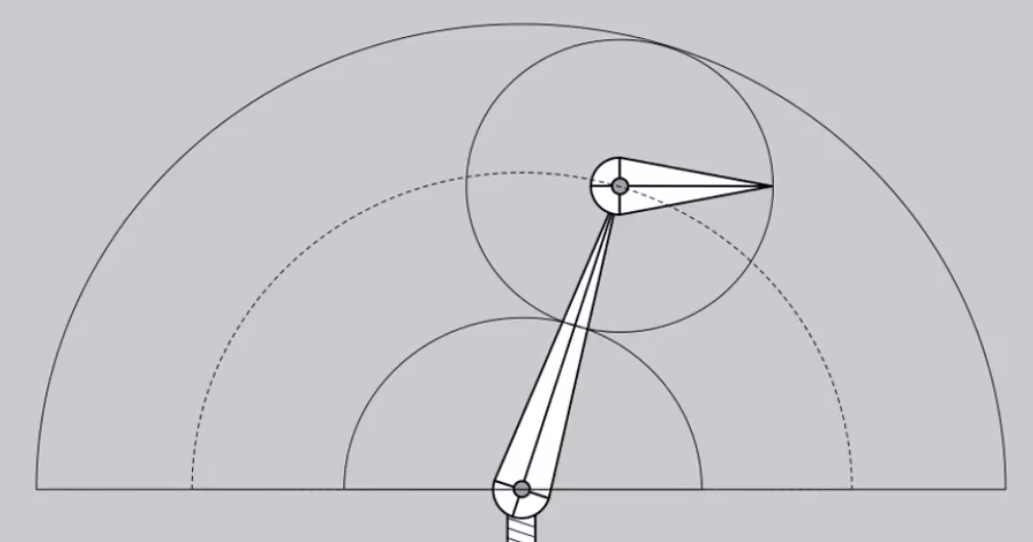
一种常规的解决办法是:通过类似梯度下降等算法,计算如何调整 能够让尖端逼近目标点。
# Rigging
定义了如何能够快速的操作角色,实现想要的姿态和效果。
就像木偶上的提线。

# Blend Shapes
定义两个关键位置,中间的状态通过类似插值的方式计算获得。


# Motion Capture
- 通过给真人打上各种关键点。
- 记录真实世界的运动状态。
- 运用到虚拟模型上。

# Motion Data
通过测量获得的一些数据 —— 各个控制点的运动轨迹。
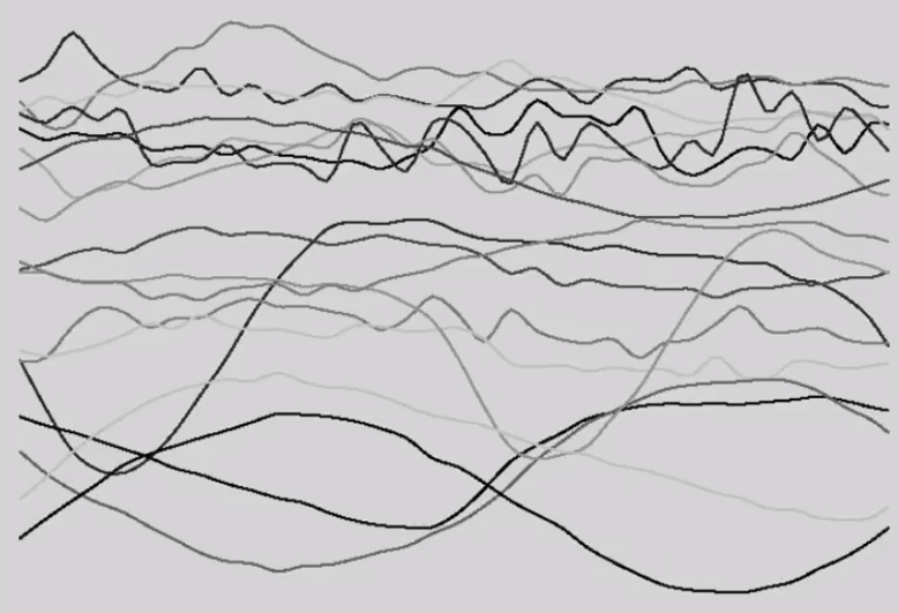
# Motion Capture Pros and Cons
- 好处:
- 能够快速获得大量的真实数据。
- 更加的逼真。
- 坏处:
- 设备复杂且昂贵。
- 动捕内容无法完全满足艺术家需要,需要后期调整。
# 关键字
- 常微分方程(ordinary differential equation)「ODE」:凡含有参数,未知函数和未知函数导数 (或微分) 的方程,称为微分方程,有时简称微方程 —— 来源百度百科
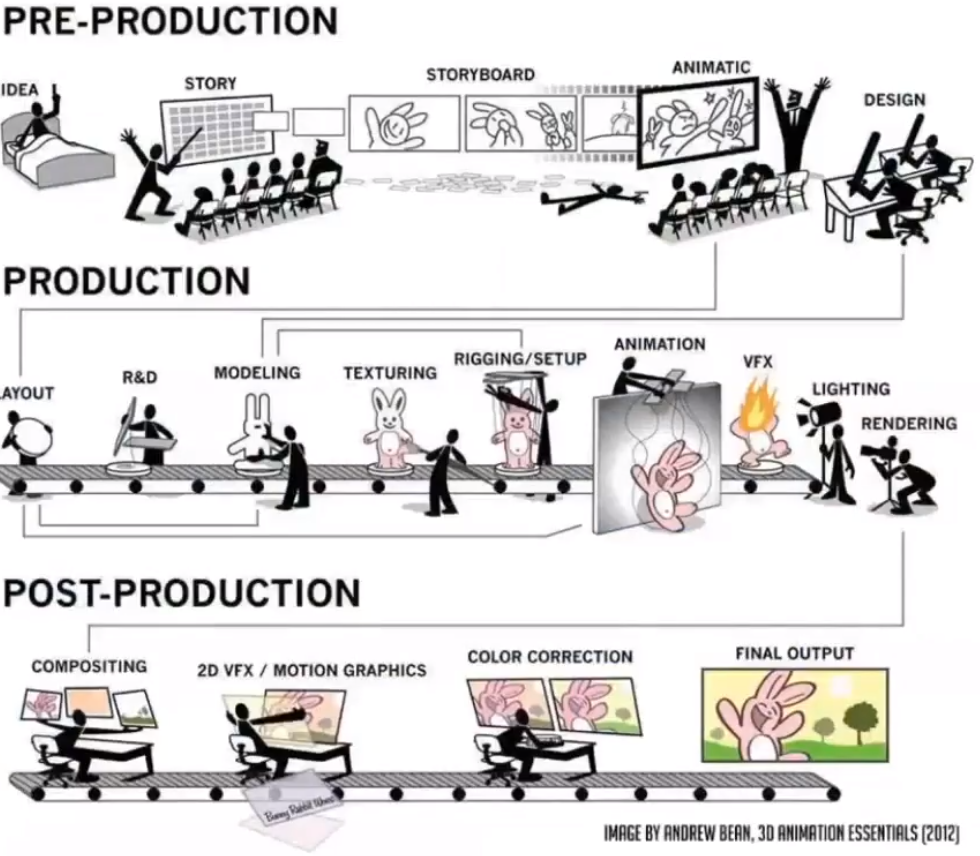
# The Production Pipeline
产品的完整流水线。