# Texture Mapping Cont

# 重心坐标（Barycentric Coordinates）

主要用来对三角形各顶点进行插值计算。

# 什么是重心坐标

在三角形 ABC 所形成的平面上的任何一个点，都可以用 A、B、C 三个顶点的线性组合。

如果该点在三角形内，那么 $\alpha , \beta , \gamma$ 都必须是非负的。

$$(x,y) = \alpha A + \beta B + \gamma C$$

$$\alpha + \beta + \gamma = 1$$

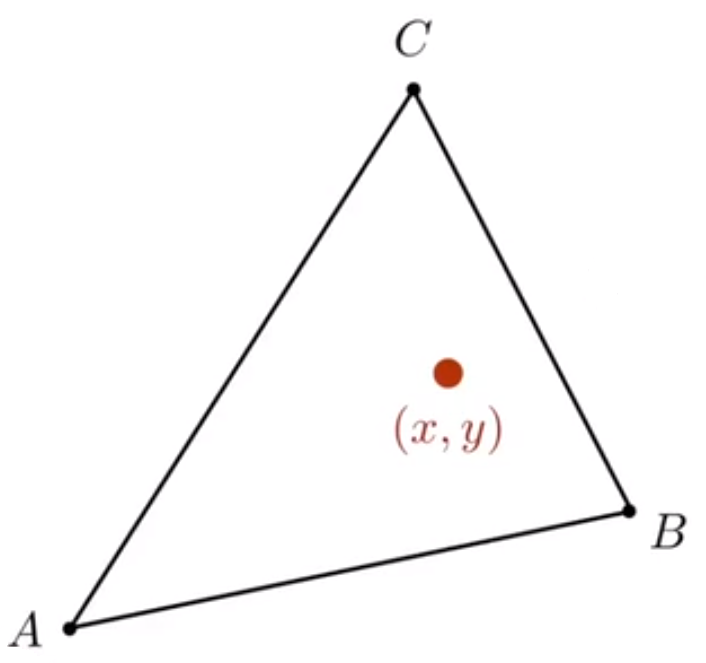
# 如何计算重心坐标

重心坐标和三角形各个边组成的三角形。各个三角形的面积除以三角形的总面积，就能得到前面的系数。

$$\alpha = \frac {A_A}{A_A+A_B+A_C}$$

$$\beta = \frac {A_B}{A_A+A_B+A_C}$$

$$\gamma = \frac {A_C}{A_A+A_B+A_C}$$

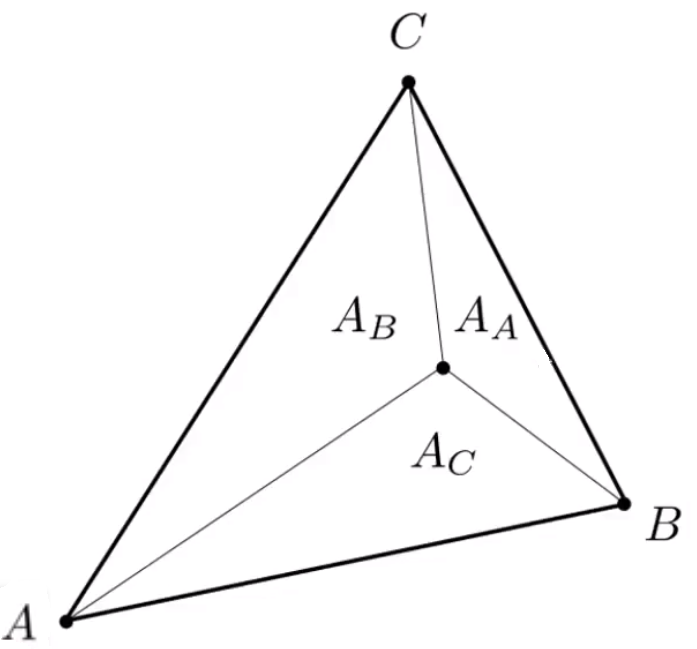
# 简化版本

去掉 $\gamma$ ，用 $\alpha,\beta$ 来代替。

$$\alpha = \frac{-(x-x_B)(y_C-y_B)+(y-y_B)(x_C-x_B)}{-(x_A-x_B)(y_C-y_B)+(y_A-y_B)(x_C-x_B)}$$

$$\beta = \frac{-(x-x_C)(y_A-y_C)+(y-y_C)(x_A-x_C)}{-(x_B-x_C)(y_A-y_C)+(y_B-y_C)(x_A-x_C)}$$

$$\gamma = 1 - \alpha - \beta$$

# 三角形的重心坐标在哪

当 $\alpha , \beta , \gamma$ 都等于 $\frac{1}{3}$ 时，组成的点，就是三角形的重心

$$(\alpha, \beta, \gamma) = (\frac{1}{3}, \frac{1}{3}, \frac{1}{3}) \quad \implies \quad (x,y) = \frac{1}{3}A + \frac{1}{3}B + \frac{1}{3}C$$

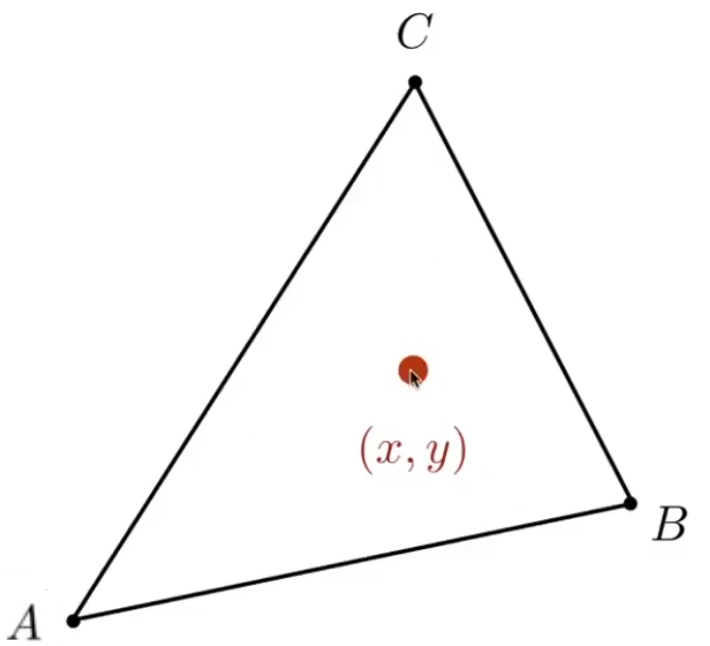
# 线性插值（Linearly interpolate）

针对任意的点 V 的颜色值，都可以用 $\alpha V_A + \beta V_B + \gamma V_C$ 来进行表示。

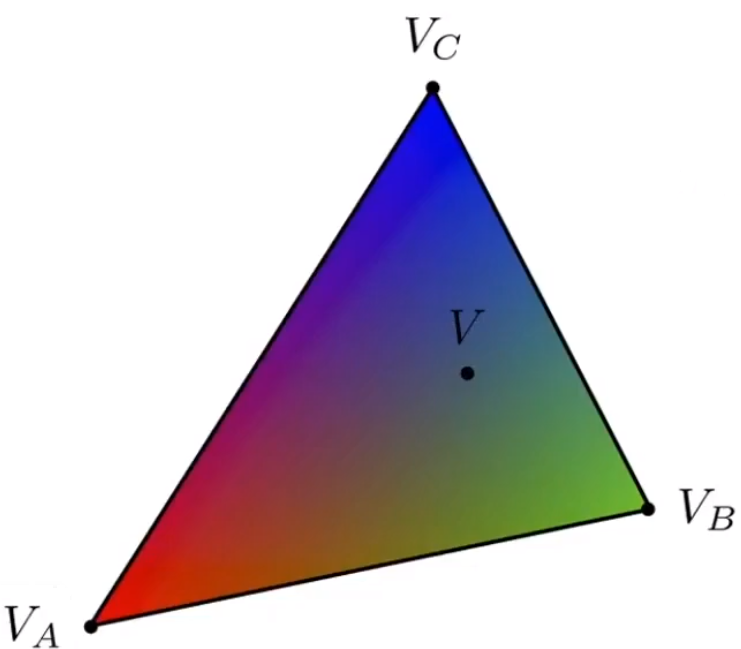
重心坐标在被投影之后，会发生改变 —— 投影前后的重心坐标不一致。所以做插值必须在投影之前（三维空间）做。

# 应用纹理

• 获取到三角形的重心坐标在投影后的坐标值 $(x,y)$。
• 根据重心和三角形顶点的插值，计算投影后的三角形内任意点对应的坐标$(x_u,y_v)$。
• 把投影后的坐标 $(x_u,y_v)$ 当作纹理的 $(u,v)$ 坐标进行采样。
• 得到的像素颜色，应用在该点的投影上（实际上就是应用在该点的漫反射系数 $k_d$ 上）。

# 纹理大小调整

# 纹理过小🔎

对于低分辨率的纹理应用在高分辨率的物体上，如何做才能实现高清效果。

# 取近似（Nearest）

对每个映射点四舍五入，会出现多个模型上的点，最终落在同一个纹理坐标上。

# 双线性插值（Bilinear）

针对纹理上的任意点，计算和它左下角和右上角纹理点的距离 $t,s$ ，这里假设每个纹理坐标的距离都是 1。然后对该点进行线性插值。

$$\text{线性插值:} \quad lerp(x,v_0,v_1) = v_0 + x(v_1 - v_0)$$

$$\text{双线性插值(水平):} \quad u_0 = lerp(s, u_{00}, u_{10}) \quad , \quad u_1 = lerp(s, u_{01}, u_{11})$$

$$\text{双线性插值(竖直):} \quad f(x,y) = lerp(t, u_0, u_1)$$

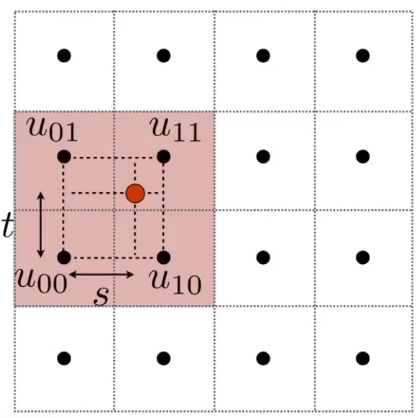
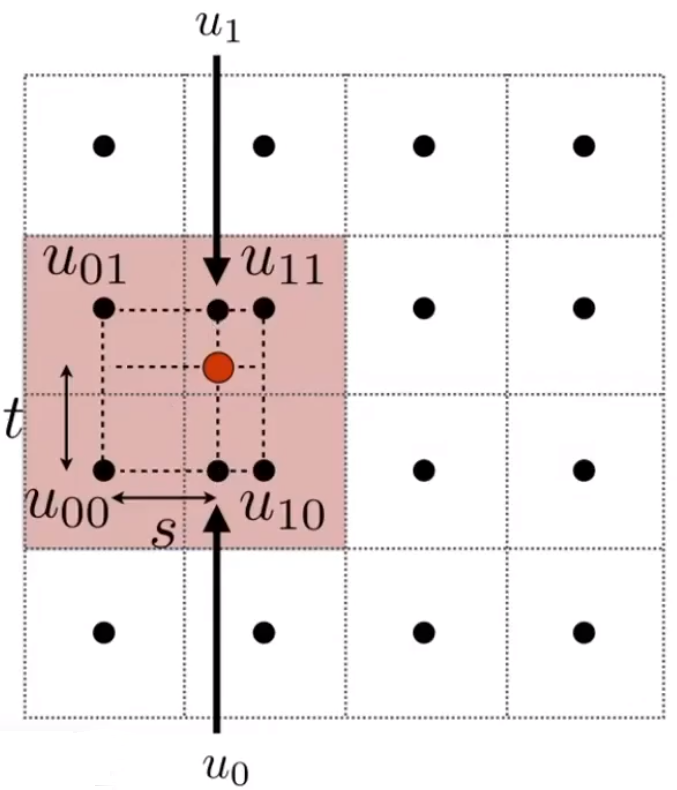
# 双向三次插值（Bicubic）

取周围临近的 16 个坐标，每次取四个点，做竖直和水平的插值，总共插值 3 次。

效果上是最好的，对于图像的边界，可以更加清晰的刻画。

# 纹理过大🔍

高分辨率的纹理贴图，应用在低分辨率的显示屏幕上：

• 摩尔纹
• 锯齿

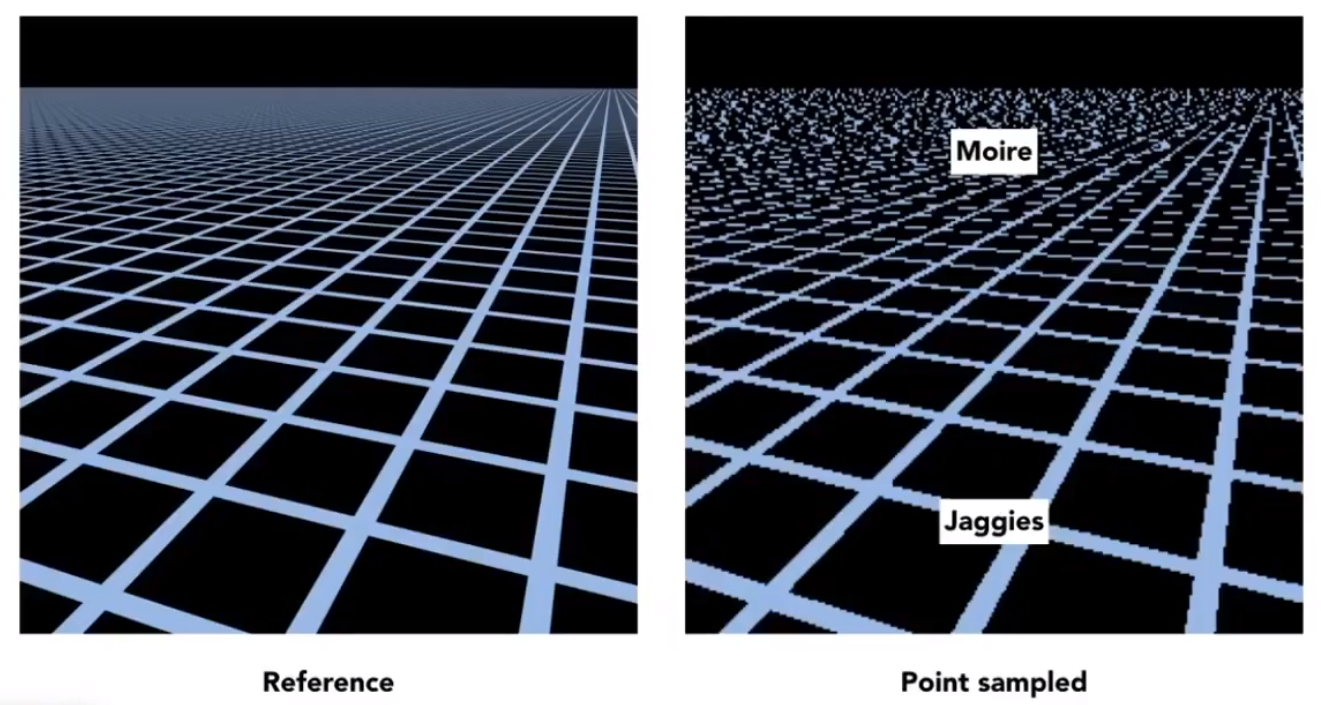
高精度纹理下，一个像素往往可能覆盖纹理上较大一块区域。

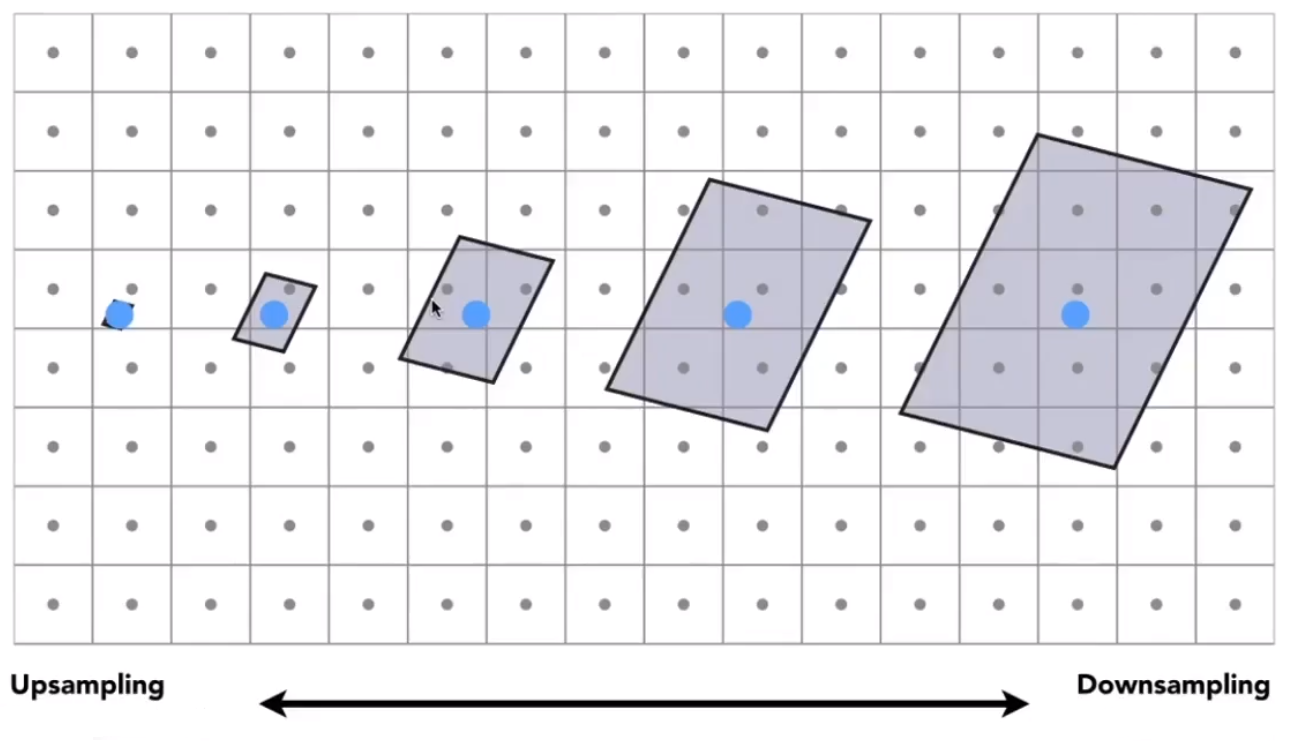
# 超级采样（Supersampling）

能行，但是太耗。

• 在一个像素内进行多个区域的采样，并进行平均

# Mipmap——multum in parvo map

用来进行范围查询，获得某点的像素平均值。根据不同的精度，选择不同的层级进行采样。

• 效率高
• 不准确
• 纹理只能是正方形

每一层比上一层的总像素缩小 $\frac{1}{4}$ 。最终的总大小，比原来多出 $\frac{1}{3}$ 。

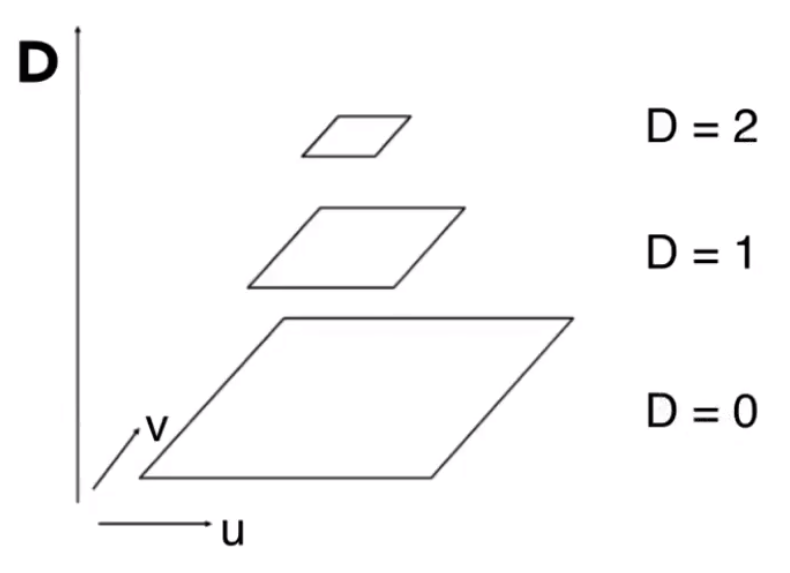
# 如何知道该选择哪一层❓

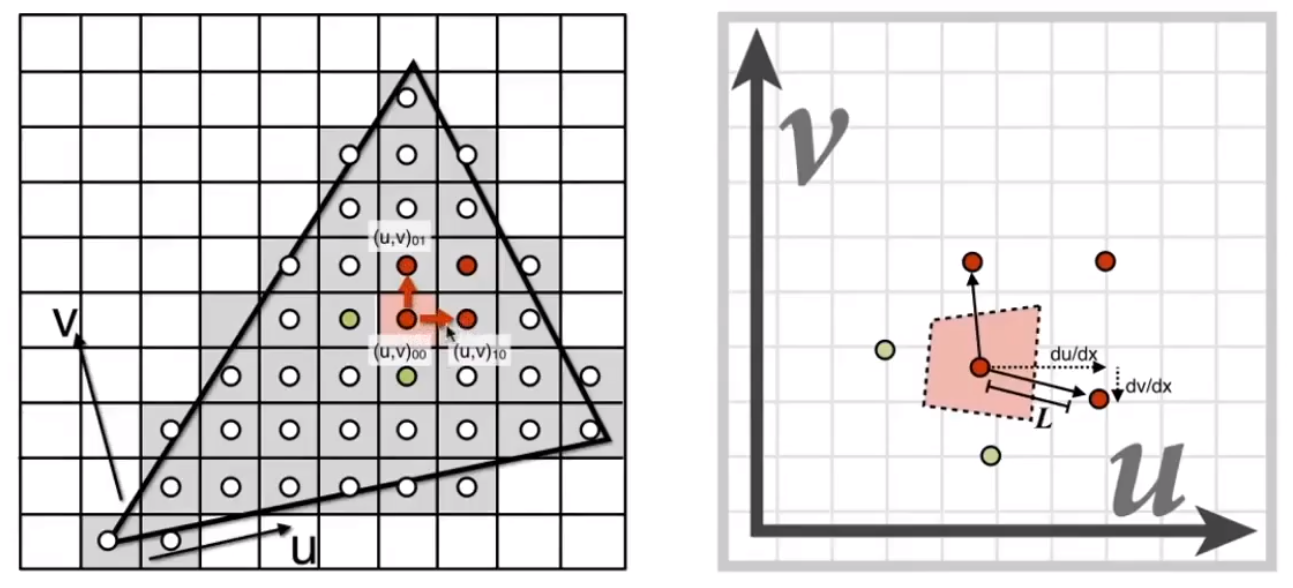
计算屏幕上的一个点，移动一个单位距离。需要纹理上该点移动多长距离。计算 $u,v$ 两个方向的最大值。

最终就可以知道在 D 层上，屏幕上的一个单位距离，和纹理上的一个单位距离最为近似。

$$D = {log_2}L \quad , \quad L = max \begin{pmatrix} \sqrt{ {(\frac{du}{dx})}^2 + {(\frac{dv}{dx})}^2 }, \sqrt{ {(\frac{du}{dy})}^2 + {(\frac{dv}{dy})}^2 } \end{pmatrix}$$

最终的结果，各个层级之间的区分会非常的明显。这样得到的效果不会太好。

# 三线性插值（Trilinear）

大部分的游戏内，用的都是「三线性插值」，效果好，过渡连续，也不太耗。

• 先分别在两个近似层级上做「双线性插值」。
• 再对两个「双线性插值」的结果，进行层级间的插值。

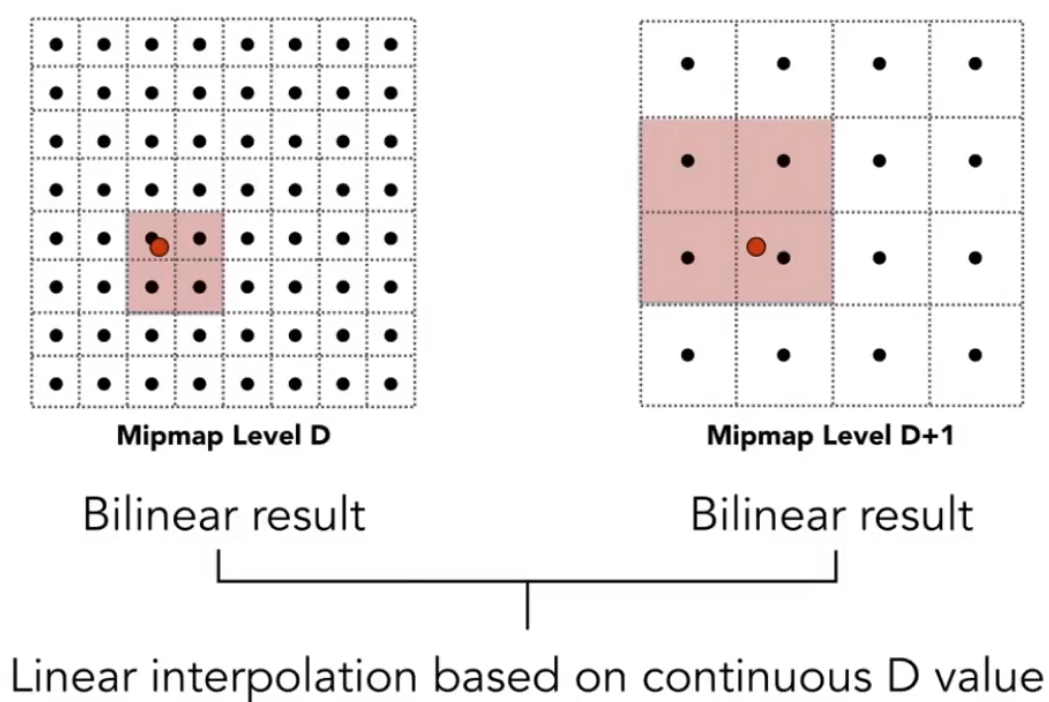
三线性插值的最终效果

# 过模糊（Overblur）

Mipmap 虽然效果不错，但是在有些情况下，会出现过模糊的效果。可以使用 「各项异性过滤」来解决。

# 各项异性过滤（Anisotropic Filtering）

Mipmap 之所以会出现过模糊。是因为 Mipmap 只能处理正方形的纹理，对于长方形的图片，处理起来效果就没有那么的理想。

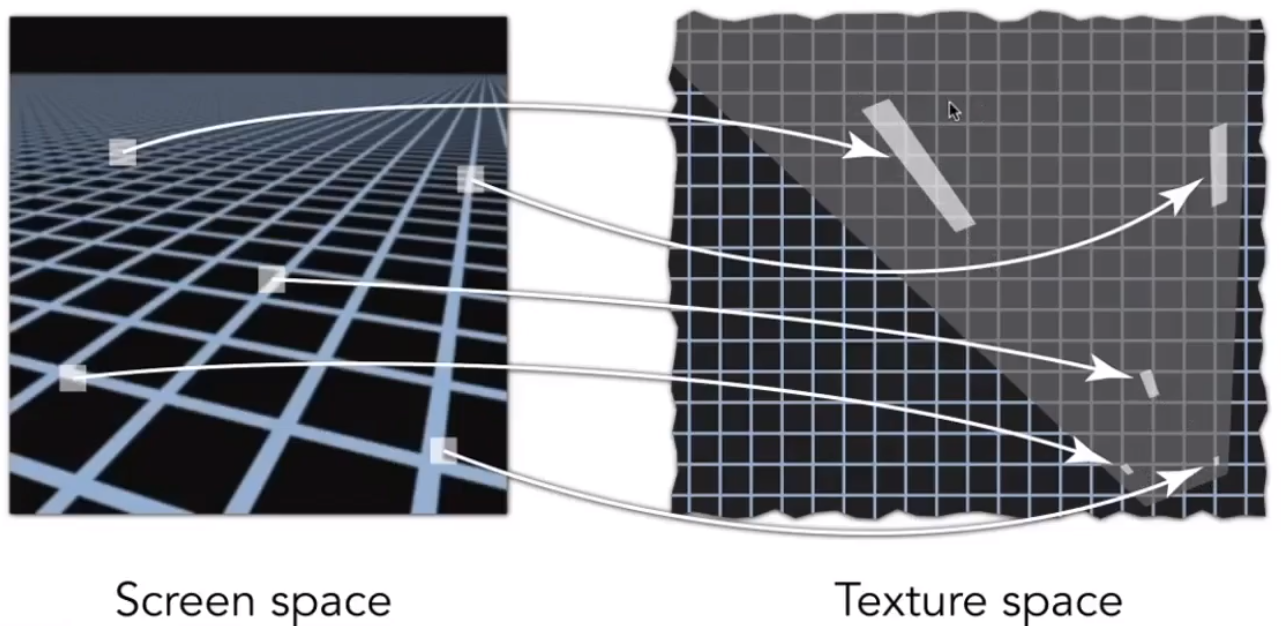
所以，针对不同的矩形，分别得到它不同长宽比的图片可以解决该问题。但是，对于斜着的矩形，或者其他不规则的图形，效果就不太理想。

总图像大小也变为了原来的 3 倍。

# 纹理应用（Applications of Textures）

# 环境贴图（Environment Map）

通过贴图的形式，实现环境光的镜面效果

这里假设的环境光贴图，只保留了环境光的方向，没有考虑物体和观察点的距离。

存储环境光的办法：环境光先投影在一个金属球面上的影像，可以视作是这个环境所形成的环境光图像。

把环境光记录在球面上，被称之为「球形贴图（Spherical Map）」。

# 球形贴图的问题

球形贴图的顶部和底部展开后会出现一定程度的扭曲。

# 使用「天空盒（Cube Map）」可以解决这个问题

假设从球心发射一条条的光速，把球面上的像素投影到立方体的各个面上。

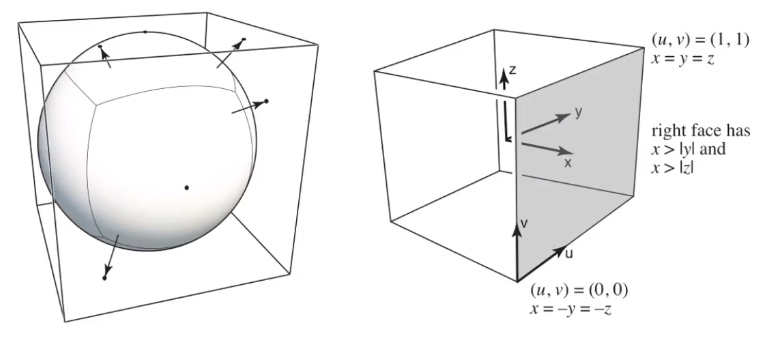
投影之后就可以得到六个面的图像。

# 法线贴图（Normal map）

用纹理贴图来表示法线，伪造物体的深度，实现阴影效果。

不对几何物体的形状做任何的改动，只修改物体表面的「相对高度」，进而改变法线方向。

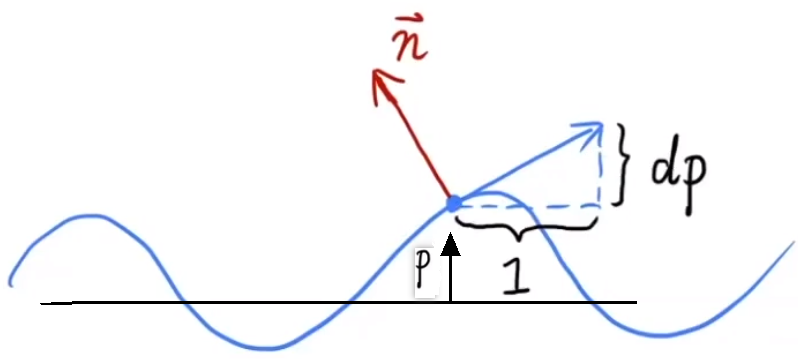
# 如何通过高度差计算法线方向❓

# 计算二维空间

• 假设物体原本是水平的，那么物体上各个点的法线 。$n(p) = (0, 1)$
• 通过该点的高度值，计算出水平切线的方向，可以视为该点水平移动一个单位的高度变化乘上一个贴图的影响权重。 $c \times(h(p+1) - h(p))$
• 通过切线方向，计算法线方向。$(-dp, 1).normalized()$
  • 切线的向量表示：$(1, dp)$
  • 法线的向量表示：$\vec n = (-dp, 1)$

# 计算三维空间

• 假设物体原本是水平的，那么物体上各个点的法线 。$n(p) = (0, 0, 1)$
• 计算纹理 $u,v$ 方向的切线。
  • $dp/du = c1 \times (h(u+1) - h(u))$
  • $dp/dv = c2 \times (h(v+1) - h(v))$
• 通过切线方向，计算法线方向。$\vec n = (-dp/du, -dp/dv, 1).normalized()$

这里使用的坐标系都是局部坐标，可以简单的把原法线统一视为 $(0,0,1)$。得到法线贴图的法线方向。之后再把坐标转为世界坐标。

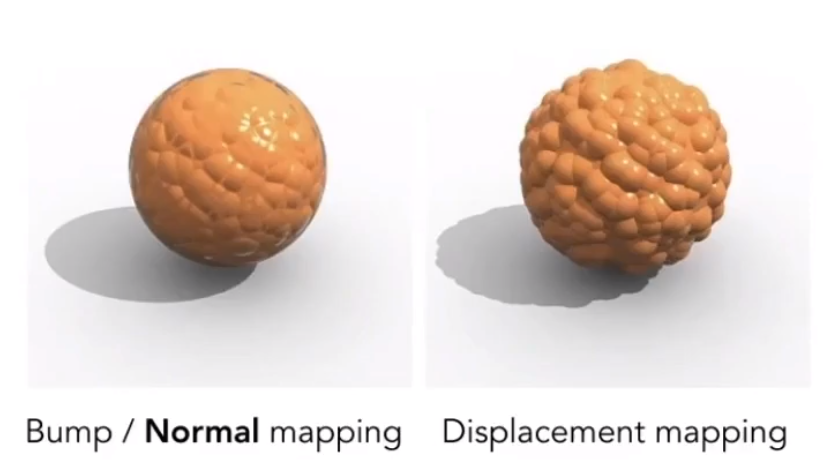
# 位移贴图（Displacement map）

相比于法线贴图对于物体表面的法线进行修改，从而影响光照。位移贴图则是直接对顶点的坐标进行修改，模拟更加真实的效果。

位移贴图由于是改变三角形顶点的位置，所以其对于模型顶点精度有着一定的要求。

通过物体的阴影就能很容易的分别出两者的区别

# 3D Procedural Noise

通过三维空间的噪声函数，定义三维空间内每个点的纹理，并非只局限于物体表面。

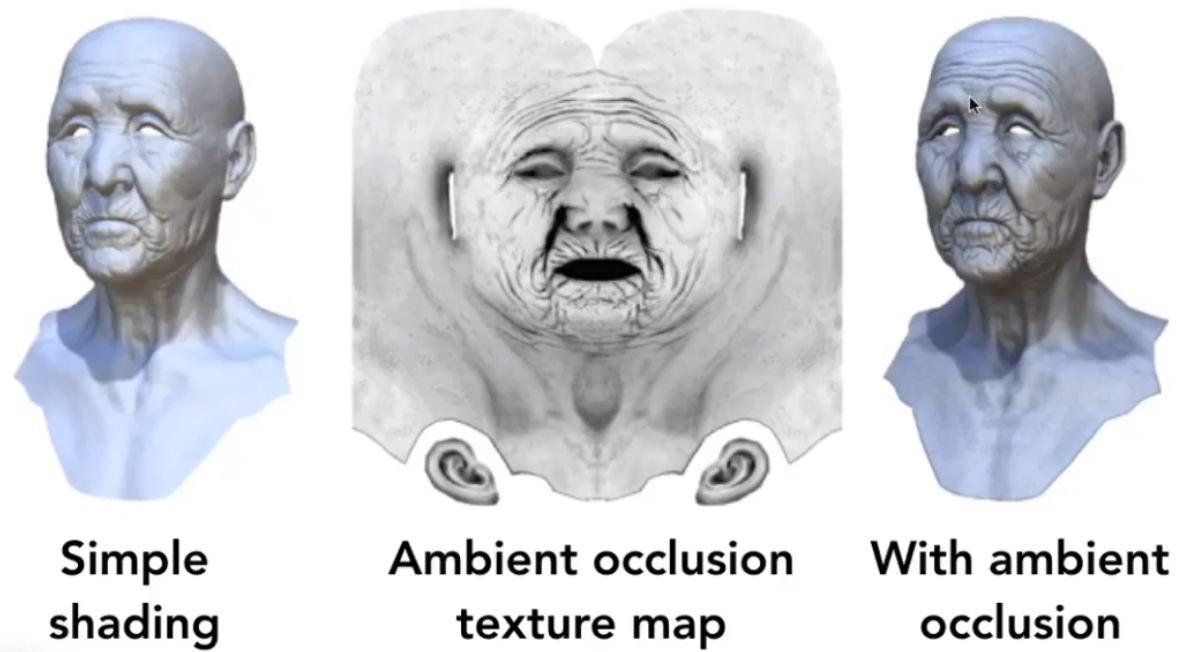
# 阴影贴图 (Shading map)

预先计算好物体的阴影，并提前应用在纹理贴图上，有点类似于烘培的效果

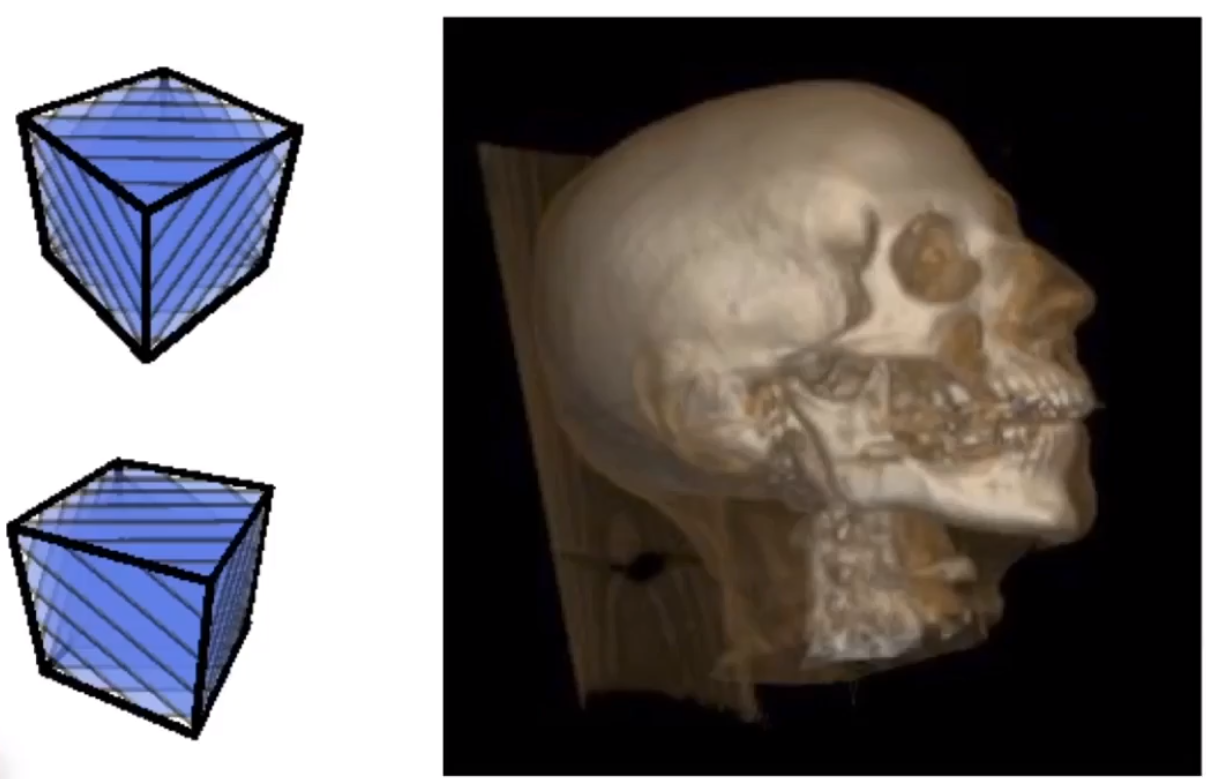
# 3D 纹理和体积渲染（3D Textures and Volume Rendering）

不仅仅用于绘制物体表面，而是在 3 维空间内记录每个点的纹理。

# 关键字

• 动态曲面细分：在低精度的模型上应用位移贴图时，根据实际情况对模型进行高精度处理（一个三角形，拆分成多个小三角形）