以下为个人学习笔记整理,涉及坐标内容统一用右手坐标系,课程官网。
# 着色(Shading)
对不同物体,应用不同材质(material),这里暂时不考虑物体的阴影。
# 冯氏光照(Blinn-Phong)
高光(Specular highlights)
漫反射(Diffuse reflection)
环境光照(Ambient lighting)

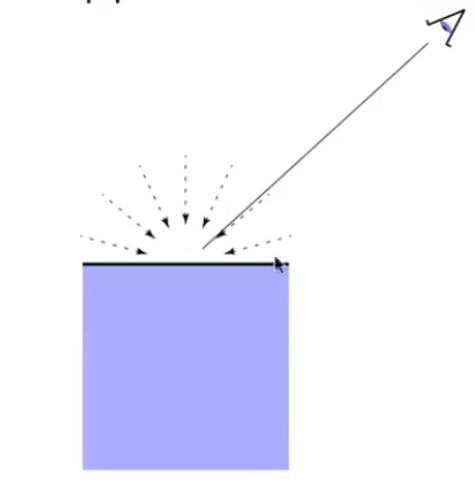
# 漫反射(Diffuse reflection)
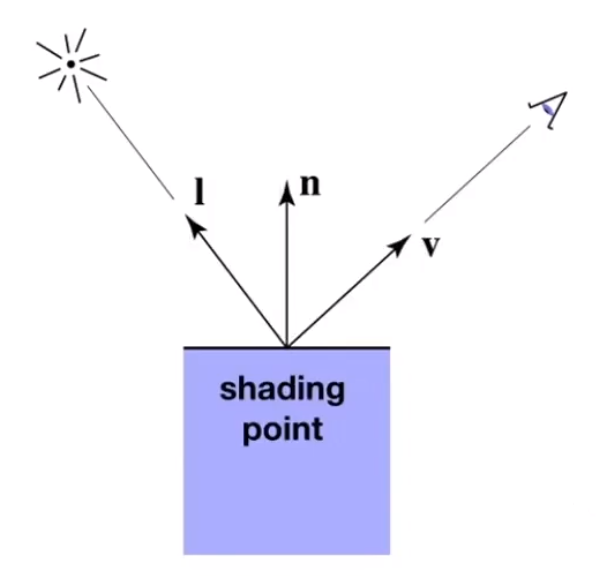
# Shading point
- 视野方向(View direction)
- 物体表面法线(Surface normal)
- 光照方向(Light direction)
- 物体表面参数(Surface parameters)
- 颜色
- 亮度
- ...
# 角度和光线强度的关系
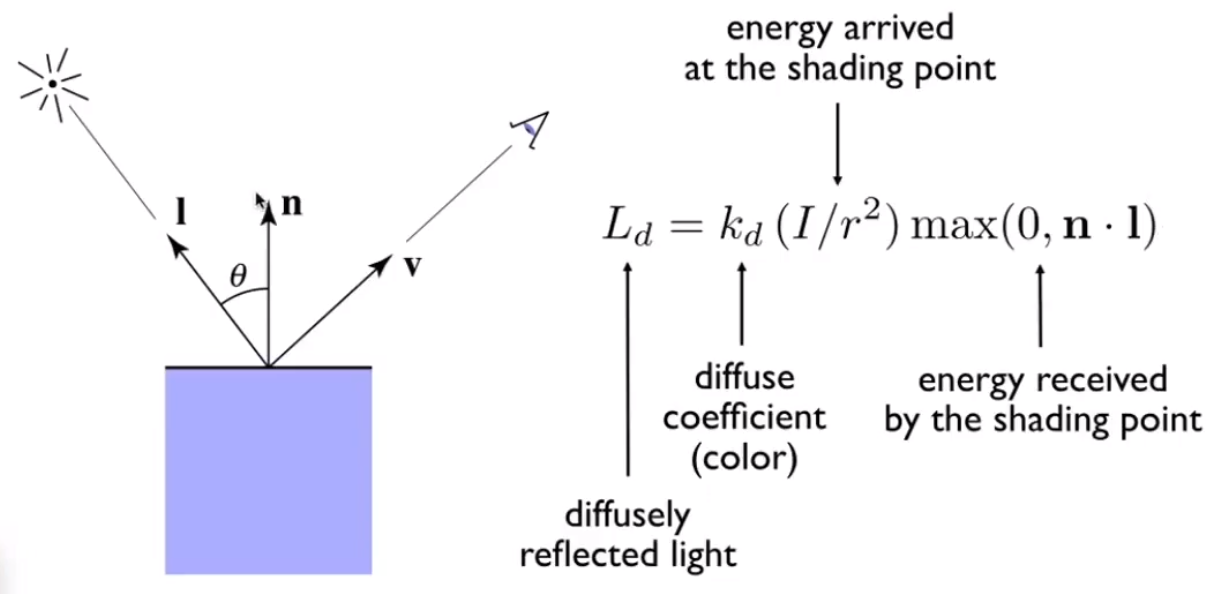
不同角度的光线,明暗不一样。物体表面的光线和物体表面的法线夹角决定亮度 。

# 距离和光线强度的关系
假设能量在传播过程中不会减少,假设半径为 1 的球表面上某个点的能量为 ,那么通过计算,得到半径为 的球上的能量就是 。

# 光线强度的最终结果
- :表示材质表面的漫反射系数。
- :表示距离对光照强度的影响。(这里的 考虑的是光源和物体的距离)
- :表示光线本身和法线的夹角,影响光照的强度。(不考虑 为负数的情况)
- 漫反射不需要考虑观察者的视角 。

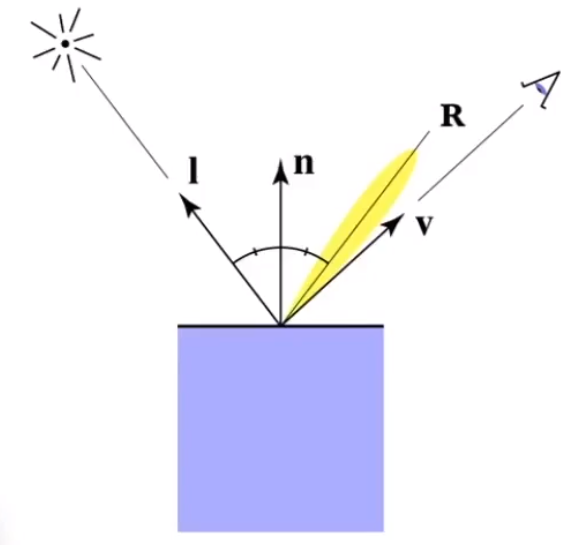
# 高光(Specual)
高光更近似于镜面光,只能在某些特定的位置,才能观察到。所以也可以理解为,光线的镜面反射方向和观察方向越接近,高光越明显。
为了便于计算,一般情况下会用半程向量和法线的夹角 来计算,而半程向量又可以通过三角形法则通过简单的向量加法得到。
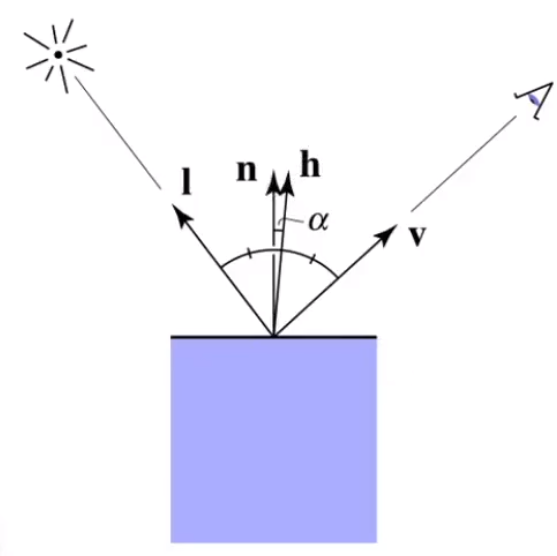
# 高光光照公式
高光反射里没有考虑角度变化对于光线的衰减 。实际生活中,这是需要的。
# 为什么 需要指数 p ❓
对于常规的 , 的角度就算很小的时候,依旧能够产生不错的高光效果,但这和实际的效果不符合。
例如 角度在 时, 的值会很大,超过 ,但实际情况并非如此。而 的 角度在 左右就看不见高光了,比较符合现实。

Blinn-Phong 模型下的指数 通常在 之间。通常情况下 角度在 就看不见高光了。
# 不同指数 和 镜面反射系数 下的高光效果。

# 环境光照(Ambient)
由于环境光是物体之间,经过多次漫反射或者镜面反射,最终到达人眼的光线,所以环境光的分析较为复杂。
# 环境光公式
由于环境光较为复杂,索性假设任何一个点的环境光强度都是相同的。不考虑光照方向和观察方向。
# 最终的光照公式
所有种类的光照进行叠加
