以下为个人学习笔记整理。组内分享文档
# JPS 算法分享
# 介绍
JPS 又名跳点搜索算法(Jump Point Search),是由澳大利亚两位教授于 2011 年提出的基于 Grid 格子的寻路算法。 JPS 算法在保留 A* 算法的框架的同时,进一步优化了 A* 算法寻找后继节点的操作。
# A * 算法
由于 JPS 的实现是基于 A* 算法的基础上完成的。因此,让我们简单回顾一下 A* 算法:
# 算法核心
# 数据结构
open_map:待遍历字典,存储需要遍历的节点。close_map:已遍历字典,存储已经遍历过的节点。p_queue:优先队列,底层实现二叉堆。point:节点,存储内容:- 距离终点距离
h(n) - 距离起点距离
g(n) - 父节点。
- 距离终点距离
# 算法过程
起点加入 open_map | |
起点加入 p_queue | |
while p_queue 不为空: | |
弹出优先级最高的节点 | |
把周围八个节点加入待遍历节点 | |
已经存在于 open_map 的节点更新距离和父节点信息 | |
已经存在于 close_map 跳过 | |
遇到终点终止循环 |
# 优先级比较
优先级比较遵循以下公式
即:起点到该节点的距离 + 该点到终点距离和最小的节点优先级最高。
由于估计函数 h(n) 有很多种,展开讲将会耗费较大篇幅,本文主要以「 欧几里得距离(两点直线距离)」作为 h(n) 和 g(n) 的计算基础
# 其他前提条件
方便后续测试统一,地图大小采用 20 x 20 的方格。
运动路径支持「斜线」和「直线」,可能会导致穿墙。
# 其他描述
- 障碍物用「蓝色」表示
- 可行走点用「灰色」表示
- 起点用「绿色」表示
- 终点用「红色」表示
- 曾经加入
open_map的节点用「深蓝色」表示 close_map的节点用「黄色」表示- 最终路线用「黑色」表示
下图为 A* 算法所得到的寻路图
# JPS 算法
介绍完 A* 算法,接下来就要讲讲本期的「主角」—— JPS 算法。
# 基本概念
JPS 算法是基于 A* 算法实现的基于「跳点」的快速寻路算法,因此在 A* 算法的基础上引入了以下几个规则:
- 强迫邻居(Forced Neighbour)
- 跳点(Jump Point)
# 引言
在介绍这两个规则之前,先简单说明以下 JPS 算法的搜索规则:
JPS 的查询不像 A* 一样,每次查找周围 8 个节点,而是引入了两个概念:
- 进入方向(enter_d)
- 查询方向(find_d)
这里只简单的介绍以下,在后续进行详细讲解
JPS 算法的起点查询时会想周围的 8 个方向进行延展,其中的查询可分为两种
- 直线查询
- 斜线查询
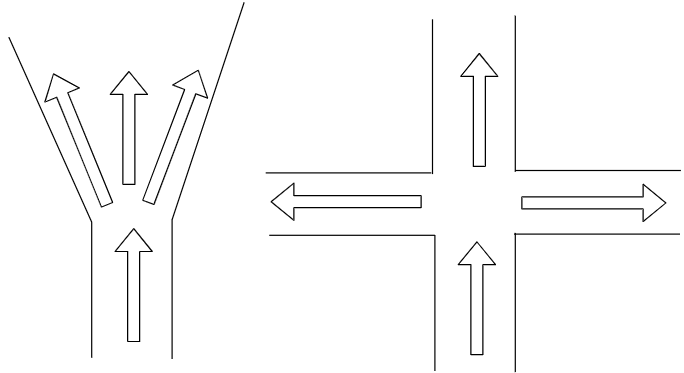
# 直线查询
如果从父节点到当前点的方向是直线,那么该点后续的查询方向只能是直线
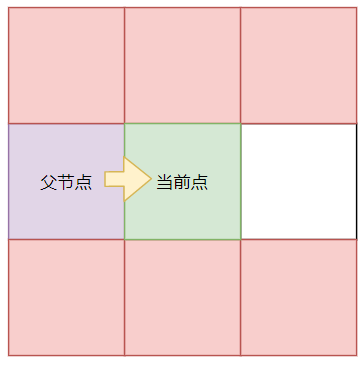
原因也很简单:如果「父节点」可以不通过「当前点」到达红色方格且耗费的路程不会更多,那么就不会选择经过「当前点」到的红色方格,
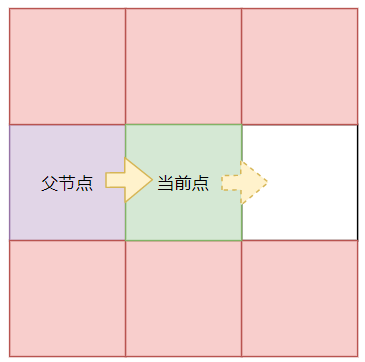
# 斜线查询
如果从父节点到当前点的方向是斜线,那么该点后续的查询方向可以是该方向和其水平 + 垂直方向。
原因和上面的直线查询类似
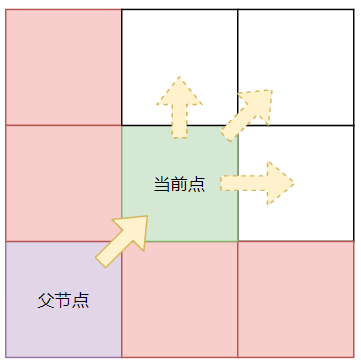
但凡是都有例外,这个例外,我们下面再聊~
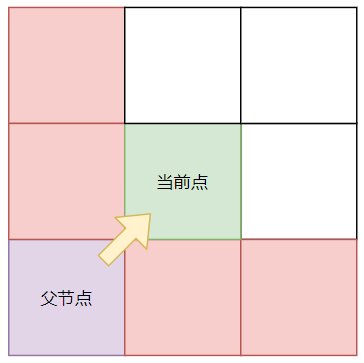
# 强迫邻居
接着上面的查询,让我们再来聊聊这里的例外:
强迫邻居的定义:节点 x 的 8 个邻居中有障碍,且 x 的父节点 p 经过 x 到达 n 的距离代价比不经过 x 到达的 n 的任意路径的距离代价小,则称 n 是 x 的强迫邻居
简单理解可以用两张图来表示:
eg1:假设「起点」到「终点」是直线运动(↑↓←→)。那么强迫邻居有且只能有如下情况:
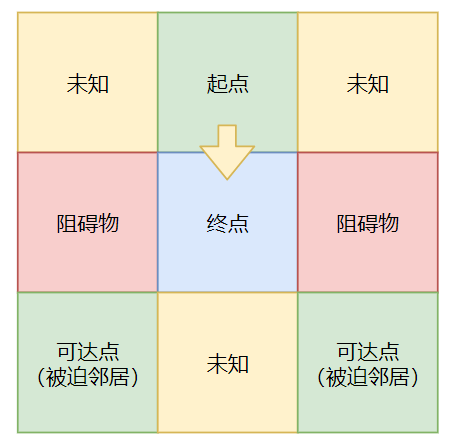
eg2:假设「起点」到「终点」是斜线运动(↖↙↗↘)。那么被迫邻居有且只能有如下情况:
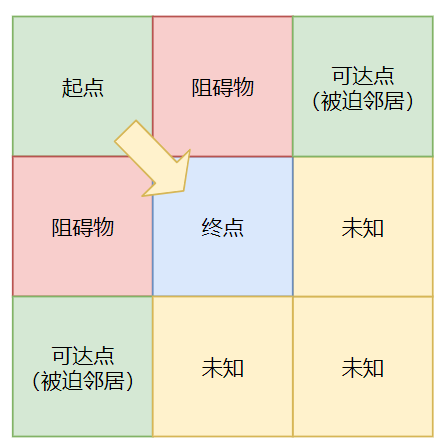
该情况下,由于阻碍物的存在,使得之前的红色格子变成了「最优的路径」,导致其成为「强迫邻居」
那么强迫邻居的意义何在呢,我们接下来再揭晓~
# 跳点
同样,跳点也有如下定义:
- 是「起点」或者「终点」
- 或者周围 8 格内有「强迫邻居」
是的,「强迫邻居」可以用来确定一个点是否为跳点,但这并非其全部左右,预知后续如何,请往下看~
# 间接跳点
以上两个定义满足其一,便可以确定一个点是跳点,除此以外,还有一个比较有趣的定义:
如果该点的进入方向是斜向的。那么沿着它的进入方向的 「水平」和「垂直」 分量进行搜索,并且不遇到障碍物之前能够检索到跳点,那么该点便是「间接跳点」。
间接跳点的作用也很简单,为了能够让地图上的跳点之前能够互相「连通」,所引入的中转站。
至此,
JPS算法的基本概念就算是介绍完毕了,下面将开始讲解其算法过程
# 算法过程
起点加入 open_map | |
起点加入 p_queue | |
while p_queue 不为空: | |
弹出优先级最高的节点 | |
查询该点的后续所有跳点 | |
如果已经在 open_map 中,更新父节点和距离 | |
如果在 close_map 中,跳过 | |
否则直接加入 open_map | |
遇到终点终止循环 |
# 核心思想
该算法的核心就在于「查询方向」和「查询规则」,这两点也是大部分 JPS 变种算法的核心。
# 查询方向
JPS 算法中之前就提到过两个方向: enter_d , find_d
其中 enter_d 方向会决定一个点是否是「跳点」。因为进入方向会决定其周围是否有「强迫邻居」
此外 find_d 也会影响一个点是否是「间接跳点」。因为查询方向上如果存在「跳点」,那么该点也是「跳点」
enter_d 很好理解,就是父节点移动到当前节点的方向。但是 find_d 如何确定呢?
这里又不得不提到之前讨论过的「强迫邻居」的作用。是的,「强迫邻居」可以影响查询方向。
那么事不宜迟,来看看「强迫邻居」是如何影响 find_d 的吧~
上文我们已经提到了两种不同形式的「强迫邻居」,而他们对于 find_d 的影响如下图:
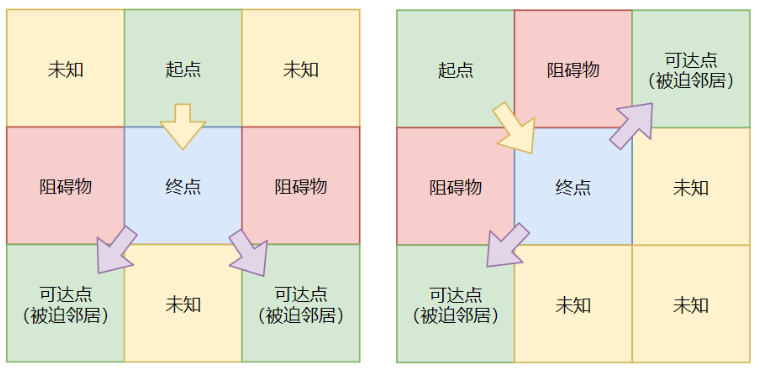
「起点」 -> 「终点」后,「终点」附近存在「强迫邻居」,「强迫邻居」便会引导终点的查询。
论文中使用了较长的篇幅来讲解这样引导后的结果会趋于最优,有兴趣的小伙伴可以看看论文,这里就不做证明。
不过还一个纯个人的理解:
通过跳点进行「延展」,这样才能在保证能够全面的查询到所有点。
题外话就到此,现在~接着 find_d ,继续说明「查询规则」
# 查询规则
由于「起点」本身是没有 enter_d 的,所以其查询方向将会是「四面八方」
其他节点由于有 enter_d ,因此可以通过 enter_d 和「强迫邻居」方向来确定「查询方向」
接着就是沿着该方向进行查询了~
上文之前有简单提及查询规则「直线查询」和「斜线查询」。
此外 JPS 查询还遵循以下规则:
- 直线优于斜线,即:先进行直线的查询,在对斜线进行查询
- 在没有遇到障碍物的情况下,查询不会终止。
因此,基于以上规则,可以画出一个简单的查询示意图:
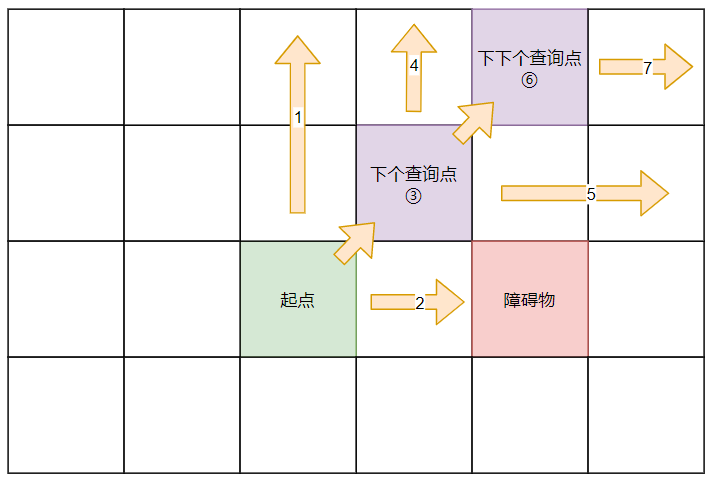
# 梳理思路
经过以上说明,让我们简单整理以下思绪:
- 首先,从起点开始进行「四面八方」查询。
- 通过
enter_d可以判断一个点周围有没有「强迫邻居」 - 如果该点的进入方向是斜线,还需要查看水平和垂直分量上是否有「跳点」
- 把过程中搜索到的的跳点会加入
open_map。 - 跳点的
enter_d会修改后续的find_d,并继续查询,这一步是递归的。 - 遇到障碍物停止查询。
- 通过
至此,完整的查询步骤就介绍完了,接下来,让我们看看查询的结果图吧
# JPS 寻路图

以为这就完了,我们的征途可是是星辰大海!~
# JPS + 算法
JPS+ 是基于 JPS 进行的预处理改良版本,该版本的预处理操作可以极大提高程序运行过程中,查询跳点的消耗。
事不宜迟,让我们接着往下看:
# 前言
由于这部分的论文介绍较少,且和本文的实现有些出入,以下仅供参考,有些不对的地方还请见谅。
# 核心思想
由于查询跳点的操作是依赖于 enter_d 的。换句话说:如果能够存储 8 个方位的每种情况,理论上,是不需要在运行时的去动态判断跳点的。
那么如果可以获取到所有跳点,并把每个点移动到下一个跳点的距离记录下来,就可以干掉运行过程中的查询开销。
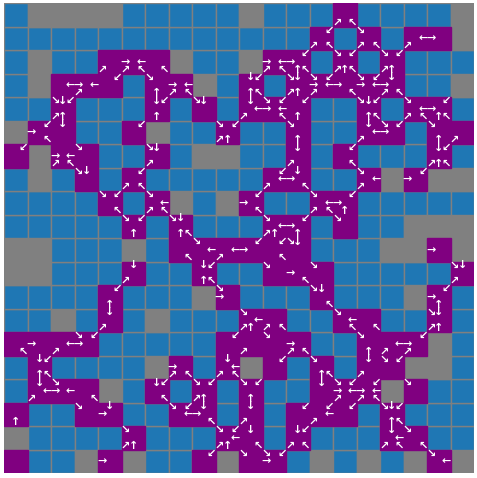
# 跳点预处理
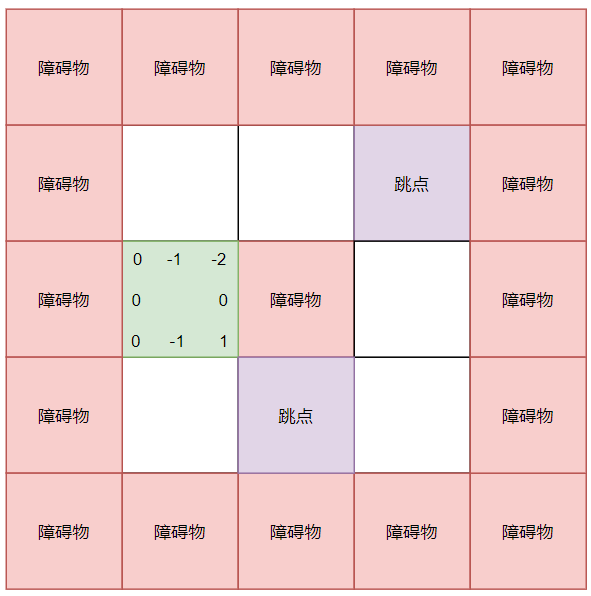
所以可以对地图上每个点的八个进入方向进行跳点判断,并把能够视为跳点的进入方向记录下来,就像这样:
紫色的方块都表示跳点,白色箭头表示的是特定的 enter_d 。
这里把从障碍物移动到目标点的方向给忽略了,因为这些方向是不可能到的目标点的,所以这些 enter_d 也是不存在的。

有了 enter_d ,那么 find_d 的标识岂不信手拈来~
这里没有对 find_d 的方向进行可行性判断,因为在后续的查询中中断,但是会有一定的性能影响。

# 间接跳点预处理
由于除了进入方向可以确定跳点,以下两种情况下也能确定跳点。因此还需要找出间接的跳点!!!
- 起点、终点
- 斜向查询的水平垂直方向存在跳点
处理方法和 JPS 的查询方式比较类似,这里就不过多介绍,处理完成后的结果图:

# 标识距离
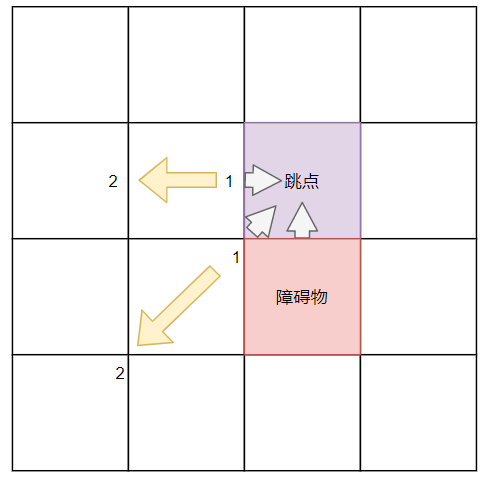
在获得了所有的跳点(起点终点后续再说~),接下来就是处理每个点的距离标识了。
这里我们对每个跳点的 end_d 进行反向查询,这里的斜向插叙不需要拆分,直接斜着查询即可
查询过程中,记录下每个点距离跳点的距离和方向,如果中途遇到了其他跳点,更新它们的距离并停止查询。
此外,为了能够搜索到边界,需要记录每个格子到阻碍物的距离,从 0 到 负无穷进行记录。大致效果如下:
经过一番预处理,我们的地图现在长这样了:
由于 0 太多了,所以距离为 0 的方向就没有标明出来了~

# 算法流程
一切准备工作都已就绪,现在!是时候开始寻路了~
由于我们已经知道了所有的点到边界和下一个跳点的距离。所以查询可以替换一下:
- 起点加入 open_map 和优先队列 | |
- 从优先队列弹出一个优先级最高的节点 | |
- 查看该点的 8 个方向缓存的数据。 | |
- 如果距离 > 0,那么直接把该距离处的点加入 open_map | |
- 如果距离 < 0,对那个点进行一次跳点判断,如果是跳点,加入 open_map | |
- 遇到终点循环终止 |
这下,整个算法中最复杂的地方「查询跳点」就被干掉了,这将大大提高运行效率,因为「查询跳点」本身是递归的~
# JPS+ 寻路图

# 起点和终点
笔者对于「起点」和「终点」做了一些思考。由于这两个点也是「跳点」,所以按理也需要在预处理过程中更新地图的缓存距离。
但是缓存数据本身就是固定的,每次设置不同的起点和终点,都要修改缓存数据并且还原,这种方式确实不够高效。
单独存储一个额外数据用于起点和终点的特殊处理也不失为一个办法。
但是目前还没有找到最为合适的解决办法,也算是一个思维扩展吧,其他小伙伴可以思考其他解决思路。
# 性能分析
说了这么多,那么 JPS 到底有没有那么「快」呢?让我们来做一个性能测试康康 (ง・_・)ง
测试使用的是 20 X 20 的网格。
其中「总遍历节点」是「open_map」+「close_map」的节点数量
| A * 用时 | JPS | JPS+ | A * 总遍历节点 | JPS | JPS+ | A * 路线长度 | JPS | JPS+ | 障碍物占比 |
|---|---|---|---|---|---|---|---|---|---|
| 16.806s | 24.399s | 11.382s | 173 | 155 | 112 | 35.213 | 35.213 | 35.213 | 50% 占比(有路线) |
| 16.443s | 36.007s | 14.571s | 204 | 226 | 180 | 30.627 | 30.627 | 30.384 | 33% 占比(有路线) |
| 14.013s | 44.621s | 8.236s | 196 | 254 | 105 | 28.627 | 28.627 | 28.627 | 20% 占比(有路线) |
| 8.767s | 24.259s | 0.285s | 131 | 3 | 3 | 26.870 | 26.870 | 26.870 | 0% 占比(有路线) |
| 39.636s | 57.200s | 24.762s | 398 | 297 | 264 | 无 | 无 | 无 | 50% 占比(无路线) |
总体来说
JPS+ > A* > JPS
# Why?
为什么 JPS 看起来更「慢」了?
这个问题确实引人深思,笔者自己给出的几个解释:
- 由于测试代码是 python 实现的。对于 A* 算法进行优化的查询主要是解决大量节点加入和移除优先队列导致的性能问题。但是 python 本身的运行效果就不是很高,因此会出现其他地方成为性能热点,从而 JPS 的性能提升不太明显。
- 由于测试地图是全随机地形,所以障碍物的分布比较「均匀」且「零散」,这将导致「跳点」的数量暴增!!!,反而会降低搜索效率。
- 当然还有一种可能,就是笔者代码写的有问题 (#`-_ゝ -),其他小伙伴有兴趣可以试试。
另外一个值得关注的地方就是在 「0% 占比(有路线)」情况下, JPS+ 的性能异常优越!,于是看了以下该情况下的寻路图:
A*
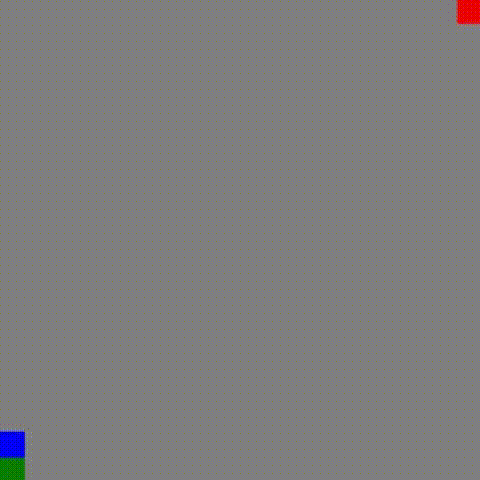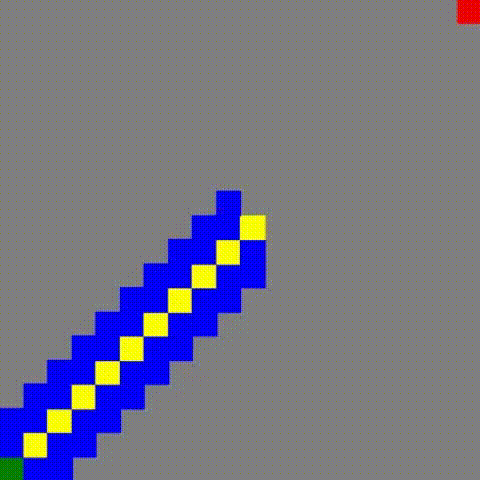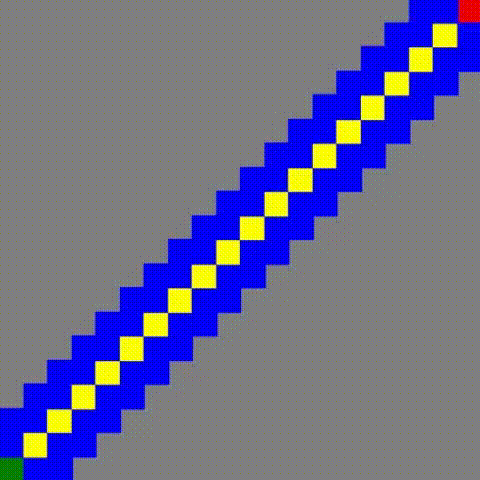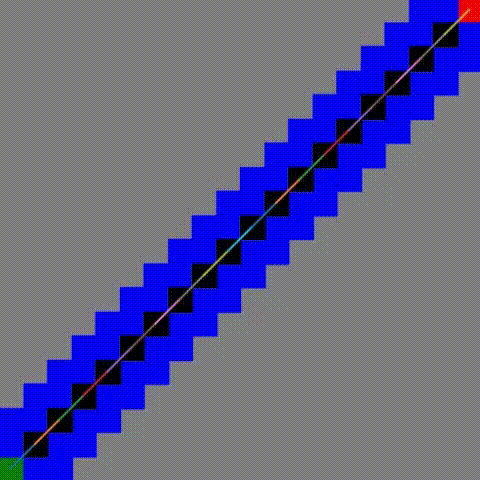
JPS+

这里顺带一提, JPS 和 JPS+ 的寻路图是一样的,但是 JPS 耗时却用了 24s 多。
原因是 JPS+ 的查询方式导致了每次到达终点都等同于遍历了一遍全图~
# 参考资料
A* search algorithm - Wikipedia
路径规划之 A* 算法
JPS 论文原文 (anu.edu.au)
JPS/JPS+ 寻路算法 - KillerAery - 博客园
JPS-Over-100x-Faster-than
跳点搜索算法 (JPS 算法) && 效率优化 (摘录)
最快速的寻路算法 Jump Point Search - 知乎